8.3: The Observed Significance of a Test
- Page ID
- 521
- To learn what the observed significance of a test is.
- To learn how to compute the observed significance of a test.
- To learn how to apply the \(p\)-value approach to hypothesis testing.
The Observed Significance
The conceptual basis of our testing procedure is that we reject \(H_0\) only if the data that we obtained would constitute a rare event if \(H_0\) were actually true. The level of significance α specifies what is meant by “rare.” The observed significance of the test is a measure of how rare the value of the test statistic that we have just observed would be if the null hypothesis were true. That is, the observed significance of the test just performed is the probability that, if the test were repeated with a new sample, the result of the new test would be at least as contrary to \(H_0\) and in support of \(H_a\) as what was observed in the original test.
The observed significance or \(p\)-value of a specific test of hypotheses is the probability, on the supposition that \(H_0\) is true, of obtaining a result at least as contrary to \(H_0\) and in favor of \(H_a\) as the result actually observed in the sample data.
Think back to "Example 8.2.1", Section 8.2 concerning the effectiveness of a new pain reliever. This was a left-tailed test in which the value of the test statistic was \(-1.886\). To be as contrary to \(H_0\) and in support of \(H_a\) as the result \(Z=-1.886\) actually observed means to obtain a value of the test statistic in the interval \((-\infty ,-1.886]\). Rounding \(-1.886\) to \(-1.89\), we can read directly from Figure 7.1.5 that \(P(Z\leq -1.89)=0.0294\). Thus the \(p\)-value or observed significance of the test in "Example 8.2.1", Section 8.2 is \(0.0294\) or about \(3\%\). Under repeated sampling from this population, if \(H_0\) were true then only about \(3\%\) of all samples of size \(50\) would give a result as contrary to \(H_0\) and in favor of \(H_a\) as the sample we observed. Note that the probability \(0.0294\) is the area of the left tail cut off by the test statistic in this left-tailed test.
Analogous reasoning applies to a right-tailed or a two-tailed test, except that in the case of a two-tailed test being as far from \(0\) as the observed value of the test statistic but on the opposite side of \(0\) is just as contrary to \(H_0\) as being the same distance away and on the same side of \(0\), hence the corresponding tail area is doubled.
Computational Definition of the Observed Significance of a Test of Hypotheses
The observed significance of a test of hypotheses is the area of the tail of the distribution cut off by the test statistic (times two in the case of a two-tailed test).
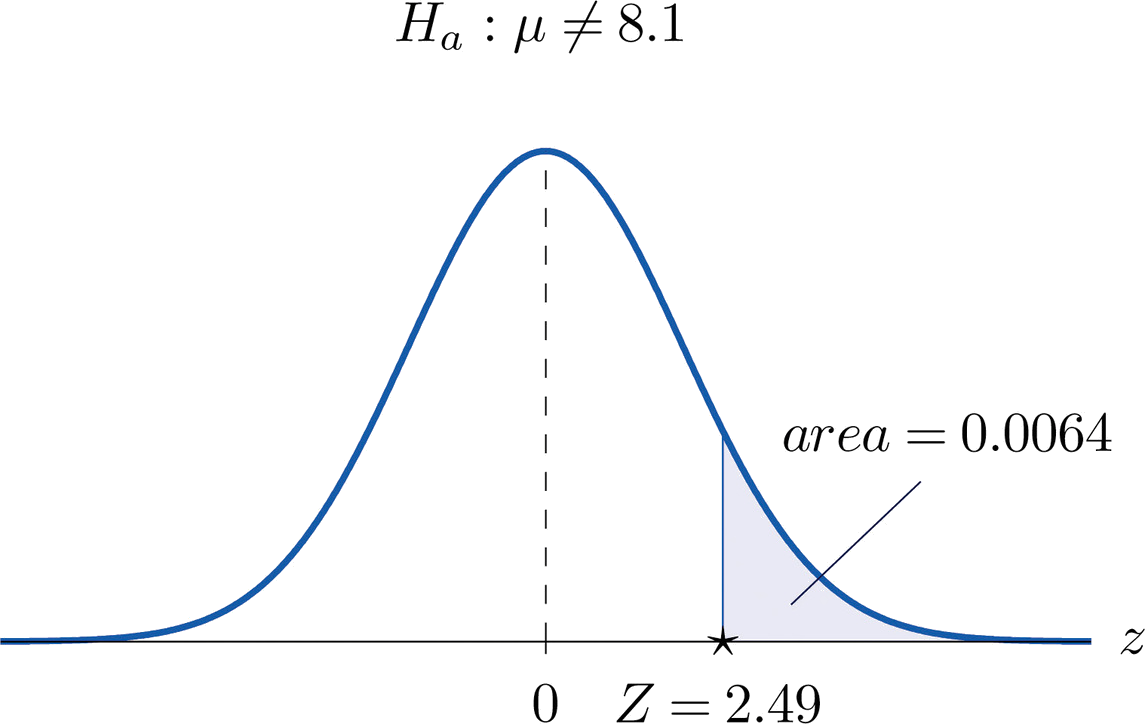
Compute the observed significance of the test performed in "Example 8.2.2", Section 8.2.
Solution
The value of the test statistic was \(z=2.490\), which by Figure 7.1.5 cuts off a tail of area \(0.0064\), as shown in Figure \(\PageIndex{1}\). Since the test was two-tailed, the observed significance is \(2\times 0.0064=0.0128\).
The p-value Approach to Hypothesis Testing
In "Example 8.2.1", Section 8.2 the test was performed at the \(5\%\) level of significance: the definition of “rare” event was probability \(\alpha =0.05\) or less. We saw above that the observed significance of the test was \(p=0.0294\) or about \(3\%\). Since \(p=0.0294<0.05=\alpha\) (or \(3\%\) is less than \(5\%\)), the decision turned out to be to reject: what was observed was sufficiently unlikely to qualify as an event so rare as to be regarded as (practically) incompatible with \(H_0\).
In "Example 8.2.2", Section 8.2 the test was performed at the \(1\%\) level of significance: the definition of “rare” event was probability \(\alpha =0.01\) or less. The observed significance of the test was computed in "Example \(\PageIndex{1}\)" as \(p=0.0128\) or about \(1.3\%\). Since \(p=0.0128>0.01=\alpha\) (or \(1.3\%\) is greater than \(1\%\)), the decision turned out to be not to reject. The event observed was unlikely, but not sufficiently unlikely to lead to rejection of the null hypothesis.
The reasoning just presented is the basis for a slightly different but equivalent formulation of the hypothesis testing process. The first three steps are the same as before, but instead of using \(\alpha\) to compute critical values and construct a rejection region, one computes the \(p\)-value \(p\) of the test and compares it to \(\alpha\), rejecting \(H_0\) if \(p\leq \alpha\) and not rejecting if \(p>\alpha\).
Systematic Hypothesis Testing Procedure: p-Value Approach
- Identify the null and alternative hypotheses.
- Identify the relevant test statistic and its distribution.
- Compute from the data the value of the test statistic.
- Compute the \(p\)-value of the test.
- Compare the value computed in Step 4 to significance level α and make a decision: reject \(H_0\) if \(p\leq \alpha\) and do not reject \(H_0\) if \(p>\alpha\). Formulate the decision in the context of the problem, if applicable.
The total score in a professional basketball game is the sum of the scores of the two teams. An expert commentator claims that the average total score for NBA games is \(202.5\). A fan suspects that this is an overstatement and that the actual average is less than \(202.5\). He selects a random sample of \(85\) games and obtains a mean total score of \(199.2\) with standard deviation \(19.63\). Determine, at the \(5\%\) level of significance, whether there is sufficient evidence in the sample to reject the expert commentator’s claim.
Solution
- Step 1. Let \(\mu\) be the true average total game score of all NBA games. The relevant test is \[H_0: \mu =202.5\\ \text{vs}\\ H_a: \mu <202.5\; @\; \alpha =0.05 \nonumber \]
- Step 2. The sample is large and the population standard deviation is unknown. Thus the test statistic is \[Z=\frac{\bar{x}-\mu _0}{s/\sqrt{n}} \nonumber \] and has the standard normal distribution.
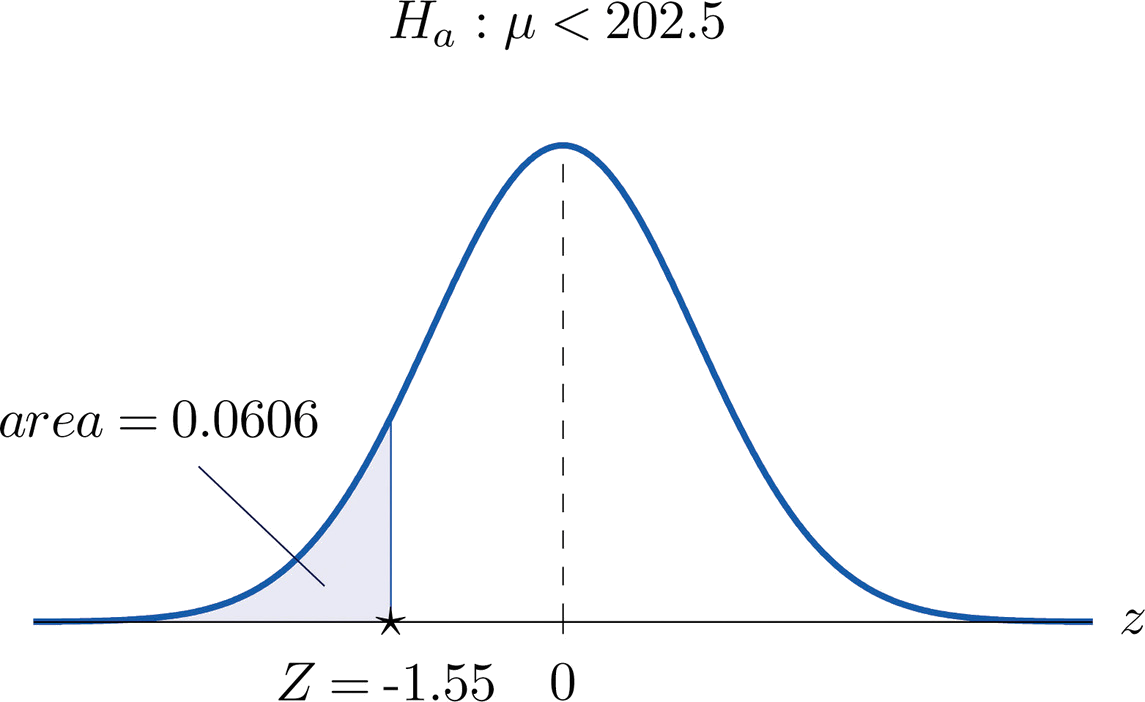
- Step 3. Inserting the data into the formula for the test statistic gives \[Z=\frac{\bar{x}-\mu _0}{s/\sqrt{n}}=\frac{199.2-202.5}{19.63/\sqrt{85}}=-1.55 \nonumber \]
- Step 4. The area of the left tail cut off by \(z=-1.55\) is, by Figure 7.1.5, \(0.0606\), as illustrated in Figure \(\PageIndex{2}\). Since the test is left-tailed, the \(p\)-value is just this number, \(p=0.0606\).
- Step 5. Since \(p=0.0606>0.05=\alpha\), the decision is not to reject \(H_0\). In the context of the problem our conclusion is:
The data do not provide sufficient evidence, at the \(5\%\) level of significance, to conclude that the average total score of NBA games is less than \(202.5\).
Mr. Prospero has been teaching Algebra II from a particular textbook at Remote Isle High School for many years. Over the years students in his Algebra II classes have consistently scored an average of \(67\) on the end of course exam (EOC). This year Mr. Prospero used a new textbook in the hope that the average score on the EOC test would be higher. The average EOC test score of the \(64\) students who took Algebra II from Mr. Prospero this year had mean \(69.4\) and sample standard deviation \(6.1\). Determine whether these data provide sufficient evidence, at the \(1\%\) level of significance, to conclude that the average EOC test score is higher with the new textbook.
Solution
- Step 1. Let \(\mu\) be the true average score on the EOC exam of all Mr. Prospero’s students who take the Algebra II course with the new textbook. The natural statement that would be assumed true unless there were strong evidence to the contrary is that the new book is about the same as the old one. The alternative, which it takes evidence to establish, is that the new book is better, which corresponds to a higher value of \(\mu\). Thus the relevant test is \[H_0: \mu =67\\ \text{vs}\\ H_a: \mu >67\; @\; \alpha =0.01 \nonumber \]
- Step 2. The sample is large and the population standard deviation is unknown. Thus the test statistic is \[Z=\frac{\bar{x}-\mu _0}{s/\sqrt{n}} \nonumber \] and has the standard normal distribution.
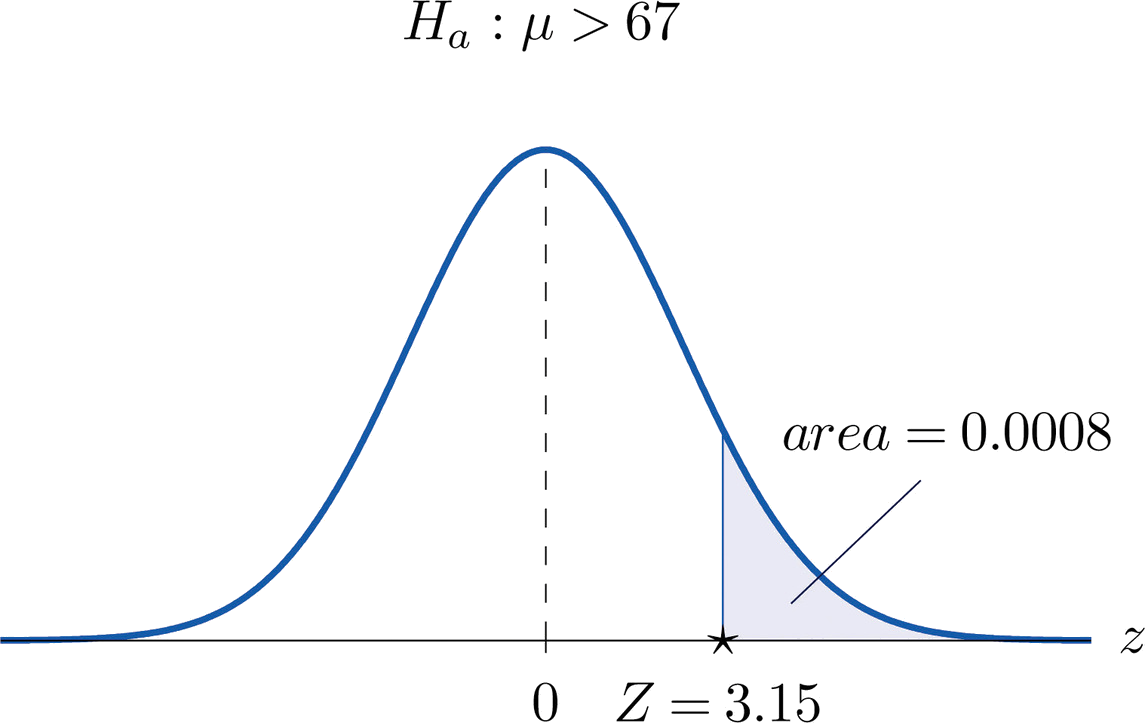
- Step 3. Inserting the data into the formula for the test statistic gives \[Z=\frac{\bar{x}-\mu _0}{s/\sqrt{n}}=\frac{69.4-67}{6.1/\sqrt{64}}=3.15 \nonumber \]
- Step 4. The area of the right tail cut off by \(z=3.15\) is, by Figure 7.1.5, \(1-0.9992=0.0008\), as shown in Figure \(\PageIndex{3}\). Since the test is right-tailed, the \(p\)-value is just this number, \(p=0.0008\).
- Step 5. Since \(p=0.0008<0.01=\alpha\), the decision is to reject \(H_0\). In the context of the problem our conclusion is:
The data provide sufficient evidence, at the \(1\%\) level of significance, to conclude that the average EOC exam score of students taking the Algebra II course from Mr. Prospero using the new book is higher than the average score of those taking the course from him but using the old book.
For the surface water in a particular lake, local environmental scientists would like to maintain an average pH level at \(7.4\). Water samples are routinely collected to monitor the average pH level. If there is evidence of a shift in pH value, in either direction, then remedial action will be taken. On a particular day \(30\) water samples are taken and yield average pH reading of \(7.7\) with sample standard deviation \(0.5\). Determine, at the \(1\%\) level of significance, whether there is sufficient evidence in the sample to indicate that remedial action should be taken.
Solution
- Step 1. Let \(\mu\) be the true average pH level at the time the samples were taken. The relevant test is \[H_0: \mu =7.4\\ \text{vs}\\ H_a: \mu \neq 7.4\; @\; \alpha =0.01 \nonumber \]
- Step 2. The sample is large and the population standard deviation is unknown. Thus the test statistic is \[Z=\frac{\bar{x}-\mu _0}{s/\sqrt{n}} \nonumber \] and has the standard normal distribution.
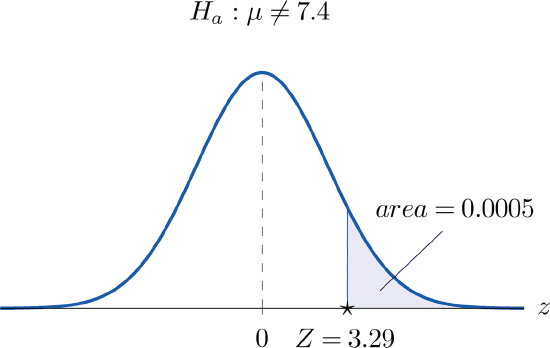
- Step 3. Inserting the data into the formula for the test statistic gives \[Z=\frac{\bar{x}-\mu _0}{s/\sqrt{n}}=\frac{7.7-7.4}{0.5/\sqrt{30}}=3.29 \nonumber \]
- Step 4. The area of the right tail cut off by \(z=3.29\) is, by Figure 7.1.5, \(1-0.9995=0.0005\), as illustrated in Figure \(\PageIndex{4}\). Since the test is two-tailed, the p-value is the double of this number, p=2×0.0005=0.0010.
- Step 5. Since \(p=0.0010<0.01=\alpha\), the decision is to reject \(H_0\). In the context of the problem our conclusion is:
The data provide sufficient evidence, at the \(1\%\) level of significance, to conclude that the average pH of surface water in the lake is different from \(7.4\). That is, remedial action is indicated.
- The observed significance or \(p\)-value of a test is a measure of how inconsistent the sample result is with \(H_0\) and in favor of \(H_a\).
- The \(p\)-value approach to hypothesis testing means that one merely compares the \(p\)-value to \(\alpha\) instead of constructing a rejection region.
- There is a systematic five-step procedure for the \(p\)-value approach to hypothesis testing.


