9.8: Sampling Distribution of p
- Page ID
- 2269
Learning Objectives
- State the relationship between the sampling distribution of p and the normal distribution
Assume that in an election race between \(\text{Candidate A}\) and \(\text{Candidate B}\), \(0.60\) of the voters prefer \(\text{Candidate A}\). If a random sample of \(10\) voters were polled, it is unlikely that exactly \(60\%\) of them (\(6\)) would prefer \(\text{Candidate A}\). By chance the proportion in the sample preferring \(\text{Candidate A}\) could easily be a little lower than \(0.60\) or a little higher than \(0.60\). The sampling distribution of \(p\) is the distribution that would result if you repeatedly sampled \(10\) voters and determined the proportion (\(p\)) that favored \(\text{Candidate A}\).
The sampling distribution of \(p\) is a special case of the sampling distribution of the mean. Table \(\PageIndex{1}\) shows a hypothetical random sample of \(10\) voters. Those who prefer \(\text{Candidate A}\) are given scores of \(1\) and those who prefer \(\text{Candidate B}\) are given scores of \(0\). Note that seven of the voters prefer \(\text{Candidate A}\) so the sample proportion (\(p\)) is
\[p = \frac{7}{10} = 0.70\]
As you can see, \(p\) is the mean of the \(10\) preference scores.
| Voter | Preference |
|---|---|
| 1 | 1 |
| 2 | 0 |
| 3 | 1 |
| 4 | 1 |
| 5 | 1 |
| 6 | 0 |
| 7 | 1 |
| 8 | 0 |
| 9 | 1 |
| 10 | 1 |
The distribution of \(p\) is closely related to the binomial distribution. The binomial distribution is the distribution of the total number of successes (favoring \(\text{Candidate A}\), for example) whereas the distribution of \(p\) is the distribution of the mean number of successes. The mean, of course, is the total divided by the sample size, \(N\). Therefore, the sampling distribution of \(p\) and the binomial distribution differ in that \(p\) is the mean of the scores (\(0.70\)) and the binomial distribution is dealing with the total number of successes (\(7\)).
The binomial distribution has a mean of
\[\mu =N\pi\]
Dividing by \(N\) to adjust for the fact that the sampling distribution of \(p\) is dealing with means instead of totals, we find that the mean of the sampling distribution of \(p\) is:
\[\mu _p=\pi\]
The standard deviation of the binomial distribution is:
\[\sqrt{N\pi(1-\pi )}\]
Dividing by \(N\) because \(p\) is a mean not a total, we find the standard error of \(p\):
\[\sigma _p=\frac{\sqrt{N\pi(1-\pi )}}{N}=\sqrt{\frac{\pi(1-\pi )}{N}}\]
Returning to the voter example, \(\pi =0.60\) and \(N = 10\). (Don't confuse \(\pi =0.60\), the population proportion and \(p = 0.70\), the sample proportion.) Therefore, the mean of the sampling distribution of \(p\) is \(0.60\). The standard error is
\[\sigma _p=\sqrt{\frac{0.60(1-0.60)}{10}}=0.155\]
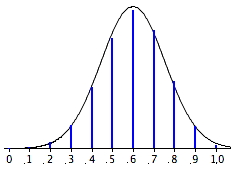
The sampling distribution of \(p\) is a discrete rather than a continuous distribution. For example, with an \(N\) of \(10\), it is possible to have a \(p\) of \(0.50\) or a \(p\) of \(0.60\) but not a \(p\) of \(0.55\).
The sampling distribution of \(p\) is approximately normally distributed if \(N\) is fairly large and \(\pi\) is not close to \(0\) or \(1\). A rule of thumb is that the approximation is good if both \(N\pi\) and \(N(1-\pi )\) are greater than \(10\). The sampling distribution for the voter example is shown in Figure \(\PageIndex{1}\). Note that even though \(N(1-\pi )\) is only \(4\), the approximation is quite good.