9.5: Sampling Distribution of the Mean
- Page ID
- 2135
Learning Objectives
- State the mean and variance of the sampling distribution of the mean
- Compute the standard error of the mean
- State the central limit theorem
The sampling distribution of the mean was defined in the section introducing sampling distributions. This section reviews some important properties of the sampling distribution of the mean introduced in the demonstrations in this chapter.
Sampling Mean
The mean of the sampling distribution of the mean is the mean of the population from which the scores were sampled. Therefore, if a population has a mean \(\mu\), then the mean of the sampling distribution of the mean is also \(\mu\). The symbol \(\mu _M\) is used to refer to the mean of the sampling distribution of the mean. Therefore, the formula for the mean of the sampling distribution of the mean can be written as:
\[\mu _M = \mu\]
Sampling Variance
The variance of the sampling distribution of the mean is computed as follows:
\[ \sigma_M^2 = \dfrac{\sigma^2}{N}\]
That is, the variance of the sampling distribution of the mean is the population variance divided by \(N\), the sample size (the number of scores used to compute a mean). Thus, the larger the sample size, the smaller the variance of the sampling distribution of the mean.
Note
(optional) This expression can be derived very easily from the variance sum law. Let's begin by computing the variance of the sampling distribution of the sum of three numbers sampled from a population with variance \(\sigma ^2\). The variance of the sum would be:
\[\sigma ^2 + \sigma ^2 + \sigma ^2\]
For \(N\) numbers, the variance would be \(N\sigma ^2\). Since the mean is \(1/N\) times the sum, the variance of the sampling distribution of the mean would be \(1/N^2\) times the variance of the sum, which equals \(\sigma ^2/N\).
The standard error of the mean is the standard deviation of the sampling distribution of the mean. It is therefore the square root of the variance of the sampling distribution of the mean and can be written as:
\[ \sigma_M = \dfrac{\sigma}{\sqrt{N}}\]
The standard error is represented by a \(\sigma\) because it is a standard deviation. The subscript (\(M\)) indicates that the standard error in question is the standard error of the mean.
Central Limit Theorem
Definition
The central limit theorem states that:
Given a population with a finite mean \(\mu\) and a finite non-zero variance \(\sigma ^2\), the sampling distribution of the mean approaches a normal distribution with a mean of \(\mu\) and a variance of \(\sigma ^2/N\) as \(N\), the sample size, increases.
The expressions for the mean and variance of the sampling distribution of the mean are not new or remarkable. What is remarkable is that regardless of the shape of the parent population, the sampling distribution of the mean approaches a normal distribution as \(N\) increases. If you have used the "Central Limit Theorem Demo," you have already seen this for yourself. As a reminder, Figure \(\PageIndex{1}\) shows the results of the simulation for \(N = 2\) and \(N = 10\). The parent population was a uniform distribution. You can see that the distribution for \(N = 2\) is far from a normal distribution. Nonetheless, it does show that the scores are denser in the middle than in the tails. For \(N = 10\) the distribution is quite close to a normal distribution. Notice that the means of the two distributions are the same, but that the spread of the distribution for \(N = 10\) is smaller.
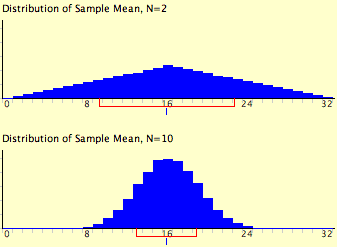
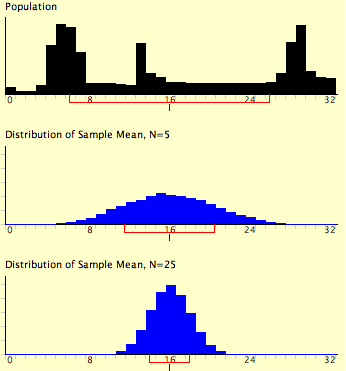
Figure \(\PageIndex{2}\) shows how closely the sampling distribution of the mean approximates a normal distribution even when the parent population is very non-normal. If you look closely you can see that the sampling distributions do have a slight positive skew. The larger the sample size, the closer the sampling distribution of the mean would be to a normal distribution.