2.6: Continuous Distributions
- Page ID
- 327
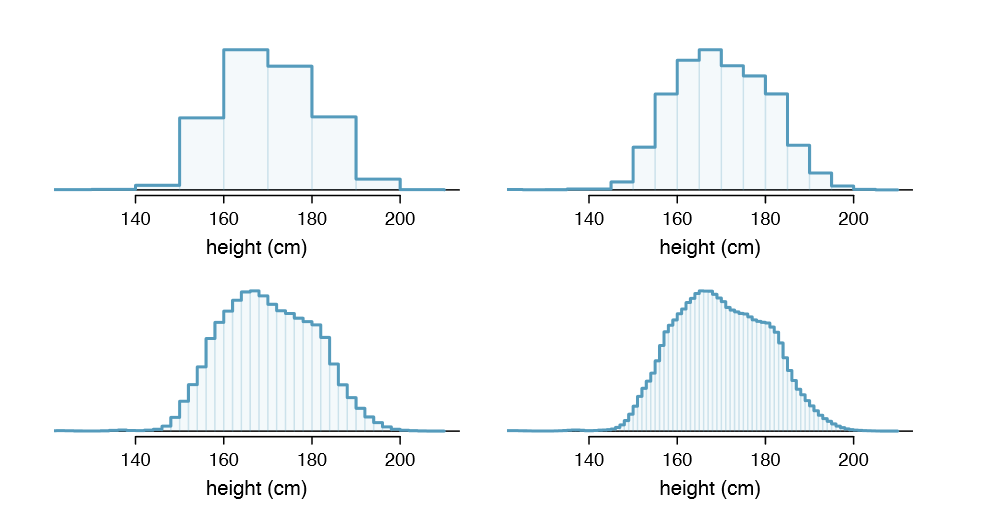
Example 2.88 Figure 2.26 shows a few different hollow histograms of the variable height for 3 million US adults from the mid-90's.58 How does changing the number of bins allow you to make different interpretations of the data?
Adding more bins provides greater detail. This sample is extremely large, which is why much smaller bins still work well. Usually we do not use so many bins with smaller sample sizes since small counts per bin mean the bin heights are very volatile.
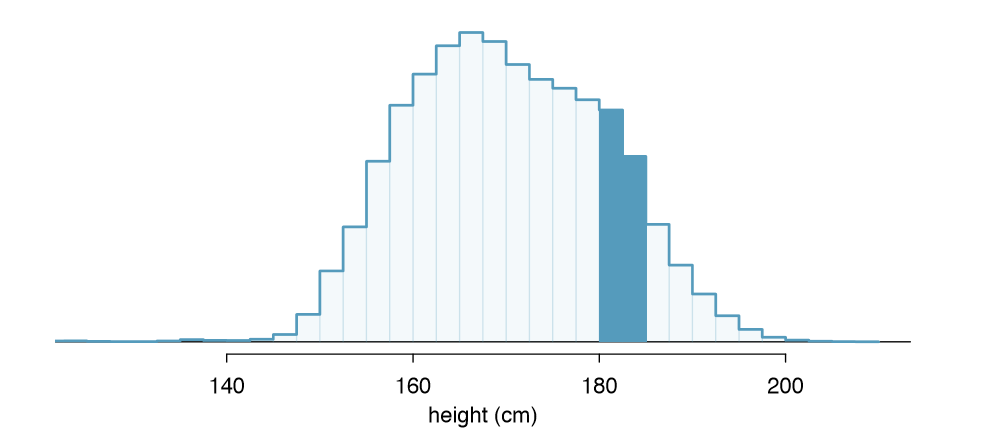
Example 2.89 What proportion of the sample is between 180 cm and 185 cm tall (about 5'11" to 6'1")?
We can add up the heights of the bins in the range 180 cm and 185 and divide by the sample size. For instance, this can be done with the two shaded bins shown in Figure 2.27. The two bins in this region have counts of 195,307 and 156,239 people, resulting in the following estimate of the probability:
\[\frac {195307 + 156239}{3,000,000} = 0.1172\]
This fraction is the same as the proportion of the histogram's area that falls in the range 180 to 185 cm.
58This sample can be considered a simple random sample from the US population. It relies on the USDA Food Commodity Intake Database.
From histograms to continuous distributions
Examine the transition from a boxy hollow histogram in the top-left of Figure 2.26 to the much smoother plot in the lower-right. In this last plot, the bins are so slim that the hollow histogram is starting to resemble a smooth curve. This suggests the population height as a continuous numerical variable might best be explained by a curve that represents the outline of extremely slim bins.
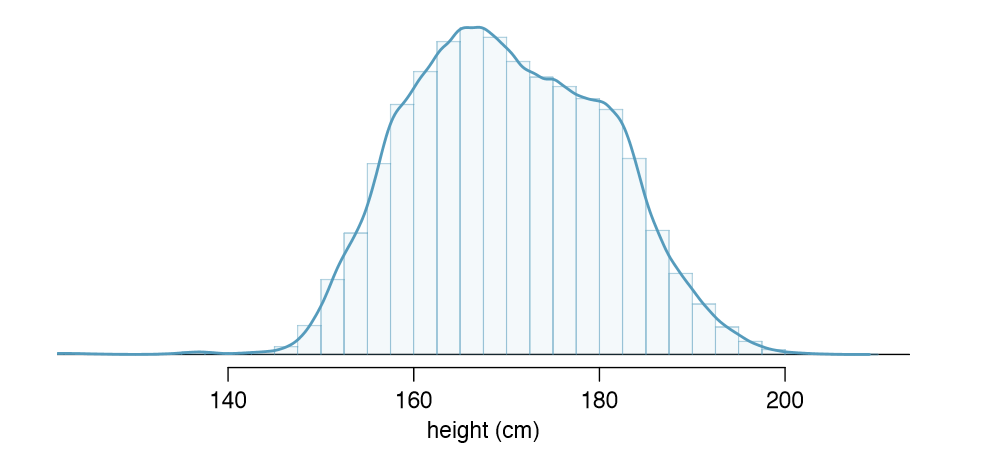
This smooth curve represents a probability density function (also called a density or distribution), and such a curve is shown in Figure 2.28 overlaid on a histogram of the sample. A density has a special property: the total area under the density's curve is 1.
Probabilities from continuous distributions
We computed the proportion of individuals with heights 180 to 185 cm in Example 2.89 as a fraction:
\[\frac {number of people between 180 and 185}{total sample size}\]
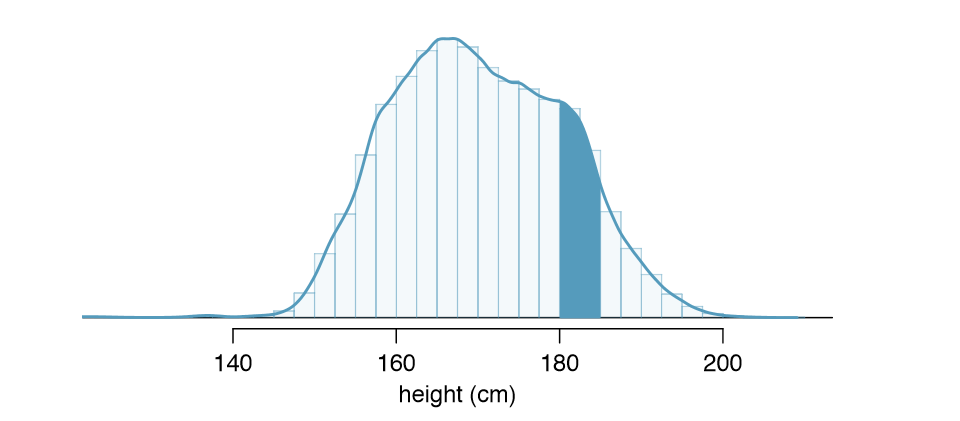
We found the number of people with heights between 180 and 185 cm by determining the fraction of the histogram's area in this region. Similarly, we can use the area in the shaded region under the curve to nd a probability (with the help of a computer):
\[P(height between 180 and 185) = area between 180 and 185 = 0.1157\]
The probability that a randomly selected person is between 180 and 185 cm is 0.1157. This is very close to the estimate from Example 2.89: 0.1172.
Exercise 2.90 Three US adults are randomly selected. The probability a single adult is between 180 and 185 cm is 0.1157.59
(a) What is the probability that all three are between 180 and 185 cm tall?
(b) What is the probability that none are between 180 and 185 cm?
Example 2.91 What is the probability that a randomly selected person is exactly 180 cm? Assume you can measure perfectly.
This probability is zero. A person might be close to 180 cm, but not exactly 180 cm tall. This also makes sense with the de nition of probability as area; there is no area captured between 180 cm and 180 cm.
Exercise 2.92 Suppose a person's height is rounded to the nearest centimeter. Is there a chance that a random person's measured height will be 180 cm?60
59Brief answers: (a) \(0.1157 X 0.1157 X 0.1157 = 0.0015\). (b) \((1 - 0.1157)^3 = 0.692\)
60This has positive probability. Anyone between 179.5 cm and 180.5 cm will have a measured height of 180 cm. This is probably a more realistic scenario to encounter in practice versus Example 2.91.


