3.6: Squared Differences Simulation
- Page ID
- 2094
Learning Objectives
- Learn which measure of central tendency minimizes the sum of squared deviations
Instructions
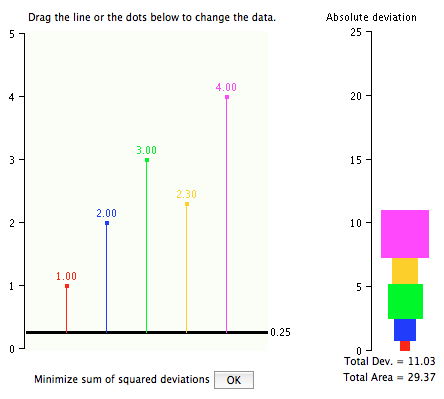
This demonstration allows you to examine the sum of squared deviations from a given value. The graph to the right shows the numbers \(1, 2, 3, 4,\) and \(5\) and their deviations from an arbitrary starting value of \(0.254\) (the figure displays this rounded to \(0.25\)).
The first number, \(1\), is represented by a red dot. The deviation from \(0.254\) is represented by a red line from the red dot to the black line. The value of the black line is \(0.254\).
Similarly, the number \(2\) is represented by a blue dot and its deviation from \(0.25\) is represented by a blue line.
The height of the colored rectangles represents the sum of the absolute deviations from the black line. The sum of the deviations of the numbers \(1, 2, 3, 4,\) and \(5\) from \(0.25\) is \(0.746 + 1.75 + 2.746 + 3.746 + 4.746 = 13.73\).
The area of each rectangle represents the magnitude of the squared deviation of a point from the black line. For example, the red rectangle has an area of \(0.746\times 0.746 = 0.557\). The sum of all the areas of the rectangles is \(47.70\). The sum of all the areas represents the sum of the squared deviations.
In this demonstration, you can move the black bar by clicking on it and dragging it up or down. In the second figure it has been moved up to \(1.0\). The deviation of the red point from the black bar is now \(0\) since they are both \(1\). The sum of the deviations is now \(10 (0 + 1 + 2 + 3 + 4)\) and the sum of squared deviations is \(30 (0^2 + 1^2 + 2^2 + 3^2 + 4^2)\).
As you move the bar up and down, the value of the sum of absolute deviations and the sum of squared deviations changes.
See if you can find the placement of the black bar that produces the smallest value for the sum of the squared deviations.
To check and see if you found the smallest value, click the "OK" button at the bottom of the graph. It will move the bar to the location that produces the smallest sum of squared deviations.
For the initial data, the value that minimizes the sum of squared deviations is also the value that minimizes the sum of absolute deviations. This will not be true for most data.
You can also move the individual points. Click on one of the points and move it up or down and note the effect. Your goal for this demonstration is to discover a rule for determining what value will give you the smallest sum of squared deviations.
Illustrated Instructions
Below is a screen shot of the simulation's beginning screen. The "Total Dev." is the sum of the absolute deviations; the "Total Area" is the sum of the squared deviations.
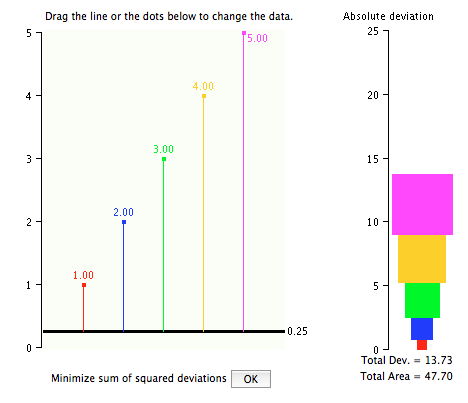
Below is an example after the vertical line has been changed. The distances to the line have been recalculated.
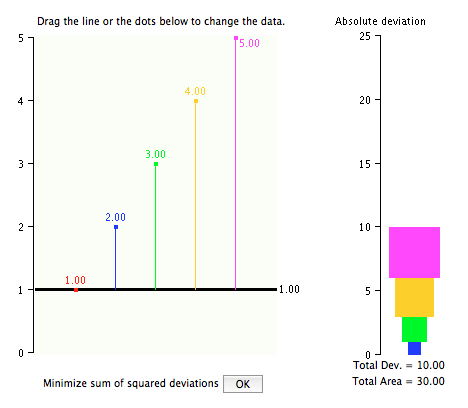
You can change the data by clicking on a data point and dragging. An example with changed data is shown below.