15.3: One-Factor ANOVA
- Page ID
- 2175
Learning Objectives
- State what the Mean Square Between (\(MSB\)) estimates when the null hypothesis is true and when the null hypothesis is false
- Compute \(MSE\)
- Compute \(F\) and its two degrees of freedom parameters
- Explain why ANOVA is best thought of as a two-tailed test even though literally only one tail of the distribution is used
- Partition the sums of squares into condition and error
- Format data to be used with a computer statistics program
This section shows how ANOVA can be used to analyze a one-factor between-subjects design. We will use as our main example the "Smiles and Leniency" case study. In this study there were four conditions with \(34\) subjects in each condition. There was one score per subject. The null hypothesis tested by ANOVA is that the population means for all conditions are the same. This can be expressed as follows:
\[H_0: \mu _1 = \mu _2 = ... = \mu _k\]
where \(H_0\) is the null hypothesis and \(k\) is the number of conditions. In the "Smiles and Leniency" study, \(k = 4\) and the null hypothesis is
\[H_0: \mu _{false} = \mu _{felt} = \mu _{miserable} = \mu _{neutral}\]
If the null hypothesis is rejected, then it can be concluded that at least one of the population means is different from at least one other population mean.
Analysis of variance is a method for testing differences among means by analyzing variance. The test is based on two estimates of the population variance (\(\sigma ^2\)). One estimate is called the mean square error (\(MSE\)) and is based on differences among scores within the groups. \(MSE\) estimates \(\sigma ^2\) regardless of whether the null hypothesis is true (the population means are equal). The second estimate is called the mean square between (\(MSB\)) and is based on differences among the sample means. \(MSB\) only estimates \(\sigma ^2\) if the population means are equal. If the population means are not equal, then \(MSB\) estimates a quantity larger than \(\sigma ^2\). Therefore, if the \(MSB\) is much larger than the \(MSE\), then the population means are unlikely to be equal. On the other hand, if the \(MSB\) is about the same as \(MSE\), then the data are consistent with the null hypothesis that the population means are equal.
Before proceeding with the calculation of \(MSE\) and \(MSB\), it is important to consider the assumptions made by ANOVA:
- The populations have the same variance. This assumption is called the assumption of \(\textit{homogeneity of variance}\).
- The populations are normally distributed.
- Each value is sampled independently from each other value. This assumption requires that each subject provide only one value. If a subject provides two scores, then the values are not independent. The analysis of data with two scores per subject is shown in the section on within-subjects ANOVA later in this chapter.
These assumptions are the same as for a t test of differences between groups except that they apply to two or more groups, not just to two groups.
The means and variances of the four groups in the "Smiles and Leniency" case study are shown in Table \(\PageIndex{1}\). Note that there are \(34\) subjects in each of the four conditions (False, Felt, Miserable, and Neutral).
| Condition | Mean | Variance |
|---|---|---|
| False | 5.3676 | 3.3380 |
| Felt | 4.9118 | 2.8253 |
| Miserable | 4.9118 | 2.1132 |
| Neutral | 4.1176 | 2.3191 |
Sample Sizes
The first calculations in this section all assume that there is an equal number of observations in each group. Unequal sample size calculations are shown here. We will refer to the number of observations in each group as \(n\) and the total number of observations as \(N\). For these data there are four groups of \(34\) observations. Therefore, \(n = 34\) and \(N = 136\).
Computing MSE
Recall that the assumption of homogeneity of variance states that the variance within each of the populations (\(\sigma ^2\)) is the same. This variance, \(\sigma ^2\), is the quantity estimated by \(MSE\) and is computed as the mean of the sample variances. For these data, the \(MSE\) is equal to \(2.6489\).
Computing MSB
The formula for \(MSB\) is based on the fact that the variance of the sampling distribution of the mean is
\[\sigma _{M}^{2}=\frac{\sigma ^2}{n}\]
where \(n\) is the sample size of each group. Rearranging this formula, we have
\[\sigma ^2=n\sigma _{M}^{2}\]
Therefore, if we knew the variance of the sampling distribution of the mean, we could compute \(\sigma ^2\) by multiplying it by \(n\). Although we do not know the variance of the sampling distribution of the mean, we can estimate it with the variance of the sample means. For the leniency data, the variance of the four sample means is \(0.270\). To estimate \(\sigma ^2\), we multiply the variance of the sample means (\(0.270\)) by \(n\) (the number of observations in each group, which is \(34\)). We find that \(MSB = 9.179\).
To sum up these steps:
- Compute the means.
- Compute the variance of the means.
- Multiply the variance of the means by \(n\).
Recap
If the population means are equal, then both \(MSE\) and \(MSB\) are estimates of \(\sigma ^2\) and should therefore be about the same. Naturally, they will not be exactly the same since they are just estimates and are based on different aspects of the data: The \(MSB\) is computed from the sample means and the \(MSE\) is computed from the sample variances.
If the population means are not equal, then \(MSE\) will still estimate \(\sigma ^2\) because differences in population means do not affect variances. However, differences in population means affect \(MSB\) since differences among population means are associated with differences among sample means. It follows that the larger the differences among sample means, the larger the \(MSB\).
Note
In short, \(MSE\) estimates \(\sigma ^2\) whether or not the population means are equal, whereas \(MSB\) estimates \(\sigma ^2\) only when the population means are equal and estimates a larger quantity when they are not equal.
Comparing MSE and MSB
The critical step in an ANOVA is comparing \(MSE\) and \(MSB\). Since \(MSB\) estimates a larger quantity than \(MSE\) only when the population means are not equal, a finding of a larger \(MSB\) than an \(MSE\) is a sign that the population means are not equal. But since \(MSB\) could be larger than \(MSE\) by chance even if the population means are equal, \(MSB\) must be much larger than \(MSE\) in order to justify the conclusion that the population means differ. But how much larger must \(MSB\) be? For the "Smiles and Leniency" data, the \(MSB\) and \(MSE\) are \(9.179\) and \(2.649\), respectively. Is that difference big enough? To answer, we would need to know the probability of getting that big a difference or a bigger difference if the population means were all equal. The mathematics necessary to answer this question were worked out by the statistician R. Fisher. Although Fisher's original formulation took a slightly different form, the standard method for determining the probability is based on the ratio of \(MSB\) to \(MSE\). This ratio is named after Fisher and is called the \(F\) ratio.
For these data, the \(F\) ratio is
\[F = \frac{9.179}{2.649} = 3.465\]
Therefore, the \(MSB\) is \(3.465\) times higher than \(MSE\). Would this have been likely to happen if all the population means were equal? That depends on the sample size. With a small sample size, it would not be too surprising because results from small samples are unstable. However, with a very large sample, the \(MSB\) and \(MSE\) are almost always about the same, and an \(F\) ratio of \(3.465\) or larger would be very unusual. Figure \(\PageIndex{1}\) shows the sampling distribution of \(F\) for the sample size in the "Smiles and Leniency" study. As you can see, it has a positive skew.
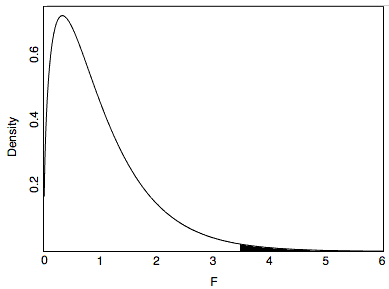
From Figure \(\PageIndex{1}\), you can see that \(F\) ratios of \(3.465\) or above are unusual occurrences. The area to the right of \(3.465\) represents the probability of an \(F\) that large or larger and is equal to \(0.018\). In other words, given the null hypothesis that all the population means are equal, the probability value is \(0.018\) and therefore the null hypothesis can be rejected. The conclusion that at least one of the population means is different from at least one of the others is justified.
The shape of the \(F\) distribution depends on the sample size. More precisely, it depends on two degrees of freedom (\(df\)) parameters: one for the numerator (\(MSB\)) and one for the denominator (\(MSE\)). Recall that the degrees of freedom for an estimate of variance is equal to the number of observations minus one. Since the \(MSB\) is the variance of \(k\) means, it has \(k - 1\) \(df\). The \(MSE\) is an average of \(k\) variances, each with \(n - 1\) \(df\). Therefore, the \(df\) for \(MSE\) is \(k(n - 1) = N - k\), where \(N\) is the total number of observations, \(n\) is the number of observations in each group, and \(k\) is the number of groups. To summarize:
\[df_{numerator} = k-1\]
\[df_{denominator} = N-k\]
For the "Smiles and Leniency" data,
\[df_{numerator} = k-1=4-1=3\]
\[df_{denominator} = N-k=136-4=132\]
\(F = 3.465\)
The \(F\) distribution calculator shows that \(p = 0.018\).
F Calculator
One-Tailed or Two?
Is the probability value from an \(F\) ratio a one-tailed or a two-tailed probability? In the literal sense, it is a one-tailed probability since, as you can see in Figure \(\PageIndex{1}\), the probability is the area in the right-hand tail of the distribution. However, the \(F\) ratio is sensitive to any pattern of differences among means. It is, therefore, a test of a two-tailed hypothesis and is best considered a two-tailed test.
Relationship to the \(t\) test
Since an ANOVA and an independent-groups \(t\) test can both test the difference between two means, you might be wondering which one to use. Fortunately, it does not matter since the results will always be the same. When there are only two groups, the following relationship between \(F\) and \(t\) will always hold:
\[F(1,dfd) = t^2(df)\]
where \(dfd\) is the degrees of freedom for the denominator of the \(F\) test and \(df\) is the degrees of freedom for the \(t\) test. \(dfd\) will always equal \(df\).
Sources of Variation
Why do scores in an experiment differ from one another? Consider the scores of two subjects in the "Smiles and Leniency" study: one from the "False Smile" condition and one from the "Felt Smile" condition. An obvious possible reason that the scores could differ is that the subjects were treated differently (they were in different conditions and saw different stimuli). A second reason is that the two subjects may have differed with regard to their tendency to judge people leniently. A third is that, perhaps, one of the subjects was in a bad mood after receiving a low grade on a test. You can imagine that there are innumerable other reasons why the scores of the two subjects could differ. All of these reasons except the first (subjects were treated differently) are possibilities that were not under experimental investigation and, therefore, all of the differences (variation) due to these possibilities are unexplained. It is traditional to call unexplained variance error even though there is no implication that an error was made. Therefore, the variation in this experiment can be thought of as being either variation due to the condition the subject was in or due to error (the sum total of all reasons the subjects' scores could differ that were not measured).
One of the important characteristics of ANOVA is that it partitions the variation into its various sources. In ANOVA, the term sum of squares (\(SSQ\)) is used to indicate variation. The total variation is defined as the sum of squared differences between each score and the mean of all subjects. The mean of all subjects is called the grand mean and is designated as GM. (When there is an equal number of subjects in each condition, the grand mean is the mean of the condition means.) The total sum of squares is defined as
\[SSQ_{total}=\sum (X-GM)^2\]
which means to take each score, subtract the grand mean from it, square the difference, and then sum up these squared values. For the "Smiles and Leniency" study, \(SSQ_{total}=377.19\).
The sum of squares condition is calculated as shown below.
\[SSQ_{condition}=n\left [ (M_1-GM)^2 + (M_2-GM)^2 + \cdots +(M_k-GM)^2 \right ]\]
where \(n\) is the number of scores in each group, \(k\) is the number of groups, \(M_1\) is the mean for \(\text{Condition 1}\), \(M_2\) is the mean for \(\text{Condition 2}\), and \(M_k\) is the mean for \(\text{Condition k}\). For the Smiles and Leniency study, the values are:
\[\begin{align*} SSQ_{condition} &= 34\left [ (5.37-4.83)^2 + (4.91-4.83)^2 + (4.91-4.83)^2 + (4.12-4.83)^2\right ]\\ &= 27.5 \end{align*}\]
If there are unequal sample sizes, the only change is that the following formula is used for the sum of squares condition:
\[SSQ_{condition}=n_1(M_1-GM)^2 + n_2(M_2-GM)^2 + \cdots + n_k(M_k-GM)^2\]
where \(n_i\) is the sample size of the \(i^{th}\) condition. \(SSQ_{total}\) is computed the same way as shown above.
The sum of squares error is the sum of the squared deviations of each score from its group mean. This can be written as
\[SSQ_{error}=\sum (X_{i1}-M_1)^2 + \sum (X_{i2}-M_2)^2 + \cdots + \sum (X_{ik}-M_k)^2\]
where \(X_{i1}\) is the \(i^{th}\) score in \(\text{group 1}\) and \(M_1\) is the mean for \(\text{group 1}\), \(X_{i2}\) is the \(i^{th}\) score in \(\text{group 2}\) and \(M_2\) is the mean for \(\text{group 2}\), etc. For the "Smiles and Leniency" study, the means are: \(5.368\), \(4.912\), \(4.912\), and \(4.118\). The \(SSQ_{error}\) is therefore:
\[\begin{align*} SSQ_{error} &= (2.5-5.368)^2 + (5.5-5.368)^2 + ... + (6.5-4.118)^2\\ &= 349.65 \end{align*}\]
The sum of squares error can also be computed by subtraction:
\[SSQ_{error} = SSQ_{total} - SSQ_{condition}\]
\[\begin{align*} SSQ_{error} &= 377.189 - 27.535\\ &= 349.65 \end{align*}\]
Therefore, the total sum of squares of \(377.19\) can be partitioned into \(SSQ_{condition}(27.53)\) and \(SSQ_{error} (349.66)\).
Once the sums of squares have been computed, the mean squares (\(MSB\) and \(MSE\)) can be computed easily. The formulas are:
\[MSB = \frac{SSQ_{condition}}{dfn}\]
where \(dfn\) is the degrees of freedom numerator and is equal to \(k - 1 = 3\).
\[MSB = \frac{27.535}{3}=9.18\]
which is the same value of \(MSB\) obtained previously (except for rounding error). Similarly,
\[MSE = \frac{SSQ_{error}}{dfd}\]
where \(dfd\) is the degrees of freedom for the denominator and is equal to \(N - k\).
\(dfd = 136 - 4 = 132\)
\(MSE = 349.66/132 = 2.65\)
which is the same as obtained previously (except for rounding error). Note that the \(dfd\) is often called the \(dfe\) for degrees of freedom error.
The Analysis of Variance Summary Table shown below is a convenient way to summarize the partitioning of the variance. The rounding errors have been corrected.
| Source | df | SSQ | MS | F | p |
|---|---|---|---|---|---|
| Condition | 3 | 27.5349 | 9.1783 | 3.465 | 0.0182 |
| Error | 132 | 349.6544 | 2.6489 | ||
| Total | 135 | 377.1893 |
The first column shows the sources of variation, the second column shows the degrees of freedom, the third shows the sums of squares, the fourth shows the mean squares, the fifth shows the \(F\) ratio, and the last shows the probability value. Note that the mean squares are always the sums of squares divided by degrees of freedom. The \(F\) and \(p\) are relevant only to Condition. Although the mean square total could be computed by dividing the sum of squares by the degrees of freedom, it is generally not of much interest and is omitted here.
Formatting Data for Computer Analysis
Most computer programs that compute ANOVAs require your data to be in a specific form. Consider the data in Table \(\PageIndex{3}\).
| Group 1 | Group 2 | Group 3 |
|---|---|---|
| 3 | 2 | 8 |
| 4 | 4 | 5 |
| 5 | 6 | 5 |
Here there are three groups, each with three observations. To format these data for a computer program, you normally have to use two variables: the first specifies the group the subject is in and the second is the score itself. The reformatted version of the data in Table \(\PageIndex{3}\) is shown in Table \(\PageIndex{4}\).
| G | Y |
|---|---|
| 1 | 3 |
| 1 | 4 |
| 1 | 5 |
| 2 | 2 |
| 2 | 4 |
| 2 | 6 |
| 3 | 8 |
| 3 | 5 |
| 3 | 5 |
To use Analysis Lab to do the calculations, you would copy the data and then
- Click the "Enter/Edit Data" button. (You may be warned that for security reasons you must use the keyboard shortcut for pasting data.)
- Paste your data.
- Click "Accept Data."
- Set the Dependent Variable to \(Y\).
- Set the Grouping Variable to \(G\).
- Click the ANOVA button.
You will find that \(F = 1.5\) and \(p = 0.296\).


