10.4: The Least Squares Regression Line
- Page ID
- 545
- To learn how to measure how well a straight line fits a collection of data.
- To learn how to construct the least squares regression line, the straight line that best fits a collection of data.
- To learn the meaning of the slope of the least squares regression line.
- To learn how to use the least squares regression line to estimate the response variable \(y\) in terms of the predictor variable \(x\).
Goodness of Fit of a Straight Line to Data
Once the scatter diagram of the data has been drawn and the model assumptions described in the previous sections at least visually verified (and perhaps the correlation coefficient \(r\) computed to quantitatively verify the linear trend), the next step in the analysis is to find the straight line that best fits the data. We will explain how to measure how well a straight line fits a collection of points by examining how well the line \(y=\frac{1}{2}x-1\) fits the data set
\[\begin{array}{c|c c c c c} x & 2 & 2 & 6 & 8 & 10 \\ \hline y &0 &1 &2 &3 &3\\ \end{array} \nonumber \]
(which will be used as a running example for the next three sections). We will write the equation of this line as \(\hat{y}=\frac{1}{2}x-1\) with an accent on the \(y\) to indicate that the \(y\)-values computed using this equation are not from the data. We will do this with all lines approximating data sets. The line \(\hat{y}=\frac{1}{2}x-1\) was selected as one that seems to fit the data reasonably well.
The idea for measuring the goodness of fit of a straight line to data is illustrated in Figure \(\PageIndex{1}\), in which the graph of the line \(\hat{y}=\frac{1}{2}x-1\) has been superimposed on the scatter plot for the sample data set.
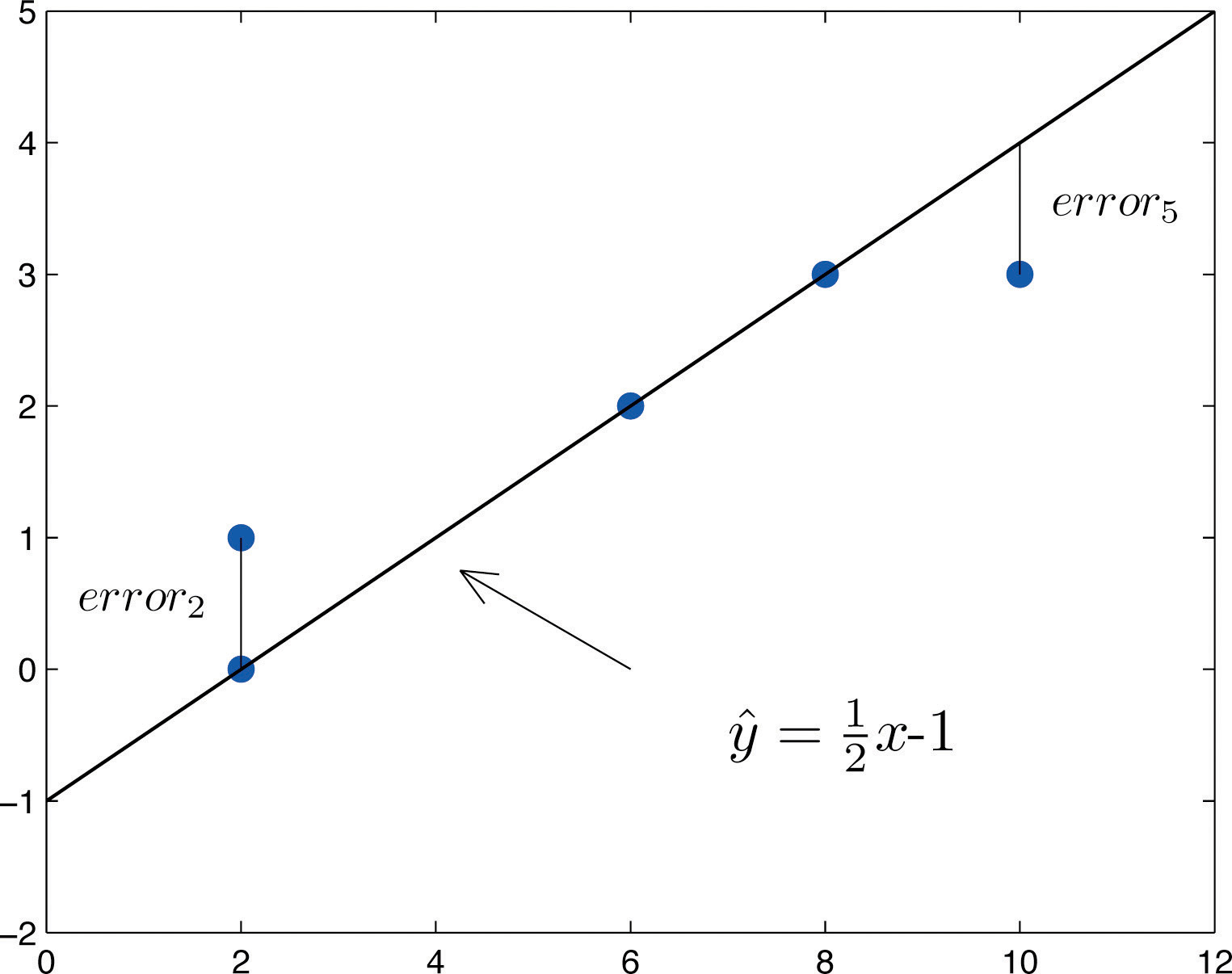
To each point in the data set there is associated an “error,” the positive or negative vertical distance from the point to the line: positive if the point is above the line and negative if it is below the line. The error can be computed as the actual \(y\)-value of the point minus the \(y\)-value \(\hat{y}\) that is “predicted” by inserting the \(x\)-value of the data point into the formula for the line:
\[\text{error at data point(x,y)}=(\text{true y})−(\text{predicted y})=y−\hat{y} \nonumber \]
The computation of the error for each of the five points in the data set is shown in Table \(\PageIndex{1}\).
| \(x\) | \(y\) | \(\hat{y}=\frac{1}{2}x-1\) | \(y-\hat{y}\) | \((y-\hat{y})^2\) | |
|---|---|---|---|---|---|
| 2 | 0 | 0 | 0 | 0 | |
| 2 | 1 | 0 | 1 | 1 | |
| 6 | 2 | 2 | 0 | 0 | |
| 8 | 3 | 3 | 0 | 0 | |
| 10 | 3 | 4 | −1 | 1 | |
| \(\sum\) | - | - | - | 0 | 2 |
A first thought for a measure of the goodness of fit of the line to the data would be simply to add the errors at every point, but the example shows that this cannot work well in general. The line does not fit the data perfectly (no line can), yet because of cancellation of positive and negative errors the sum of the errors (the fourth column of numbers) is zero. Instead goodness of fit is measured by the sum of the squares of the errors. Squaring eliminates the minus signs, so no cancellation can occur. For the data and line in Figure \(\PageIndex{1}\) the sum of the squared errors (the last column of numbers) is \(2\). This number measures the goodness of fit of the line to the data.
The goodness of fit of a line \(\hat{y}=mx+b\) to a set of \(n\) pairs \((x,y)\) of numbers in a sample is the sum of the squared errors
\[\sum (y−\hat{y})^2 \nonumber \]
(\(n\) terms in the sum, one for each data pair).
The Least Squares Regression Line
Given any collection of pairs of numbers (except when all the \(x\)-values are the same) and the corresponding scatter diagram, there always exists exactly one straight line that fits the data better than any other, in the sense of minimizing the sum of the squared errors. It is called the least squares regression line. Moreover there are formulas for its slope and \(y\)-intercept.
Given a collection of pairs \((x,y)\) of numbers (in which not all the \(x\)-values are the same), there is a line \(\hat{y}=\hat{β}_1x+\hat{β}_0\) that best fits the data in the sense of minimizing the sum of the squared errors. It is called the least squares regression line. Its slope \(\hat{β}_1\) and \(y\)-intercept \(\hat{β}_0\) are computed using the formulas
\[\hat{β}_1=\dfrac{SS_{xy}}{SS_{xx}} \nonumber \]
and
\[\hat{β}_0=\overline{y} - \hat{β}_1 x \nonumber \]
where
\[SS_{xx}=\sum x^2-\frac{1}{n}\left ( \sum x \right )^2 \nonumber \]
and
\[ SS_{xy}=\sum xy-\frac{1}{n}\left ( \sum x \right )\left ( \sum y \right ) \nonumber \]
\(\bar{x}\) is the mean of all the \(x\)-values, \(\bar{y}\) is the mean of all the \(y\)-values, and \(n\) is the number of pairs in the data set.
The equation
\[\hat{y}=\hat{β}_1x+\hat{β}_0 \nonumber \]
specifying the least squares regression line is called the least squares regression equation.
Remember from Section 10.3 that the line with the equation \(y=\beta _1x+\beta _0\) is called the population regression line. The numbers \(\hat{\beta _1}\) and \(\hat{\beta _0}\) are statistics that estimate the population parameters \(\beta _1\) and \(\beta _0\).
We will compute the least squares regression line for the five-point data set, then for a more practical example that will be another running example for the introduction of new concepts in this and the next three sections.
Find the least squares regression line for the five-point data set
\[\begin{array}{c|c c c c c} x & 2 & 2 & 6 & 8 & 10 \\ \hline y &0 &1 &2 &3 &3\\ \end{array} \nonumber \]
and verify that it fits the data better than the line \(\hat{y}=\frac{1}{2}x-1\) considered in Section 10.4.1 above.
Solution
In actual practice computation of the regression line is done using a statistical computation package. In order to clarify the meaning of the formulas we display the computations in tabular form.
| \(x\) | \(y\) | \(x^2\) | \(xy\) | |
|---|---|---|---|---|
| 2 | 0 | 4 | 0 | |
| 2 | 1 | 4 | 2 | |
| 6 | 2 | 36 | 12 | |
| 8 | 3 | 64 | 24 | |
| 10 | 3 | 100 | 30 | |
| \(\sum\) | 28 | 9 | 208 | 68 |
In the last line of the table we have the sum of the numbers in each column. Using them we compute:
\[SS_{xx}=\sum x^2-\frac{1}{n}\left ( \sum x \right )^2=208-\frac{1}{5}(28)^2=51.2 \nonumber \]
\[SS_{xy}=\sum xy-\frac{1}{n}\left ( \sum x \right )\left ( \sum y \right )=68-\frac{1}{5}(28)(9)=17.6 \nonumber \]
\[\bar{x}=\frac{\sum x}{n}=\frac{28}{5}=5.6\\ \bar{y}=\frac{\sum y}{n}=\frac{9}{5}=1.8 \nonumber \]
so that
\[\hat{β}_1=\dfrac{SS_{xy}}{SS_{xx}}=\dfrac{17.6}{51.2}=0.34375 \nonumber \]
and
\[\hat{β}_0=\bar{y}−\hat{β}_1x−=1.8−(0.34375)(5.6)=−0.125 \nonumber \]
The least squares regression line for these data is
\[\hat{y}=0.34375 x−0.125 \nonumber \]
The computations for measuring how well it fits the sample data are given in Table \(\PageIndex{2}\). The sum of the squared errors is the sum of the numbers in the last column, which is \(0.75\). It is less than \(2\), the sum of the squared errors for the fit of the line \(\hat{y}=\frac{1}{2}x-1\) to this data set.
| \(x\) | \(y\) | \(\hat{y}=0.34375x-0.125\) | \(y-\hat{y}\) | \((y-\hat{y})^2\) |
|---|---|---|---|---|
| 2 | 0 | 0.5625 | −0.5625 | 0.31640625 |
| 2 | 1 | 0.5625 | 0.4375 | 0.19140625 |
| 6 | 2 | 1.9375 | 0.0625 | 0.00390625 |
| 8 | 3 | 2.6250 | 0.3750 | 0.14062500 |
| 10 | 3 | 3.3125 | −0.3125 | 0.09765625 |
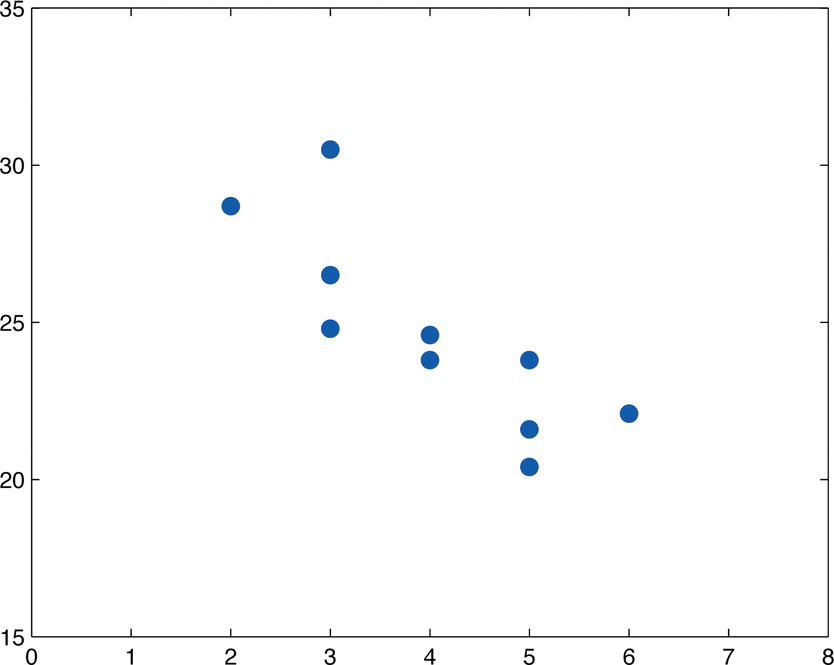
Table \(\PageIndex{3}\) shows the age in years and the retail value in thousands of dollars of a random sample of ten automobiles of the same make and model.
- Construct the scatter diagram.
- Compute the linear correlation coefficient \(r\). Interpret its value in the context of the problem.
- Compute the least squares regression line. Plot it on the scatter diagram.
- Interpret the meaning of the slope of the least squares regression line in the context of the problem.
- Suppose a four-year-old automobile of this make and model is selected at random. Use the regression equation to predict its retail value.
- Suppose a \(20\)-year-old automobile of this make and model is selected at random. Use the regression equation to predict its retail value. Interpret the result.
- Comment on the validity of using the regression equation to predict the price of a brand new automobile of this make and model.
| \(x\) | 2 | 3 | 3 | 3 | 4 | 4 | 5 | 5 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(y\) | 28.7 | 24.8 | 26.0 | 30.5 | 23.8 | 24.6 | 23.8 | 20.4 | 21.6 | 22.1 |
Solution
- The scatter diagram is shown in Figure \(\PageIndex{2}\).
- We must first compute \(SS_{xx},\; SS_{xy},\; SS_{yy}\), which means computing \(\sum x,\; \sum y,\; \sum x^2,\; \sum y^2\; \text{and}\; \sum xy\). Using a computing device we obtain \[\sum x=40\; \; \sum y=246.3\; \; \sum x^2=174\; \; \sum y^2=6154.15\; \; \sum xy=956.5 \nonumber \] Thus \[SS_{xx}=\sum x^2-\frac{1}{n}\left ( \sum x \right )^2=174-\frac{1}{10}(40)^2=14\\ SS_{xy}=\sum xy-\frac{1}{n}\left ( \sum x \right )\left ( \sum y \right )=956.5-\frac{1}{10}(40)(246.3)=-28.7\\ SS_{yy}=\sum y^2-\frac{1}{n}\left ( \sum y \right )^2=6154.15-\frac{1}{10}(246.3)^2=87.781 \nonumber \] so that \[r=\frac{SS_{xy}}{\sqrt{SS_{xx}\cdot SS_{yy}}}=\frac{-28.7}{\sqrt{(14)(87.781)}}=-0.819 \nonumber \] The age and value of this make and model automobile are moderately strongly negatively correlated. As the age increases, the value of the automobile tends to decrease.
- Using the values of \(\sum x\) and \(\sum y\) computed in part (b), \[\bar{x}=\frac{\sum x}{n}=\frac{40}{10}=4\\ \bar{y}=\frac{\sum y}{n}=\frac{246.3}{10}=24.63 \nonumber \] Thus using the values of \(SS_{xx}\) and \(SS_{xy}\) from part (b), \[\hat{\beta _1}=\frac{SS_{xy}}{SS_{xx}}=\frac{-28.7}{14}=-2.05 \nonumber \] and \[\hat{\beta _0}=\bar{y}-\hat{\beta _1}x=24.63-(-2.05)(4)=32.83 \nonumber \] The equation \(\bar{y}=\hat{\beta _1}x+\hat{\beta _0}\) of the least squares regression line for these sample data is \[\hat{y}=−2.05x+32.83 \nonumber \]
Figure \(\PageIndex{3}\) shows the scatter diagram with the graph of the least squares regression line superimposed.
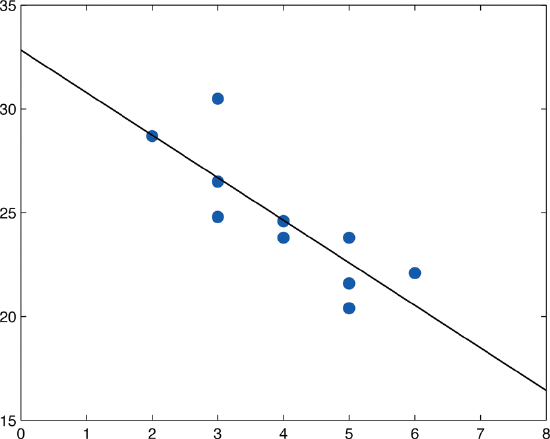
- The slope \(-2.05\) means that for each unit increase in \(x\) (additional year of age) the average value of this make and model vehicle decreases by about \(2.05\) units (about \(\$2,050\)).
- Since we know nothing about the automobile other than its age, we assume that it is of about average value and use the average value of all four-year-old vehicles of this make and model as our estimate. The average value is simply the value of \(\hat{y}\) obtained when the number \(4\) is inserted for \(x\) in the least squares regression equation: \[\hat{y}=−2.05(4)+32.83=24.63 \nonumber \] which corresponds to \(\$24,630\).
- Now we insert \(x=20\) into the least squares regression equation, to obtain \[\hat{y}=−2.05(20)+32.83=−8.17 \nonumber \] which corresponds to \(-\$8,170\). Something is wrong here, since a negative makes no sense. The error arose from applying the regression equation to a value of \(x\) not in the range of \(x\)-values in the original data, from two to six years. Applying the regression equation \(\bar{y}=\hat{\beta _1}x+\hat{\beta _0}\) to a value of \(x\) outside the range of \(x\)-values in the data set is called extrapolation. It is an invalid use of the regression equation and should be avoided.
- The price of a brand new vehicle of this make and model is the value of the automobile at age \(0\). If the value \(x=0\) is inserted into the regression equation the result is always \(\hat{\beta _0}\), the \(y\)-intercept, in this case \(32.83\), which corresponds to \(\$32,830\). But this is a case of extrapolation, just as part (f) was, hence this result is invalid, although not obviously so. In the context of the problem, since automobiles tend to lose value much more quickly immediately after they are purchased than they do after they are several years old, the number \(\$32,830\) is probably an underestimate of the price of a new automobile of this make and model.
For emphasis we highlight the points raised by parts (f) and (g) of the example.
The process of using the least squares regression equation to estimate the value of \(y\) at a value of \(x\) that does not lie in the range of the \(x\)-values in the data set that was used to form the regression line is called extrapolation. It is an invalid use of the regression equation that can lead to errors, hence should be avoided.
The Sum of the Squared Errors SSE
In general, in order to measure the goodness of fit of a line to a set of data, we must compute the predicted \(y\)-value \(\hat{y}\) at every point in the data set, compute each error, square it, and then add up all the squares. In the case of the least squares regression line, however, the line that best fits the data, the sum of the squared errors can be computed directly from the data using the following formula
The sum of the squared errors for the least squares regression line is denoted by \(SSE\). It can be computed using the formula
\[SSE=SS_{yy}−\hat{β}_1SS_{xy} \nonumber \]
Find the sum of the squared errors \(SSE\) for the least squares regression line for the five-point data set
\[\begin{array}{c|c c c c c} x & 2 & 2 & 6 & 8 & 10 \\ \hline y &0 &1 &2 &3 &3\\ \end{array} \nonumber \]
Do so in two ways:
- using the definition \(\sum (y-\hat{y})^2\);
- using the formula \(SSE=SS_{yy}-\hat{\beta }_1SS_{xy}\).
Solution
- The least squares regression line was computed in "Example \(\PageIndex{2}\)" and is \(\hat{y}=0.34375x-0.125\). SSE was found at the end of that example using the definition \(\sum (y-\hat{y})^2\). The computations were tabulated in Table \(\PageIndex{2}\). SSE is the sum of the numbers in the last column, which is \(0.75\).
- The numbers \(SS_{xy}\) and \(\hat{\beta _1}\) were already computed in "Example \(\PageIndex{2}\)" in the process of finding the least squares regression line. So was the number \(\sum y=9\). We must compute \(SS_{yy}\). To do so it is necessary to first compute \[\sum y^2=0+1^2+2^2+3^2+3^2=23 \nonumber \] Then \[SS_{yy}=\sum y^2-\frac{1}{n}\left ( \sum y \right )^2=23-\frac{1}{5}(9)^2=6.8 \nonumber \] so that \[SSE=SS_{yy}-\hat{\beta _1}SS_{xy}=6.8-(0.34375)(17.6)=0.75 \nonumber \]
Find the sum of the squared errors \(SSE\) for the least squares regression line for the data set, presented in Table \(\PageIndex{3}\), on age and values of used vehicles in "Example \(\PageIndex{3}\)".
Solution
From "Example \(\PageIndex{3}\)" we already know that
\[SS_{xy}=-28.7,\; \hat{\beta _1}=-2.05,\; \text{and}\; \sum y=246.3 \nonumber \]
To compute \(SS_{yy}\) we first compute
\[\sum y^2=28.7^2+24.8^2+26.0^2+30.5^2+23.8^2+24.6^2+23.8^2+20.4^2+21.6^2+22.1^2=6154.15 \nonumber \]
Then
\[SS_{yy}=\sum y^2-\frac{1}{n}\left ( \sum y \right )^2=6154.15-\frac{1}{10}(246.3)^2=87.781 \nonumber \]
Therefore
\[SSE=SS_{yy}-\hat{\beta _1}SS_{xy}=87.781-(-2.05)(-28.7)=28.946 \nonumber \]
- How well a straight line fits a data set is measured by the sum of the squared errors.
- The least squares regression line is the line that best fits the data. Its slope and \(y\)-intercept are computed from the data using formulas.
- The slope \(\hat{\beta _1}\) of the least squares regression line estimates the size and direction of the mean change in the dependent variable \(y\) when the independent variable \(x\) is increased by one unit.
- The sum of the squared errors \(SSE\) of the least squares regression line can be computed using a formula, without having to compute all the individual errors.


