2.6: Graphing Quantitative Variables
- Page ID
- 17303
Review Ch. 1 to refresh yourself on what quantitative variables and the ratio and interval scale of measurement describes.
Briefly, quantitative variables are variables measured on a numeric scale. Height, weight, response time, subjective rating of pain, temperature, and score on an exam are all examples of quantitative variables. Quantitative variables are distinguished from qualitative (sometimes called nominal or categorical) variables such as favorite color, religion, city of birth, favorite sport in which there is no ordering or measuring involved.
There are many types of graphs that can be used to portray distributions of quantitative variables. The upcoming sections cover the following types of graphs:
- Line graphs (sometimes called frequency polygons)
- Histograms
- Box plots
- Scatter plots
Each type of chart highlights different kinds of information. It is up to you to decide which fits your purposes best!
The Shape of Distribution
The next section will go more in-depth, and the following chapter will go into even more detail, but here is an introduction to describing the shape of graphs of quantitative variables.
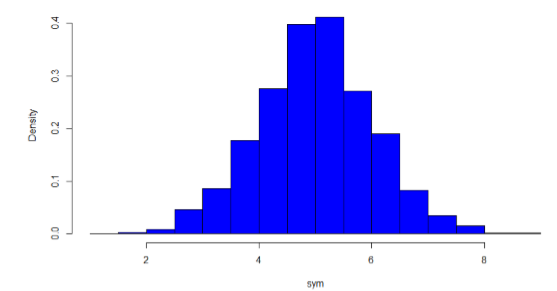
The primary characteristic we are concerned about when assessing the shape of a distribution is whether the distribution is symmetrical or skewed. A symmetrical distribution, as the name suggests, can be cut down the center to form two mirror images. Although in practice we will never get a perfectly symmetrical distribution, we would like our data to be as close to symmetrical as possible. Many types of distributions are symmetrical, but by far the most common and pertinent distribution at this point is the normal distribution, shown in Figure \(\PageIndex{1}\). Notice that although the symmetry is not perfect (for instance, the bar just to the right of the center is taller than the one just to the left), the two sides are roughly the same shape. The normal distribution has a single peak, known as the center, and two tails that extend out equally, forming what is known as a bell shape or bell curve.
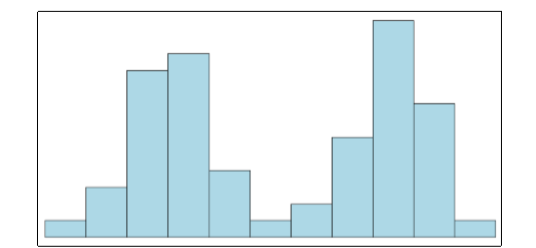
Symmetrical distributions can also have multiple peaks. Figure \(\PageIndex{2}\) shows a bimodal distribution (bimodal means two modes), named for the two peaks that lie roughly symmetrically on either side of the center point. This is relatively difficult characteristic to detect numerically. Thus, it is important to visualize your data before moving ahead with any statistical analyses.
Distributions that are not symmetrical also come in many forms, more than can be described here. The most common asymmetry to be encountered is referred to as skew, in which one of the two tails of the distribution is disproportionately longer than the other. This property can affect the value of the averages we use in our analyses and make them an inaccurate representation of our data, which causes many problems.
Skew can either be positive or negative (also known as right or left, respectively), based on which tail is longer. It is very easy to get the two confused at first; many students want to describe the skew by where the bulk of the data (larger portion of the histogram, known as the body) is placed, but the correct determination is based on which tail is longer. You can think of the tail as an arrow: whichever direction the arrow is pointing is the direction of the skew. Figures \(\PageIndex{3}\) and \(\PageIndex{4}\) show positive (right) and negative (left) skew, respectively.
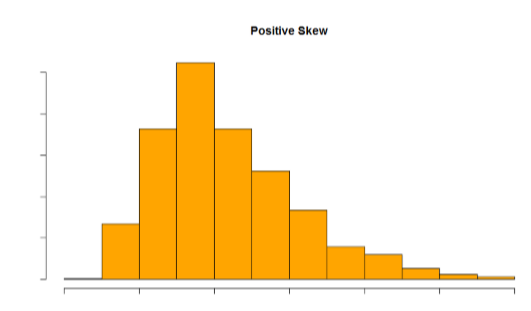
Figure \(\PageIndex{3}\): A positively skewed distribution in a histogram (CC-BY-NC-SA Foster et al. from An Introduction to Psychological Statistics)
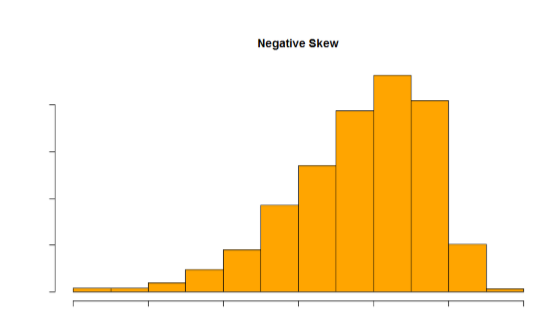
The next section will go into more detail about skew, and introduce you to a new term to describe different shapes of symmetrical distributions.
Contributors and Attributions
-
Foster et al. (University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus)


