12.1: Introduction to Repeated Measures ANOVA
- Page ID
- 22121
This chapter will introduce a new kind of ANOVA, so we'll know about two kinds of ANOVAs:
- Between-Groups ANOVA: We collect the quantitative variable from each participant, who is only in one condition of the qualitative variable.
This is what we’ve been doing.
Is this more like an independent t-test or a dependent t-test?
Solution
This is more like an independent t-test because the participants in the separate groups are unrelated to each other.
- Within-Groups ANOVA: We collect the quantitative variable from each participant, who is in all conditions of the qualitative variable.
Is this more like an independent t-test or a dependent t-test?
- Answer
-
This is more like a dependent t-test because the participants are in all ofthe conditions, or are somehow linked with participants in each of the different groups (levels of the IV).
RM ANOVAs are still ANOVAs, we’re still looking at the ratio of between groups variability to within groups variability. With repeated measures, we just have more information. Our total variation is comprised of:
- Within group variation which we can’t measure directly,
- Individual differences, which we can measure indirectly, and
- Between group differences, which we can measure directly.
Comparison of BG & WG ANOVA
- Data collection is different for the two
- BG - each participant is only in one condition/group
- RM- each participant will be in all conditions/groups
- SAME hypotheses:
- Research hypothesis: Mean difference in a specific direction
- Null hypothesis: No mean differences between the groups
- Formulas and computation is different for BG & WG
- Both use an ANOVA Summary Table, but RM has an extra row for the within-participant source of variation
Partitioning Variation
Time to introduce a new name for an idea you learned about last chapter, it’s called partitioning the sums of squares. Sometimes an obscure new name can be helpful for your understanding of what is going on. ANOVAs are all about partitioning the sums of squares. We already did some partitioning in the last chapter. What do we mean by partitioning?
The act of partitioning, or splitting up, is the core idea of ANOVA. To use the house analogy. We want to split our total sums of squares (SS Total) up into littler pieces. Before we partitioned SS Total using this formula:
\[SS_\text{TOTAL} = SS_\text{BG Effect} + SS_\text{WG Error} \nonumber \]
Remember, the \(SS_\text{BG Effect}\) was the variance we could attribute to the means of the different groups, and \(SS_\text{wG Error}\) was the leftover variance that we couldn’t explain. \(SS_\text{BG Effect}\) and \(SS_\text{WG Error}\) are the partitions of \(SS_\text{TOTAL}\), they are the littler pieces that combine to make the whole.
In the Between Groups ANOVA, we got to split \(SS_\text{TOTAL}\) into two parts. What is most interesting about the Repeated Measures ANOVA (sometimes known as Within-Groups ANOVA), is that we get to split \(SS_\text{TOTAL}\) into three parts, there’s one more little piece. Can you guess what the new partition is? Here is the new idea for partitioning \(SS_\text{TOTAL}\) in a Repeated Measures ANOVA:
\[SS_\text{TOTAL} = SS_\text{BG Effect} + SS_\text{Participants} + SS_\text{WG Error} \nonumber \]
We’ve added \(SS_\text{Participants}\) as the new idea in the formula. What’s the idea here? Well, because each participant was measured in each condition (more than once), we have a new set of means. These are the means for each participant, collapsed across the conditions. For example, if we had a study in which each participant was measured three time (Before, During, After), then Participant 1 has a mean (an average of their three scores); Participant 2 has a mean (an average of their three scores); and so on. We can now estimate the portion of the total variance that is explained by the means of these participants.
We just showed you a conceptual “formula” to split up \(SS_\text{TOTAL}\) into three parts. All of these things have different names, though. To clarify, we will confuse you just a little bit. Be prepared to be confused a little bit.
A Rose by Any Other Name
First, the Repeated Measures ANOVA has different names. Sometimes it's called a Within-Groups ANOVA, and you could even call it an ANOVA with Dependent Groups (although I've never actually seen anyone do that). The point is, these are all the same analysis. "Repeated Measures" means that each participant is measured in each condition, like in our Before, During, and After example above. This is pretty clear, and that's why I call this ANOVA the RM ANOVA. However, sometimes it's not the same person in each condition, but three people who are related, or dependent upon each other. For example, let's say that we did a study comparing families with three kids to see if birth order matters. Each family has three different kids, but the kids are definitely related and dependent on each other. We would need an analysis that takes into account that inter-relatedness. I mean, we could use a Between Groups ANOVA, but that information about how the three kids are treated similarly or affect each other would become noise in a BG ANOVA and mask differences based on birth order.
You might notice that this is a design issue (how data is collected), not an analysis issue. That's why it doesn't really matter what it's called, as long as we all agree on how to analyze this related data. If you're a psychology or sociology major, you'll probably take a class called Research Methods which will talk about these design issues in detail.
Second, different statisticians use different words to describe parts of the ANOVA. This can be really confusing. For example, we described the SS formula for a between subjects design like this:
\[SS_\text{TOTAL} = SS_\text{BG Effect} + SS_\text{Participants} + SS_\text{WG Error} \nonumber \]
To have something called "between groups" in the formula might make you think that you're conducting a Between Groups ANOVA, when it's really just describing the partition comparing the different groups. We think this is very confusing for people. Here "within groups" has a special meaning. It does not refer to a within-groups or repeated measures design. \(SS_\text{WG Error}\) refers to the leftover variation within each group mean. Specifically, it is the variation between each group mean and each score in the group. “AAGGH, you’ve just used the word between to describe within group variation!”. Yes! We feel your pain. Remember, for each group mean, every score is probably off a little bit from the mean. So, the scores within each group have some variation. This is the within group variation, and it is why the leftover error that we can’t explain is often called \(SS_\text{WG Error}\). It is error caused by the variation within each group.
We’re getting there, but perhaps a picture will help to clear things up. Note that Figure \(\PageIndex{1}\) uses the outdated name for the within-participant variation as "Subjects".
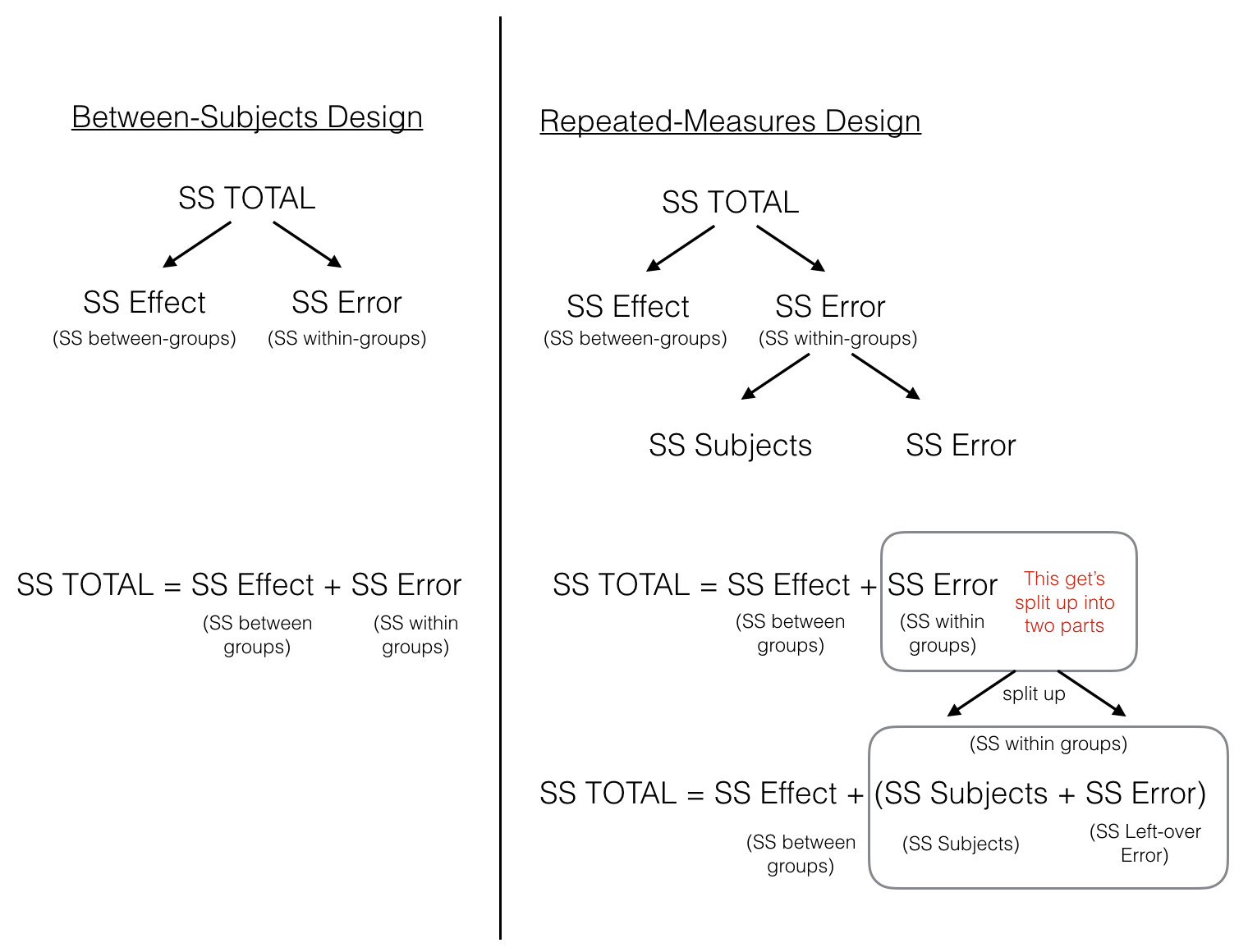
The figure lines up the partitioning of the Sums of Squares for both Between Groups ANOVA and Repeated Measures ANOVA designs. In both designs, \(SS_\text{Total}\) is first split up into two pieces \(SS_\text{Effect (between-groups)}\) and \(SS_\text{Error (within-groups)}\). At this point, both ANOVAs are the same. In the repeated measures case we split the \(SS_\text{Error (within-groups)}\) into two more littler parts, which we call \(SS_\text{Subjects (error variation about the subject mean)}\) and \(SS_\text{Error (left-over variation we can't explain)}\).
So, when we earlier wrote the formula to split up SS in the repeated-measures design, we were kind of careless in defining what we actually meant by \(SS_\text{Error}\), this was a little too vague:
\[SS_\text{TOTAL} = SS_\text{BG Effect} + SS_\text{Partipants} +SS_\text{WG Error} \nonumber \]
The critical feature of the Repeated Measures ANOVA, is that the \(SS_\text{WG Error}\) that we will later use to compute the Mean Square in the denominator for the \(F\)-value, is smaller in a repeated measures design, compared to a between subjects design. This is because the \(SS_\text{Error (within-groups)}\) is split into two parts, \(SS_\text{Subjects (error variation about the subject mean)}\) and \(SS_\text{Error (left-over variation we can't explain)}\).
To make this more clear, Dr. Crump made another Figure \(\PageIndex{2}\):
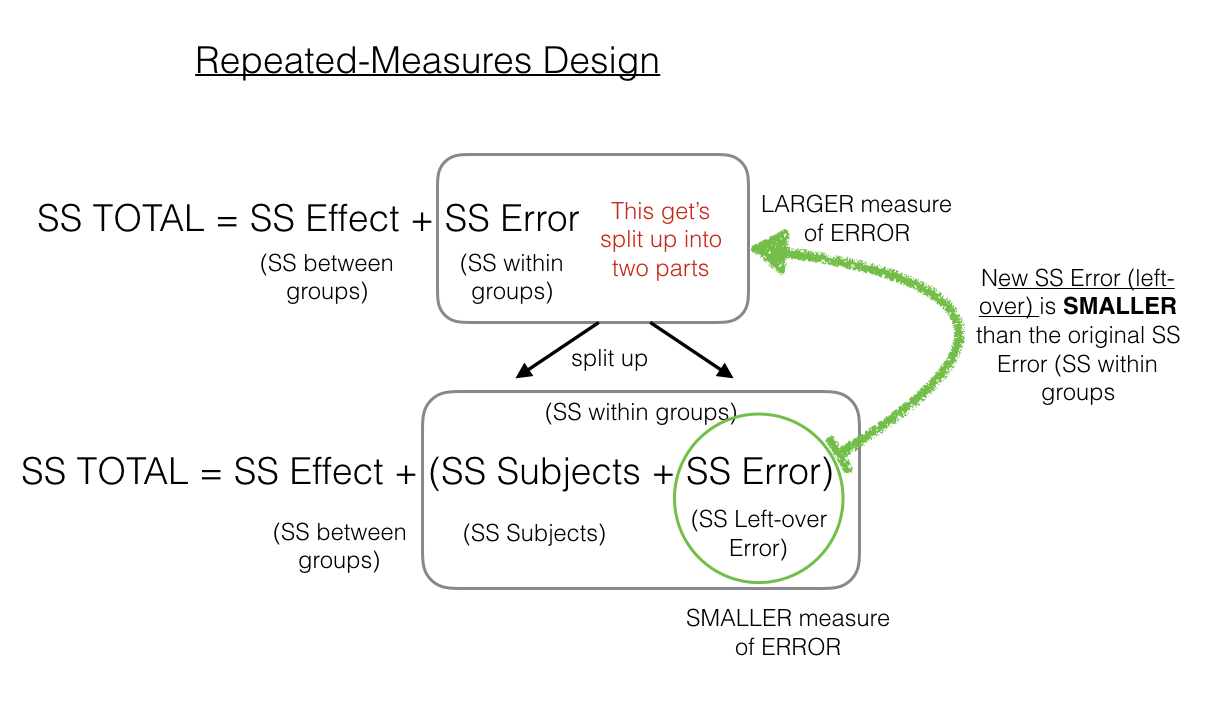
As we point out, the \(SS_\text{Error (left-over)}\) in the green circle will be a smaller number than the \(SS_\text{Error (within-group)}\). That’s because we are able to subtract out the \(SS_\text{Subjects}\) part of the \(SS_\text{Error (within-group)}\). As we will see shortly, this can have the effect of producing larger F-values when using a repeated-measures design compared to a between-subjects design.
What does this new kind of variation look like in the ANOVA Summary Table? Let's look!


