8.3: One-Sample t-test Calculations
- Page ID
- 22080
Statistical analyses can be confusing. To make it easier, Dr. Foster and his colleagues use these four steps. For a thorough analysis, these steps should be completed after you review the descriptive statistics (measures of central tendencies of mean, median, and mode; standard deviation as a measure of variability) and the data graphed in a frequency chart.
- Stating the Hypothesis
- Finding the Critical Values
- Computing the Test Statistic
- Making the Decision.
Practice Example
We will work though an example.
Scenario:
Imagine that you hear that most students spend about 30 minutes studying for their weekly quizzes. You ask four students who sit next to you in your behavioral statistics course how long they study for their weekly quizzes.
Step 1: State the Hypotheses
We still state the research hypothesis and the null hypotheses mathematically in terms of the population parameter and written out in readable English. For our example:
- Research Hypothesis: The students who sit next to me in my behavioral statistics course study for longer than the the population of students studies for their quizzes.
- Note that this has all of the required components of a complete research hypothesis discussed in 7.3: The Research Hypothesis and Null Hypotheses:
- The name of the groups being compared: The four people sitting next to you in your behavioral statistics class, compared to all students.
- What was measured: Time spend studying
- Which group are we predicting will have the higher mean: The sample of four people will be higher ("study for longer").
- Symbols: \( \bar{X} > μ \)
- Note that this has all of the required components of a complete research hypothesis discussed in 7.3: The Research Hypothesis and Null Hypotheses:
- Null Hypothesis: The students who sit next to me in my behavioral statistics course study for about the same amount of time as the population of students study for their quizzes.
- Symbols: \( \bar{X} = μ \)
Step 2: Find the Critical Values
Critical values still delineate the area in the tails under the curve corresponding to our chosen level of significance. Because we have no reason to change significance levels, we will use \(α\) = 0.05, and because we suspect a direction of effect, we have a one-tailed test. To find our critical values for \(t\), we need to add one more piece of information: the degrees of freedom. In almost all cases, degrees of freedom (or df) are N-1. So, for this example:
\[df = N – 1 = 4 – 1 = 3 \nonumber \]
You can find the table of critical t-scores page, or go to the Common Critical Values page at the end of the book (in Back Matter) to find a link to all of the critical value tables that we'll be using.
Going to our table of critical t-scores page, we find the the number 4 in the Degrees of Freedom column (all the way on the left), then follow that to the p = .05 column (middle column). Doing that, our critical value is \(t\) = 2.353. You can use Figure \(\PageIndex{1}\) to visualize our rejection region.
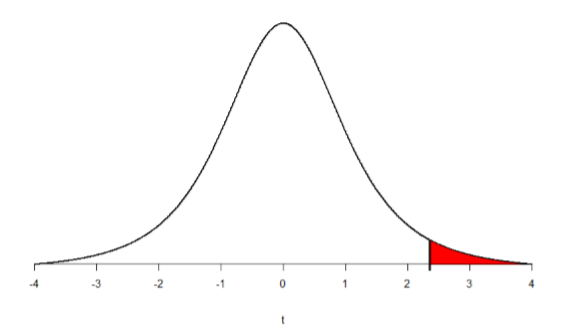
Step 3: Compute the Test Statistic
The answers to how long they study for the weekly quiz last week from your four classmates are below in Table \(\PageIndex{1}\). You can use these to calculate \(\overline{\mathrm{X}}\) and s by filling in the rest of the Table \(\PageIndex{1}\). These are worked out in the Exercise \(\PageIndex{1}\).
| \(\overline{\mathrm{X}}\) | \(\mathrm{X}-\overline{\mathrm{X}}\) | \((\mathrm{X}-\overline{\mathrm{X}})^{2}\) |
|---|---|---|
| 46 | ||
| 58 | ||
| 40 | ||
| 71 | ||
| \(\Sigma\)=215 | \(\Sigma\)=0 | \(\Sigma\)= ??? |
Use the four data points in the table to determine the mean and standard deviation of the sample of four classmates.
- Answer
-
Table \(\PageIndex{2}\): Sum of Squares Table \(\mathrm{X}\) \(\mathrm{X}-\overline{\mathrm{X}}\) \((\mathrm{X}-\overline{\mathrm{X}})^{2}\) 46 -7.75 60.06 58 4.25 18.06 40 -13.75 189.06 71 17.25 297.56 \(\Sigma\)=215 \(\Sigma\)=0 \(\Sigma\)=564.75 Mean:
As the table shows, the sum of the time spent studying for our four classmates was 215 minutes. We can use this to find that the mean:
\[ \overline{\mathrm{X}} = \dfrac {215}{4} = 53.75 \nonumber \]
Our four classmates studied for the weekly quiz an average of 53.75 minutes.
Standard Deviation:
We use that mean to subtract each score from (middle column), then square each score (right column). Summing that last column, you should get a sum of squares of \(SS\) = 564.75/. If you are close (anywhere from 564.70 to 564.80), then your calculator or software are rounding slightly differently. Don't worry! Your answer is close enough.
We then plug in to the formula for standard deviation from chapter 3:
\[s=\sqrt{\dfrac{\sum(X-\overline{X})^{2}}{N-1}}=\sqrt{\dfrac{S S}{d f}}=\sqrt{\dfrac{564.75}{4-1}}=\sqrt{\dfrac{564.75}{3}}= \sqrt{188.25}= 13.72 \nonumber \]
Okay, now that we have the mean of the sample (\( \overline{\mathrm{X}} = 53.75 \)) and a standard deviation for the sample (\(s = 13.72 \)), and we still know N (and the Degrees of Freedom), we plug it all into the t-test formula!
\[t=\cfrac{(\bar{X}-\mu)}{\left(\cfrac{s} {\sqrt{n}}\right)} = \cfrac{(53.75 - 30)}{\left(\cfrac{13.72} {\sqrt{4}}\right)} = \cfrac{(23.75)}{\left(\cfrac{13.72} {2}\right)} = \dfrac{23.75}{6.86} = 3.46 \nonumber \]
This may seem like a lot of steps, but it is really just taking our raw data to calculate one value at a time and carrying that value forward into the next equation. At each step, we simply match the symbols of what we just calculated to where they appear in the next formula to make sure we are plugging everything in correctly.
Step 4: Make the Decision
This is a behavioral statistics course, so you're not done!
Now that we have our critical value and test statistic, we can make our decision. Our calculated \(t\)-statistic was \(t\) = 3.46 and our critical value was \(t = 2.353\). So, do we retain the null hypothesis or reject the null hypothesis? Since our calculated t-score was more extreme than our critical value, we reject the null hypothesis.
Let's add these critical and calculated values to our cheat sheet on understanding how to make the decision:
\((Critical < |Calculated|) =\) Reject null \(=\) means are different \(= p<.05\)
\((Critical > |Calculated|) =\) Retain null \(=\) means are similar \(= p>.05\)
This shows us that when the critical value from the table is smaller than the absolute value of our calcluated, then we reject the null hypothesis, say that the means are different (the higher mean is larger), and that p<0.05 (the probability that the sample mean is similar to the population mean is small).
We're still not done!
Write-Up
"Based on our sample of four classmates, the sample studied longer on average (\(\overline{\mathrm{X}}\) = 53.75 minutes) than the population of students (\( \mu \) = 30 minutes), \(t(3)\) = 3.46, \(p\) < 0.05."
Notice that we also include the degrees of freedom in parentheses after the \(t\).
Students always get confused about which way the sign goes between the "p" and the 0.05. The first thing to remember is that it's like Pac-Man, and will eat whatever is bigger. The sample mean is so much larger than the population mean that p=.05 is bigger than the probability of getting this sample mean by chance if the sample really was similar to the population.
The next section talks about this write-up part in more detail.


