4.1: Probability Density Functions (PDFs) and Cumulative Distribution Functions (CDFs) for Continuous Random Variables
- Page ID
- 3265
Probability Density Functions (PDFs)
Recall that continuous random variables have uncountably many possible values (think of intervals of real numbers). Just as for discrete random variables, we can talk about probabilities for continuous random variables using density functions.
Definition \(\PageIndex{1}\)
The probability density function (pdf), denoted \(f\), of a continuous random variable \(X\) satisfies the following:
- \(f(x) \geq 0\), for all \(x\in\mathbb{R}\)
- \(f\) is piecewise continuous
- \(\displaystyle{\int\limits^{\infty}_{-\infty}\! f(x)\,dx = 1}\)
- \(\displaystyle{P(a\leq X\leq b) = \int\limits^b_a\! f(x)\,dx}\)
The first three conditions in the definition state the properties necessary for a function to be a valid pdf for a continuous random variable. The fourth condition tells us how to use a pdf to calculate probabilities for continuous random variables, which are given by integrals the continuous analog to sums.
Example \(\PageIndex{1}\)
Let the random variable \(X\) denote the time a person waits for an elevator to arrive. Suppose the longest one would need to wait for the elevator is 2 minutes, so that the possible values of \(X\) (in minutes) are given by the interval \([0,2]\). A possible pdf for \(X\) is given by
$$f(x) = \left\{\begin{array}{l l}
x, & \text{for}\ 0\leq x\leq 1 \\
2-x, & \text{for}\ 1< x\leq 2 \\
0, & \text{otherwise}
\end{array}\right.\notag$$
The graph of \(f\) is given below, and we verify that \(f\) satisfies the first three conditions in Definition 4.1.1:
- From the graph, it is clear that \(f(x) \geq 0\), for all \(x \in \mathbb{R}\).
- Since there are no holes, jumps, asymptotes, we see that \(f(x)\) is (piecewise) continuous.
- Finally we compute:
$$\int\limits^{\infty}_{-\infty}\! f(x)\,dx = \int\limits^{2}_0\! x\,dx = \int\limits^1_0\! x\,dx + \int\limits^2_1\! (2-x)\,dx = 1\notag$$
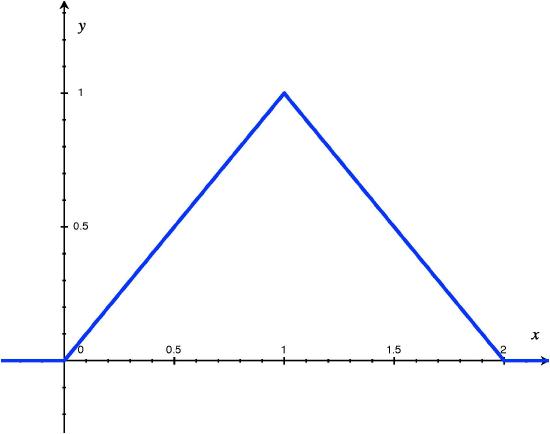
Figure 1: Graph of pdf for \(X\), \(f(x)\)
So, if we wish to calculate the probability that a person waits less than 30 seconds (or 0.5 minutes) for the elevator to arrive, then we calculate the following probability using the pdf and the fourth property in Definition 4.1.1:
$$P(0\leq X\leq 0.5) = \int\limits^{0.5}_0\! f(x)\,dx = \int\limits^{0.5}_0\! x\,dx = 0.125\notag$$
Note that, unlike discrete random variables, continuous random variables have zero point probabilities, i.e., the probability that a continuous random variable equals a single value is always given by 0. Formally, this follows from properties of integrals:
$$P(X=a) = P(a\leq X\leq a) = \int\limits^a_a\! f(x)\, dx = 0.\notag$$
Informally, if we realize that probability for a continuous random variable is given by areas under pdf's, then, since there is no area in a line, there is no probability assigned to a random variable taking on a single value. This does not mean that a continuous random variable will never equal a single value, only that we do not assign any probability to single values for the random variable. For this reason, we only talk about the probability of a continuous random variable taking a value in an INTERVAL, not at a point. And whether or not the endpoints of the interval are included does not affect the probability. In fact, the following probabilities are all equal:
$$P(a\leq X\leq b) = P(a<X<b) = P(a\leq X< b) = P(a< X \leq b) = \int\limits^b_a\!f(x)\,dx\notag$$
Cumulative Distribution Functions (CDFs)
Recall Definition 3.2.2, the definition of the cdf, which applies to both discrete and continuous random variables. For continuous random variables we can further specify how to calculate the cdf with a formula as follows. Let \(X\) have pdf \(f\), then the cdf \(F\) is given by
$$F(x) = P(X\leq x) = \int\limits^x_{-\infty}\! f(t)\, dt, \quad\text{for}\ x\in\mathbb{R}.\notag$$
In other words, the cdf for a continuous random variable is found by integrating the pdf. Note that the Fundamental Theorem of Calculus implies that the pdf of a continuous random variable can be found by differentiating the cdf. This relationship between the pdf and cdf for a continuous random variable is incredibly useful.
Relationship between PDF and CDF for a Continuous Random Variable
Let \(X\) be a continuous random variable with pdf \(f\) and cdf \(F\).
- By definition, the cdf is found by integrating the pdf:
$$F(x) = \int\limits^x_{-\infty}\! f(t)\, dt\notag$$ - By the Fundamental Theorem of Calculus, the pdf can be found by differentiating the cdf:
$$f(x) = \frac{d}{dx}\left[F(x)\right]\notag$$
Example \(\PageIndex{2}\)
Continuing in the context of Example 4.1.1, we find the corresponding cdf. First, let's find the cdf at two possible values of \(X\), \(x=0.5\) and \(x=1.5\):
\begin{align*}
F(0.5) &= \int\limits^{0.5}_{-\infty}\! f(t)\, dt = \int\limits^{0.5}_0\! t\, dt = \frac{t^2}{2}\bigg|^{0.5}_0 = 0.125 \\
F(1.5) &= \int\limits^{1.5}_{-\infty}\! f(t)\, dt = \int\limits^{1}_0\! t\, dt + \int\limits^{1.5}_1 (2-t)\, dt = \frac{t^2}{2}\bigg|^{1}_0 + \left(2t - \frac{t^2}{2}\right)\bigg|^{1.5}_1 = 0.5 + (1.875-1.5) = 0.875
\end{align*}
Now we find \(F(x)\) more generally, working over the intervals that \(f(x)\) has different formulas:
\begin{align*}
\text{for}\ x<0: \quad F(x) &= \int\limits^x_{-\infty}\! 0\, dt = 0 \\
\text{for}\ 0\leq x\leq 1: \quad F(x) &= \int\limits^{x}_{0}\! t\, dt = \frac{t^2}{2}\bigg|^x_0 = \frac{x^2}{2} \\
\text{for}\ 1<x\leq2: \quad F(x) &= \int\limits^{1}_0\! t\, dt + \int\limits^{x}_1 (2-t)\, dt = \frac{t^2}{2}\bigg|^{1}_0 + \left(2t - \frac{t^2}{2}\right)\bigg|^x_1 = 0.5 + \left(2x - \frac{x^2}{2}\right) - (2 - 0.5) = 2x - \frac{x^2}{2} - 1 \\
\text{for}\ x>2: \quad F(x) &= \int\limits^x_{-\infty}\! f(t)\, dt = 1
\end{align*}
Putting this altogether, we write \(F\) as a piecewise function and Figure 2 gives its graph:
$$F(x) = \left\{\begin{array}{l l}
0, & \text{for}\ x<0 \\
\frac{x^2}{2}, & \text{for}\ 0\leq x \leq 1 \\
2x - \frac{x^2}{2} - 1, & \text{for}\ 1< x\leq 2 \\
1, & \text{for}\ x>2
\end{array}\right.\notag$$
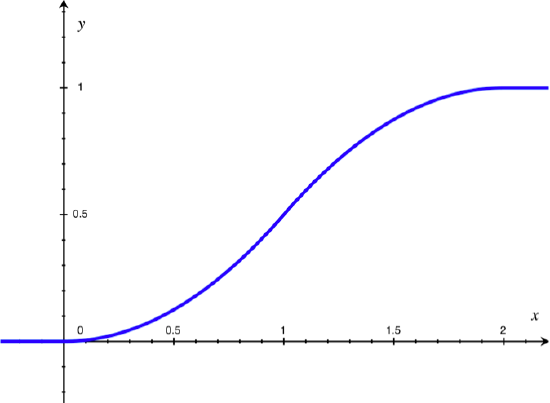
Figure 2: Graph of cdf in Example 4.1.2
Recall that the graph of the cdf for a discrete random variable is always a step function. Looking at Figure 2 above, we note that the cdf for a continuous random variable is always a continuous function.
Percentiles of a Distribution
Definition \(\PageIndex{2}\)
The (100p)th percentile (\(0\leq p\leq 1\)) of a probability distribution with cdf \(F\) is the value \(\pi_p\) such that $$F(\pi_p) = P(X\leq \pi_p) = p.\notag$$
To find the percentile \(\pi_p\) of a continuous random variable, which is a possible value of the random variable, we are specifying a cumulative probability \(p\) and solving the following equation for \(\pi_p\):
$$\int^{\pi_p}_{-\infty} f(t)dt = p\notag$$
Special Cases: There are a few values of \(p\) for which the corresponding percentile has a special name.
- Median or \(50^{th}\) percentile: \(\pi_{.5} = \mu = Q_2\), separates probability (area under pdf) into two equal halves
- 1st Quartile or \(25^{th}\) percentile: \(\pi_{.25} = Q_1\), separates \(1^{st}\) quarter (25%) of probability (area) from the rest
- 3rd Quartile or \(75^{th}\) percentile: \(\pi_{.75} = Q_3\), separates \(3^{rd}\) quarter (75%) of probability (area) from the rest
Example \(\PageIndex{3}\)
Continuing in the context of Example 4.1.2, we find the median and quartiles.
- median: find \(\pi_{.5}\), such that \(F(\pi_{.5}) = 0.5 \Rightarrow \pi_{.5} = 1\) (from graph in Figure 1)
- 1st quartile: find \(Q_1 = \pi_{.25}\), such that \(F(\pi_{.25}) = 0.25\). For this, we use the formula and the graph of the cdf in Figure 2:
$$\frac{\pi_{.25}^2}{2} = 0.25 \Rightarrow Q_1 = \pi_{.25} = \sqrt{0.5} \approx 0.707\notag$$ - 3rd quartile: find \(Q_3 = \pi_{.75}\), such that \(F(\pi_{.75}) = 0.75\). Again, use the graph of the cdf:
$$2\pi_{.75} - \frac{\pi_{.75}^2}{2} - 1 = 0.75\ \Rightarrow\ (\text{using Quadratic Formula})\ Q_3 = \pi_{.75} = \frac{4-\sqrt{2}}{2} \approx 1.293\notag$$


