13.6: Unequal Sample Sizes
- Last updated
- Save as PDF
- Page ID
- 28988
Learning Objectives
- State why unequal \(n\) can be a problem
- Define confounding
- Compute weighted and unweighted means
- Distinguish between Type I and Type III sums of squares
- Describe why the cause of the unequal sample sizes makes a difference in the interpretation
The Problem of Confounding
Whether by design, accident, or necessity, the number of subjects in each of the conditions in an experiment may not be equal. For example, the sample sizes for the "Bias Against Associates of the Obese" case study are shown in Table \(\PageIndex{1}\). Although the sample sizes were approximately equal, the "Acquaintance Typical" condition had the most subjects. Since \(n\) is used to refer to the sample size of an individual group, designs with unequal sample sizes are sometimes referred to as designs with unequal \(n\).
| Companion Weight | |||
|---|---|---|---|
| Obese | Typical | ||
| Relationship | Girlfriend | 40 | 42 |
| Acquaintance | 40 | 54 | |
We consider an absurd design to illustrate the main problem caused by unequal \(n\). Suppose an experimenter were interested in the effects of diet and exercise on cholesterol. The sample sizes are shown in Table \(\PageIndex{2}\).
| Exercise | |||
|---|---|---|---|
| Moderate | None | ||
| Diet | Low Fat | 5 | 0 |
| High Fat | 0 | 5 | |
What makes this example absurd is that there are no subjects in either the "Low-Fat No-Exercise" condition or the "High-Fat Moderate-Exercise" condition. The hypothetical data showing change in cholesterol are shown in Table \(\PageIndex{3}\).
| Exercise | ||||
|---|---|---|---|---|
| Moderate | None | Mean | ||
| Diet | Low Fat | -20 | -25 | |
| -25 | ||||
| -30 | ||||
| -35 | ||||
| -15 | ||||
| High Fat | -20 | -5 | ||
| 6 | ||||
| -10 | ||||
| -6 | ||||
| 5 | ||||
| Mean | -25 | -5 | -15 | |
The last column shows the mean change in cholesterol for the two Diet conditions, whereas the last row shows the mean change in cholesterol for the two Exercise conditions. The value of \(-15\) in the lower-right-most cell in the table is the mean of all subjects.
We see from the last column that those on the low-fat diet lowered their cholesterol an average of \(25\) units, whereas those on the high-fat diet lowered theirs by only an average of \(5\) units. However, there is no way of knowing whether the difference is due to diet or to exercise since every subject in the low-fat condition was in the moderate-exercise condition and every subject in the high-fat condition was in the no-exercise condition. Therefore, Diet and Exercise are completely confounded. The problem with unequal \(n\) is that it causes confounding.
Weighted and Unweighted Means
The difference between weighted and unweighted means is a difference critical for understanding how to deal with the confounding resulting from unequal \(n\).
Weighted and unweighted means will be explained using the data shown in Table \(\PageIndex{4}\). Here, Diet and Exercise are confounded because \(80\%\) of the subjects in the low-fat condition exercised as compared to \(20\%\) of those in the high-fat condition. However, there is not complete confounding as there was with the data in Table \(\PageIndex{3}\).
The weighted mean for "Low Fat" is computed as the mean of the "Low-Fat Moderate-Exercise" mean and the "Low-Fat No-Exercise" mean, weighted in accordance with sample size. To compute a weighted mean, you multiply each mean by its sample size and divide by \(N\), the total number of observations. Since there are four subjects in the "Low-Fat Moderate-Exercise" condition and one subject in the "Low-Fat No-Exercise" condition, the means are weighted by factors of \(4\) and \(1\) as shown below, where \(M_W\) is the weighted mean.
\[M_W=\frac{(4)(-27.5)+(1)(-20)}{5}=-26\]
The weighted mean for the low-fat condition is also the mean of all five scores in this condition. Thus if you ignore the factor "Exercise," you are implicitly computing weighted means.
The unweighted mean for the low-fat condition (\(M_U\)) is simply the mean of the two means.
\[M_U=\frac{-27.5-20}{2}=-23.75\]
| Exercise | |||||
|---|---|---|---|---|---|
| Moderate | None | Weighted Mean | Unweighted Mean | ||
| Diet | Low Fat | -20 | -20 | -26 | -23.750 |
| -25 | |||||
| -30 | |||||
| -35 | |||||
| M=-27.5 | M=-20.0 | ||||
| High Fat | -15 | 6 | -4 | -8.125 | |
| -6 | |||||
| 5 | |||||
| -10 | |||||
| M=-15.0 | M=-1.25 | ||||
| Weighted Mean | -25 | -5 | |||
| Unweighted Mean | -21.25 | -10.625 | |||
One way to evaluate the main effect of Diet is to compare the weighted mean for the low-fat diet (\(-26\)) with the weighted mean for the high-fat diet (\(-4\)). This difference of \(-22\) is called "the effect of diet ignoring exercise" and is misleading since most of the low-fat subjects exercised and most of the high-fat subjects did not. However, the difference between the unweighted means of \(-15.625\) (\((-23.750)-(-8.125)\)) is not affected by this confounding and is therefore a better measure of the main effect. In short, weighted means ignore the effects of other variables (exercise in this example) and result in confounding; unweighted means control for the effect of other variables and therefore eliminate the confounding.
Statistical analysis programs use different terms for means that are computed controlling for other effects. SPSS calls them estimated marginal means, whereas SAS and SAS JMP call them least squares means.
Types of Sums of Squares
The section on Multi-Factor ANOVA stated that when there are unequal sample sizes, the sum of squares total is not equal to the sum of the sums of squares for all the other sources of variation. This is because the confounded sums of squares are not apportioned to any source of variation. For the data in Table \(\PageIndex{4}\), the sum of squares for Diet is \(390.625\), the sum of squares for Exercise is \(180.625\), and the sum of squares confounded between these two factors is \(819.375\) (the calculation of this value is beyond the scope of this introductory text). In the ANOVA Summary Table shown in Table \(\PageIndex{5}\), this large portion of the sums of squares is not apportioned to any source of variation and represents the "missing" sums of squares. That is, if you add up the sums of squares for Diet, Exercise, \(D \times E\), and Error, you get \(902.625\). If you add the confounded sum of squares of \(819.375\) to this value, you get the total sum of squares of \(1722.000\). When confounded sums of squares are not apportioned to any source of variation, the sums of squares are called Type III sums of squares. Type III sums of squares are, by far, the most common and if sums of squares are not otherwise labeled, it can safely be assumed that they are Type III.
| Source | df | SSQ | MS | F | p |
|---|---|---|---|---|---|
| Diet | 1 | 390.625 | 390.625 | 7.42 | 0.034 |
| Exercise | 1 | 180.625 | 180.625 | 3.43 | 0.113 |
| D x E | 1 | 15.625 | 15.625 | 0.30 | 0.605 |
| Error | 6 | 315.750 | 52.625 | ||
| Total | 9 | 1722.000 |
When all confounded sums of squares are apportioned to sources of variation, the sums of squares are called Type I sums of squares. The order in which the confounded sums of squares are apportioned is determined by the order in which the effects are listed. The first effect gets any sums of squares confounded between it and any of the other effects. The second gets the sums of squares confounded between it and subsequent effects, but not confounded with the first effect, etc. The Type I sums of squares are shown in Table \(\PageIndex{6}\). As you can see, with Type I sums of squares, the sum of all sums of squares is the total sum of squares.
| Source | df | SSQ | MS | F | p |
|---|---|---|---|---|---|
| Diet | 1 | 1210.000 | 1210.000 | 22.99 | 0.003 |
| Exercise | 1 | 180.625 | 180.625 | 3.43 | 0.113 |
| D x E | 1 | 15.625 | 15.625 | 0.30 | 0.605 |
| Error | 6 | 315.750 | 52.625 | ||
| Total | 9 | 1722.000 |
In Type II sums of squares, sums of squares confounded between main effects are not apportioned to any source of variation, whereas sums of squares confounded between main effects and interactions are apportioned to the main effects. In our example, there is no confounding between the \(D \times E\) interaction and either of the main effects. Therefore, the Type II sums of squares are equal to the Type III sums of squares.
Which Type of Sums of Squares to Use (optional)
Type I sums of squares allow the variance confounded between two main effects to be apportioned to one of the main effects. Unless there is a strong argument for how the confounded variance should be apportioned (which is rarely, if ever, the case), Type I sums of squares are not recommended.
There is not a consensus about whether Type II or Type III sums of squares is to be preferred. On the one hand, if there is no interaction, then Type II sums of squares will be more powerful for two reasons:
- variance confounded between the main effect and interaction is properly assigned to the main effect and
- weighting the means by sample sizes gives better estimates of the effects.
To take advantage of the greater power of Type II sums of squares, some have suggested that if the interaction is not significant, then Type II sums of squares should be used. Maxwell and Delaney (2003) caution that such an approach could result in a Type II error in the test of the interaction. That is, it could lead to the conclusion that there is no interaction in the population when there really is one. This, in turn, would increase the Type I error rate for the test of the main effect. As a result, their general recommendation is to use Type III sums of squares.
Maxwell and Delaney (2003) recognized that some researchers prefer Type II sums of squares when there are strong theoretical reasons to suspect a lack of interaction and the p value is much higher than the typical \(α\) level of \(0.05\). However, this argument for the use of Type II sums of squares is not entirely convincing. As Tukey (1991) and others have argued, it is doubtful that any effect, whether a main effect or an interaction, is exactly \(0\) in the population. Incidentally, Tukey argued that the role of significance testing is to determine whether a confident conclusion can be made about the direction of an effect, not simply to conclude that an effect is not exactly \(0\).
Finally, if one assumes that there is no interaction, then an ANOVA model with no interaction term should be used rather than Type II sums of squares in a model that includes an interaction term. (Models without interaction terms are not covered in this book).
There are situations in which Type II sums of squares are justified even if there is strong interaction. This is the case because the hypotheses tested by Type II and Type III sums of squares are different, and the choice of which to use should be guided by which hypothesis is of interest. Recall that Type II sums of squares weight cells based on their sample sizes whereas Type III sums of squares weight all cells the same. Consider Figure \(\PageIndex{1}\) which shows data from a hypothetical \(A(2) \times B(2)\)design. The sample sizes are shown numerically and are represented graphically by the areas of the endpoints.
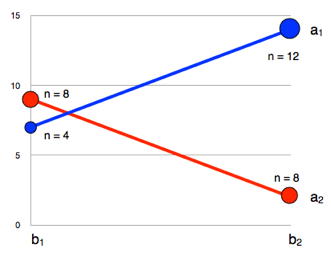
First, let's consider the hypothesis for the main effect of \(B\) tested by the Type III sums of squares. Type III sums of squares weight the means equally and, for these data, the marginal means for \(b_1\) and \(b_2\) are equal:
For \(b_1:(b_1a_1 + b_1a_2)/2 = (7 + 9)/2 = 8\)
For \(b_2:(b_2a_1 + b_2a_2)/2 = (14+2)/2 = 8\)
Thus, there is no main effect of \(B\) when tested using Type III sums of squares. For Type II sums of squares, the means are weighted by sample size.
For \(b_1: (4 \times b_1a_1 + 8 \times b_1a_2)/12 = (4 \times 7 + 8 \times 9)/12 = 8.33\)
For \(b_2: (12 \times b_2a_1 + 8 \times b_2a_2)/20 = (12 \times 14 + 8 \times 2)/20 = 9.2\)
Since the weighted marginal mean for \(b_2\) is larger than the weighted marginal mean for \(b_1\), there is a main effect of \(B\) when tested using Type II sums of squares.
The Type II and Type III analysis are testing different hypotheses. First, let's consider the case in which the differences in sample sizes arise because in the sampling of intact groups, the sample cell sizes reflect the population cell sizes (at least approximately). In this case, it makes sense to weight some means more than others and conclude that there is a main effect of \(B\). This is the result obtained with Type II sums of squares. However, if the sample size differences arose from random assignment, and there just happened to be more observations in some cells than others, then one would want to estimate what the main effects would have been with equal sample sizes and, therefore, weight the means equally. With the means weighted equally, there is no main effect of \(B\), the result obtained with Type III sums of squares.
Unweighted Means Analysis
Type III sums of squares are tests of differences in unweighted means. However, there is an alternative method to testing the same hypotheses tested using Type III sums of squares. This method, unweighted means analysis, is computationally simpler than the standard method but is an approximate test rather than an exact test. It is, however, a very good approximation in all but extreme cases. Moreover, it is exactly the same as the traditional test for effects with one degree of freedom. The Analysis Lab uses unweighted means analysis and therefore may not match the results of other computer programs exactly when there is unequal n and the df are greater than one.
Causes of Unequal Sample Sizes
None of the methods for dealing with unequal sample sizes are valid if the experimental treatment is the source of the unequal sample sizes. Imagine an experiment seeking to determine whether publicly performing an embarrassing act would affect one's anxiety about public speaking. In this imaginary experiment, the experimental group is asked to reveal to a group of people the most embarrassing thing they have ever done. The control group is asked to describe what they had at their last meal. Twenty subjects are recruited for the experiment and randomly divided into two equal groups of \(10\), one for the experimental treatment and one for the control. Following their descriptions, subjects are given an attitude survey concerning public speaking. This seems like a valid experimental design. However, of the \(10\) subjects in the experimental group, four withdrew from the experiment because they did not wish to publicly describe an embarrassing situation. None of the subjects in the control group withdrew. Even if the data analysis were to show a significant effect, it would not be valid to conclude that the treatment had an effect because a likely alternative explanation cannot be ruled out; namely, subjects who were willing to describe an embarrassing situation differed from those who were not. Thus, the differential dropout rate destroyed the random assignment of subjects to conditions, a critical feature of the experimental design. No amount of statistical adjustment can compensate for this flaw.
- Maxwell, S. E., & Delaney, H. D. (2003) Designing Experiments and Analyzing Data: A Model Comparison Perspective, Second Edition, Lawrence Erlbaum Associates, Mahwah, New Jersey.
- Tukey, J. W. (1991) The philosophy of multiple comparisons, Statistical Science, 6, 110-116.


