10.2: Two Population Means with Unknown Standard Deviations
- Page ID
- 20421
- The two independent samples are simple random samples from two distinct populations.
- For the two distinct populations:
- if the sample sizes are small, the distributions must be normal.
- if the sample sizes are large, knowing the distributions are not important.
The test comparing two independent population means with unknown and possibly unequal population standard deviations is called the Aspin-Welch \(t\)-test. The degrees of freedom formula was developed by Aspin-Welch.
The comparison of two population means is very common. A difference between the two samples depends on both the means and the standard deviations. Very different means can occur by chance if there is great variation among the individual samples. In order to account for the variation, we take the difference of the sample means, \(\bar{X}_{1} - \bar{X}_{2}\), and divide by the standard error in order to standardize the difference. The result is a t-score test statistic.
Because we do not know the population standard deviations, we estimate them using the two sample standard deviations from our independent samples. For the hypothesis test, we calculate the estimated standard deviation, or standard error, of the difference in sample means, \(\bar{X}_{1} - \bar{X}_{2}\).
The standard error is:
\[\sqrt{\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}}\]
The test statistic (t-score) is calculated as follows:
\[\dfrac{(\bar{x_{1}}-\bar{x_{2}}) - (\mu_{1} - \mu_{2})}{\sqrt{\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}}}\]
where:
- \(s_{1}\) and \(s_{2}\), the sample standard deviations, are estimates of \(\sigma_{1}\) and \(\sigma_{1}\), respectively.
- \(\sigma_{1}\) and \(\sigma_{2}\) are the unknown population standard deviations.
- \(\bar{x}_{1}\) and \(\bar{x}_{2}\) are the sample means. \(\mu_{1}\) and \(\mu_{2}\) are the population means.
The number of degrees of freedom (\(df\)) requires a somewhat complicated calculation. However, a computer or calculator calculates it easily. The \(df\) are not always a whole number. The test statistic calculated previously is approximated by the Student's t-distribution with \(df\) as follows:
Degrees of freedom
\[df = \dfrac{\left(\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}\right)^{2}}{\left(\dfrac{1}{n_{1}-1}\right)\left(\dfrac{(s_{1})^{2}}{n_{1}}\right)^{2} + \left(\dfrac{1}{n_{2}-1}\right)\left(\dfrac{(s_{2})^{2}}{n_{2}}\right)^{2}}\]
When both sample sizes \(n_{1}\) and \(n_{2}\) are five or larger, the Student's t approximation is very good. Notice that the sample variances \((s_{1})^{2}\) and \((s_{2})^{2}\) are not pooled. (If the question comes up, do not pool the variances.) It is not necessary to compute the degrees of freedom by hand. A calculator or computer easily computes it.
Two Independent Samples with Statistics Calculator
Enter in the statistics, the tail type and the confidence level and hit Calculate and the test statistic, t, the p-value, p, the confidence interval's lower bound, LB, and the upper bound, UB will be shown. Be sure to enter the confidence level as a decimal, e.g., 95% has a CL of 0.95.
| Sample Size | Sample Mean | Sample Standard Deviation | |
| First Sample | |||
| Second Sample |
|
|
| t: | p: | LB: | UB: |
Example \(\PageIndex{1}\): Independent groups
The average amount of time boys and girls aged seven to 11 spend playing sports each day is believed to be the same. A study is done and data are collected, resulting in the data in Table \(\PageIndex{1}\). Each populations has a normal distribution.
| Sample Size | Average Number of Hours Playing Sports Per Day | Sample Standard Deviation | |
|---|---|---|---|
| Girls | 9 | 2 | 0.866 |
| Boys | 16 | 3.2 | 1.00 |
Is there a difference in the mean amount of time boys and girls aged seven to 11 play sports each day? Test at the 5% level of significance.
Answer
The population standard deviations are not known. Let g be the subscript for girls and b be the subscript for boys. Then, \(\mu_{g}\) is the population mean for girls and \(\mu_{b}\) is the population mean for boys. This is a test of two independent groups, two population means.
Random variable: \(\bar{X}_{g} - \bar{X}_{b} =\) difference in the sample mean amount of time girls and boys play sports each day.
- \(H_{0}: \mu_{g} = \mu_{b}\ \) or \(\mu_{g} - \mu_{b} = 0\)
- \(H_{a}: \mu_{g} \neq \mu_{b} \) or \( \mu_{g} - \mu_{b} \neq 0\)
The words "the same" tell you \(H_{0}\) has an "=". Since there are no other words to indicate \(H_{a}\), assume it says "is different." This is a two-tailed test.
Distribution for the test: Use \(t_{df}\) where \(df\) is calculated using the \(df\) formula for independent groups, two population means. Using a calculator, \(df\) is approximately 18.8462. Do not pool the variances.
Calculate the test statistic and the p-value using a Student's t-distribution: \(t = -3.1424 \), \(p\text{-value} = 0.0054\)
Graph:
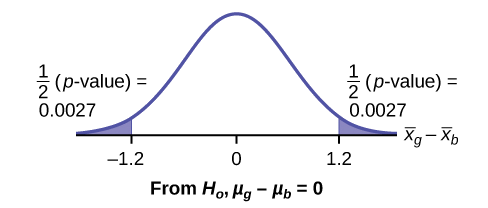
\[s_{g} = 0.866\]
\[s_{b} = 1\]
So,
\[\bar{x}_{g} - \bar{x}_{b} = 2 - 3.2 = -1.2\]
Half the \(p\text{-value}\) is below –1.2 and half is above 1.2.
Make a decision: Since \(\alpha > p\text{-value}\), reject \(H_{0}\). This means you reject \(\mu_{g} = \mu_{b}\). The means are different.
Go to the Two Independent Samples With Statistics calculator.
Fill in the table:
First Sample Sample size = 9, First Sample Sample Mean = 2, First Sample Standard Deviation = 0.866
Second Sample Sample size = 16, Second Sample Sample Mean = 3.2, Second Sample Standard Deviation = 1.00
Check "\(\neq\)" and click Calculate.
The \(p\text{-value}\) is \(p = 0.0054\).
Conclusion: At the 5% level of significance, the sample data show there is sufficient evidence to conclude that the population mean number of hours that girls and boys aged seven to 11 play sports per day is different (population mean number of hours boys aged seven to 11 play sports per day is greater than the population mean number of hours played by girls OR the population mean number of hours girls aged seven to 11 play sports per day is greater than the population mean number of hours played by boys).
Exercise 10.2.1
Two samples are shown in Table \(\PageIndex{2}\) . Both have normal distributions. The means for the two populations are thought to be the same. Is there a difference in the means? Test at the 5% level of significance.
| Sample Size | Sample Mean | Sample Standard Deviation | |
|---|---|---|---|
| Population A | 25 | 5 | 1 |
| Population B | 16 | 4.7 | 1.2 |
Answer
The \(p\text{-value}\) is \(0.4125\), which is much higher than 0.05, so we decline to reject the null hypothesis. There is not sufficient evidence to conclude that the means of the two populations are not the same.
Note on Sample Sizes:
When the sum of the sample sizes is larger than \(30 (n_{1} + n_{2} > 30)\) you can use the normal distribution to approximate the Student's \(t\).
Example \(\PageIndex{2}\)
A study is done by a community group in two neighboring colleges to determine which one graduates students with more math classes. College A samples 11 graduates. Their average is four math classes with a standard deviation of 1.5 math classes. College B samples nine graduates. Their average is 3.5 math classes with a standard deviation of one math class. The community group believes that a student who graduates from college A has taken more math classes, on the average. Both populations have a normal distribution. Test at a 1% significance level. Answer the following questions.
- Is this a test of two means or two proportions?
- Are the populations standard deviations known or unknown?
- Which distribution do you use to perform the test?
- What is the random variable?
- What are the null and alternate hypotheses? Write the null and alternate hypotheses in words and in symbols.
- Is this test right-, left-, or two-tailed?
- What is the \(p\text{-value}\)?
- Do you reject or not reject the null hypothesis?
Solutions
- two means
- unknown
- Student's t
- \(\bar{X}_{A} - \bar{X}_{B}\)
- \(H_{0}: \mu_{A} = \mu_{B}\) and \(H_{a}: \mu_{A} > \mu_{B}\)
-
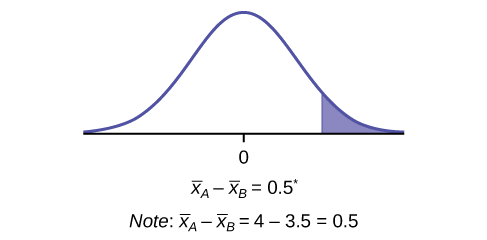
Figure 10.2.2.
Therefore, it is a right-tailed test.
- 0.1928
- Do not reject.
- At the 1% level of significance, from the sample data, there is not sufficient evidence to conclude that a student who graduates from college A has taken more math classes, on the average, than a student who graduates from college B.
Exercise \(\PageIndex{2}\)
A study is done to determine if Company A retains its workers longer than Company B. Company A samples 15 workers, and their average time with the company is five years with a standard deviation of 1.2. Company B samples 20 workers, and their average time with the company is 4.5 years with a standard deviation of 0.8. The populations are normally distributed.
- Are the population standard deviations known?
- Conduct an appropriate hypothesis test. At the 5% significance level, what is your conclusion?
Answer
- They are unknown.
- The \(p\text{-value} = 0.0878\). At the 5% level of significance, there is insufficient evidence to conclude that the workers of Company A stay longer with the company.
Two Independent Samples with data Calculator
Type in the values from the two data sets separated by commas, for example, 2,4,5,8,11,2. Then enter the tail type and the confidence level and hit Calculate and the test statistic, t, the p-value, p, the confidence interval's lower bound, LB, and the upper bound, UB will be shown. Be sure to enter the confidence level as a decimal, e.g., 95% has a CL of 0.95.
Data1:
Data2:
|
CL: |
| t: | p | LB | UB |
Example \(\PageIndex{3}\)
A professor at a large community college wanted to determine whether there is a difference in the means of final exam scores between students who took his statistics course online and the students who took his face-to-face statistics class. He believed that the mean of the final exam scores for the online class would be lower than that of the face-to-face class. Was the professor correct? The randomly selected 30 final exam scores from each group are listed in Table \(\PageIndex{3}\) and Table \(\PageIndex{4}\).
| 67.6 | 41.2 | 85.3 | 55.9 | 82.4 | 91.2 | 73.5 | 94.1 | 64.7 | 64.7 |
| 70.6 | 38.2 | 61.8 | 88.2 | 70.6 | 58.8 | 91.2 | 73.5 | 82.4 | 35.5 |
| 94.1 | 88.2 | 64.7 | 55.9 | 88.2 | 97.1 | 85.3 | 61.8 | 79.4 | 79.4 |
| 77.9 | 95.3 | 81.2 | 74.1 | 98.8 | 88.2 | 85.9 | 92.9 | 87.1 | 88.2 |
| 69.4 | 57.6 | 69.4 | 67.1 | 97.6 | 85.9 | 88.2 | 91.8 | 78.8 | 71.8 |
| 98.8 | 61.2 | 92.9 | 90.6 | 97.6 | 100 | 95.3 | 83.5 | 92.9 | 89.4 |
Is the mean of the Final Exam scores of the online class lower than the mean of the Final Exam scores of the face-to-face class? Test at a 5% significance level. Answer the following questions:
- Is this a test of two means or two proportions?
- Are the population standard deviations known or unknown?
- Which distribution do you use to perform the test?
- What is the random variable?
- What are the null and alternative hypotheses? Write the null and alternative hypotheses in words and in symbols.
- Is this test right, left, or two tailed?
- What is the \(p\text{-value}\)?
- Do you reject or not reject the null hypothesis?
- At the ___ level of significance, from the sample data, there ______ (is/is not) sufficient evidence to conclude that ______.
(See the conclusion in Example, and write yours in a similar fashion)
Be careful not to mix up the information for Group 1 and Group 2!
Answer
- two means
- unknown
- Student's \(t\)
- \(\bar{X}_{1} - \bar{X}_{2}\)
-
- \(H_{0}: \mu_{1} = \mu_{2}\) Null hypothesis: the means of the final exam scores are equal for the online and face-to-face statistics classes.
- \(H_{a}: \mu_{1} < \mu_{2}\) Alternative hypothesis: the mean of the final exam scores of the online class is less than the mean of the final exam scores of the face-to-face class.
- left-tailed
- \(p\text{-value} = 0.0011\)
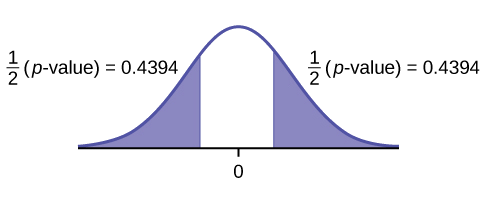
Figure 10.2.3.
- Reject the null hypothesis
- The professor was correct. The evidence shows that the mean of the final exam scores for the online class is lower than that of the face-to-face class.
At the 5% level of significance, from the sample data, there is (is/is not) sufficient evidence to conclude that the mean of the final exam scores for the online class is less than the mean of final exam scores of the face-to-face class.
First put the data for each group into two lists (such as L1 and L2). Press STAT. Arrow over to TESTS and press 4:2SampTTest. Make sure Data is highlighted and press ENTER. Arrow down and enter L1 for the first list and L2 for the second list. Arrow down to \(\mu_{1}\): and arrow to \(\neq \mu_{1}\) (does not equal). Press ENTER. Arrow down to Pooled: No. Press ENTER. Arrow down to Calculate and press ENTER.
Confidence Intervals for the Difference Between Two Population Means (Independent Samples)
Hypothesis tests are used to provide evidence that one population mean is larger, smaller, or different from another population mean. Recall that if the interest is to estimate how much larger a population mean is from a given value, then a confidence interval is used. In same way that confidence intervals for a population mean is constructed, a confidence interval for the difference between two population means can also be constructed if the samples are independent of each other. The center of the confidence interval will be the difference between the sample means and the margin of error will be the product of the corresponding value of t and the standard error. Putting this together gives the following formula.
Confidence Interval for the Difference Formula
\(\left(\bar{x_2}-\bar{x_1}-t_{\frac{\alpha}{2}}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}},\bar{x_2}-\bar{x_1}+t_{\frac{\alpha}{2}}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}\right)\)
Although one can always theoretically use the formula, in practical applications technology is used. The computer calculators built into this section compute the confidence interval without too much difficulty.
Example \(\PageIndex{4}\)
It is well known that college graduates make more money on average than students who do not graduate from college, but a college was interested in how much more money on average their graduates made compared to those who did not complete their degree. Notice that a confidence interval rather than a hypothesis test will be helpful in providing information about this. Suppose a college tracked a total of 300 students who entered the college. 242 of these students successfully completed their degree and ten years after they entered college their mean salary was $72,148 and their standard deviation was $22,263. The 58 students who did not successfully complete their degree had a mean salary of $47,972 ten years after they entered the college and their standard deviation was $16,845.
Answer the following questions:
- Is this a confidence interval for the difference of two means or two proportions?
- Are the population standard deviations known or unknown?
- Which distribution do you use to perform the test?
- What is the random variable?
- What is the lower bound for the 95% confidence interval?
- What is the upper bound for the 95% confidence interval?
- State and interpret the 95% confidence interval.
- Interpret the lower bound for the 95% confidence interval.
- Interpret the upper bound for the 95% confidence interval.
- Explain what it means to be 95% confident in the context of the study.
Answer
- two means
- unknown
- Student's \(t\)
- \(\bar{X}_{1} - \bar{X}_{2}\)
- 18,955
- 29,397
- The 95% confidence interval is [18955, 29397]. With 95% confidence, the population mean salary ten years after entering college is between $18,955 and 29,397 higher for those who successfully complete their degree compared to those who do not complete their degree.
- With 95% confidence, we can state that ten years after entering college, those who complete their degree, on average, make at least $18,955 more money per year than those who do not complete their degree.
- With 95% confidence, we can state that ten years after entering college, those who complete their degree, on average, have a salary that is at most $29,397 higher than those who do not complete their degree.
- If many samples of 242 students who completed their degree and 58 students who did not complete their degree were looked at, then a different confidence interval would result from each of these samples. 95% of these confidence intervals will contain the true population mean difference in salaries and 5% of these confidence intervals will fail to contain the true population mean difference in salaries.
Exercise \(\PageIndex{5}\)
How much more exercise do Californians (CA) get each week compared to Alabamians (AL)? The table below shows the results of a study on exercise. Assume that the distributions of exercise time are normal for both California and Alabama. Come up with and interpret the 90% confidence interval for the difference.
| CA | 162 | 134 | 97 | 168 | 88 | 72 | 297 | 141 | 130 |
| AL | 37 | 111 | 28 | 75 | 92 | 187 | 12 | 62 |
Answer
The 90% confidence interval is [15.74, 119.71]. With 90% confidence it can be concluded that the population mean amount of exercise that Californians get each week is between 15.74 and 119.71 minutes longer than the population mean amount of exercise that Alabamians get each week.
Cohen's Standards for Small, Medium, and Large Effect Sizes
Note: Cohen's Standards are covered in relatively few elementary statistic classes, so this topic may be optional
Cohen's \(d\) is a measure of effect size based on the differences between two means. Cohen’s \(d\), named for United States statistician Jacob Cohen, measures the relative strength of the differences between the means of two populations based on sample data. The calculated value of effect size is then compared to Cohen’s standards of small, medium, and large effect sizes.
| Size of effect | \(d\) |
|---|---|
| Small | 0.2 |
| medium | 0.5 |
| Large | 0.8 |
Cohen's \(d\) is the measure of the difference between two means divided by the pooled standard deviation: \(d = \dfrac{\bar{x}_{2}-\bar{x}_{2}}{s_{\text{pooled}}}\) where \(s_{pooled} = \sqrt{\dfrac{(n_{1}-1)s^{2}_{1} + (n_{2}-1)s^{2}_{2}}{n_{1}+n_{2}-2}}\)
Example \(\PageIndex{6}\)
Calculate Cohen’s d for Example. Is the size of the effect small, medium, or large? Explain what the size of the effect means for this problem.
Answer
\(\mu_{1} = 4 s_{1} = 1.5 n_{1} = 11\)
\(\mu_{2} = 3.5 s_{2} = 1 n_{2} = 9\)
\(d = 0.384\)
The effect is small because 0.384 is between Cohen’s value of 0.2 for small effect size and 0.5 for medium effect size. The size of the differences of the means for the two colleges is small indicating that there is not a significant difference between them.
Example \(\PageIndex{7}\)
Calculate Cohen’s \(d\) for Example. Is the size of the effect small, medium or large? Explain what the size of the effect means for this problem.
Answer
\(d = 0.834\); Large, because 0.834 is greater than Cohen’s 0.8 for a large effect size. The size of the differences between the means of the Final Exam scores of online students and students in a face-to-face class is large indicating a significant difference.
Example 10.2.8
Weighted alpha is a measure of risk-adjusted performance of stocks over a period of a year. A high positive weighted alpha signifies a stock whose price has risen while a small positive weighted alpha indicates an unchanged stock price during the time period. Weighted alpha is used to identify companies with strong upward or downward trends. The weighted alpha for the top 30 stocks of banks in the northeast and in the west as identified by Nasdaq on May 24, 2013 are listed in Table and Table, respectively.
| 94.2 | 75.2 | 69.6 | 52.0 | 48.0 | 41.9 | 36.4 | 33.4 | 31.5 | 27.6 |
| 77.3 | 71.9 | 67.5 | 50.6 | 46.2 | 38.4 | 35.2 | 33.0 | 28.7 | 26.5 |
| 76.3 | 71.7 | 56.3 | 48.7 | 43.2 | 37.6 | 33.7 | 31.8 | 28.5 | 26.0 |
| 126.0 | 70.6 | 65.2 | 51.4 | 45.5 | 37.0 | 33.0 | 29.6 | 23.7 | 22.6 |
| 116.1 | 70.6 | 58.2 | 51.2 | 43.2 | 36.0 | 31.4 | 28.7 | 23.5 | 21.6 |
| 78.2 | 68.2 | 55.6 | 50.3 | 39.0 | 34.1 | 31.0 | 25.3 | 23.4 | 21.5 |
Is there a difference in the weighted alpha of the top 30 stocks of banks in the northeast and in the west? Test at a 5% significance level. Answer the following questions:
- Is this a test of two means or two proportions?
- Are the population standard deviations known or unknown?
- Which distribution do you use to perform the test?
- What is the random variable?
- What are the null and alternative hypotheses? Write the null and alternative hypotheses in words and in symbols.
- Is this test right, left, or two tailed?
- What is the \(p\text{-value}\)?
- Do you reject or not reject the null hypothesis?
- At the ___ level of significance, from the sample data, there ______ (is/is not) sufficient evidence to conclude that ______.
- Calculate Cohen’s d and interpret it.
Answer
- two means
- unknown
- Student’s-t
- \(\bar{X}_{1} - \bar{X}_{2}\)
-
- \(H_{0}: \mu_{1} = \mu_{2}\) Null hypothesis: the means of the weighted alphas are equal.
- \(H_{a}: \mu_{1} \neq \mu_{2}\) Alternative hypothesis : the means of the weighted alphas are not equal.
- two-tailed
- \(p\text{-value} = 0.8787\)
- Do not reject the null hypothesis
- This indicates that the trends in stocks are about the same in the top 30 banks in each region.

Figure 10.2.4.
5% level of significance, from the sample data, there is not sufficient evidence to conclude that the mean weighted alphas for the banks in the northeast and the west are different - \(d = 0.040\), Very small, because 0.040 is less than Cohen’s value of 0.2 for small effect size. The size of the difference of the means of the weighted alphas for the two regions of banks is small indicating that there is not a significant difference between their trends in stocks.
References
- Data from Graduating Engineer + Computer Careers. Available online at http://www.graduatingengineer.com
- Data from Microsoft Bookshelf.
- Data from the United States Senate website, available online at www.Senate.gov (accessed June 17, 2013).
- “List of current United States Senators by Age.” Wikipedia. Available online at http://en.Wikipedia.org/wiki/List_of...enators_by_age (accessed June 17, 2013).
- “Sectoring by Industry Groups.” Nasdaq. Available online at http://www.nasdaq.com/markets/barcha...&base=industry (accessed June 17, 2013).
- “Strip Clubs: Where Prostitution and Trafficking Happen.” Prostitution Research and Education, 2013. Available online at www.prostitutionresearch.com/ProsViolPosttrauStress.html (accessed June 17, 2013).
- “World Series History.” Baseball-Almanac, 2013. Available online at http://www.baseball-almanac.com/ws/wsmenu.shtml (accessed June 17, 2013).
Chapter Review
Two population means from independent samples where the population standard deviations are not known
- Random Variable: \(\bar{X}_{1} - \bar{X}_{2} =\) the difference of the sampling means
- Distribution: Student's t-distribution with degrees of freedom (variances not pooled)
Formula Review
Standard error: \[SE = \sqrt{\dfrac{(s_{1}^{2})}{n_{1}} + \dfrac{(s_{2}^{2})}{n_{2}}}\]
Test statistic (t-score): \[t = \dfrac{(\bar{x}_{1}-\bar{x}_{2}) - (\mu_{1}-\mu_{2})}{\sqrt{\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}}}\]
Degrees of freedom:
\[df = \dfrac{\left(\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}\right)^{2}}{\left(\dfrac{1}{n_{1} - 1}\right)\left(\dfrac{(s_{1})^{2}}{n_{1}}\right)^{2} + \left(\dfrac{1}{n_{2} - 1}\right)\left(\dfrac{(s_{2})^{2}}{n_{2}}\right)^{2}}\]
where:
- \(s_{1}\) and \(s_{2}\) are the sample standard deviations, and n1 and n2 are the sample sizes.
- \(x_{1}\) and \(x_{2}\) are the sample means.
Confidence Interval:
\(\left(\bar{x_2}-\bar{x_1}-t_{\frac{\alpha}{2}}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}},\bar{x_2}-\bar{x_1}+t_{\frac{\alpha}{2}}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}\right)\)
Cohen’s \(d\) is the measure of effect size:
\[d = \dfrac{\bar{x}_{1} - \bar{x}_{2}}{s_{\text{pooled}}}\]
where
\[s_{\text{pooled}} = \sqrt{\dfrac{(n_{1} - 1)s^{2}_{1} + (n_{2} - 1)s^{2}_{2}}{n_{1} + n_{2} - 2}}\]
Glossary
- Degrees of Freedom (\(df\))
- the number of objects in a sample that are free to vary.
- Standard Deviation
- A number that is equal to the square root of the variance and measures how far data values are from their mean; notation: \(s\) for sample standard deviation and \(\sigma\) for population standard deviation.
- Variable (Random Variable)
- a characteristic of interest in a population being studied. Common notation for variables are upper-case Latin letters \(X, Y, Z,\)... Common notation for a specific value from the domain (set of all possible values of a variable) are lower-case Latin letters \(x, y, z,\).... For example, if \(X\) is the number of children in a family, then \(x\) represents a specific integer 0, 1, 2, 3, .... Variables in statistics differ from variables in intermediate algebra in two following ways.
- The domain of the random variable (RV) is not necessarily a numerical set; the domain may be expressed in words; for example, if \(X =\) hair color, then the domain is {black, blond, gray, green, orange}.
- We can tell what specific value x of the random variable \(X\) takes only after performing the experiment.
Contributors and Attributions
Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/30189442-699...b91b9de@18.114.


