Ch 11.1 Chi-square Distribution
- Page ID
- 15930
Ch 11.1 Facts about Chi-square distribution
Notation for chi-square distribution is χ2 . It is a distribution with degree of freedom (df = n -1).
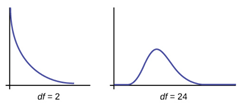
Characteristic of chi-square distribution.
i) Shape of the distribution is right skew,
non-symmetrical. There is a different chi-square curve for each df. When df > 90, the chi-square curve approximates the normal distribution.
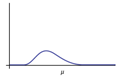
ii) mean μ = df (n-1), σ = \( 2 \sqrt{df} \). The mean is located just right of the peak.
iii) ![]() = sum of (n-1) independent, standard normal variable. χ2 is always positive.
= sum of (n-1) independent, standard normal variable. χ2 is always positive.
Chi-square distribution calculator:
http://onlinestatbook.com/2/calculators/chi_square_prob.html
The calculator can be used to find area to the right of a chi-square value P( χ2 > a)
Ex. Find probability that χ2 is greater than 31 when
df = 10.
Enter chi-square = 31, df = 10, calculate.

