Ch 8.3 Confidence Interval for Population Proportion
- Page ID
- 15923
Ch 8.3 Confidence Interval for population proportion:
Terms: Population proportion: p
Sample proportion: \( \hat{p} \) = (x/n)
Number of success: x; sample size: n
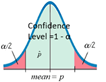
Confidence Level: C-level
Significant Level: α = 1 – C-level (probability of unlikely)
EBP: Error Bound for proportion, margin of error
A) To Estimate p:
\( \fbox {1) point estimate: \( \hat{p} = x/n \) } \)
\( \fbox{ 2) Interval estimate: \( \hat{p} - E \text{ to } \hat{p} + E \) } \)
\( E(EBP) = z_ {\alpha /2} \sqrt{\frac{\hat{p}\hat{q}}{n}} \)
Note: E is the approximated value of sampling error of sampling distribution of \( \hat{p} \), which has a normal distribution when x and n-x ≥ 5.
Use Statdisk online calculator to find the confidence interval.
- identify C-level, sample size n and success = x.
- https://www.statdisk.com/# , Analysis/ Confidence Intervals/Proportion one sample/
output: E (EBP) and lower < p < upper
\( z_ {\alpha /2} \) is the critical value with C-level in the middle.
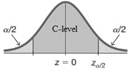 To find \( z_ {\alpha /2} \)
To find \( z_ {\alpha /2} \)
Use online Inverse Normal calculator, set area = \( \alpha /2 \), mean = 0, sd =1,
click above, recalculate.
Explanation:
X = number of success is a binomial distribution with mean = np and sd = \( \sqrt{npq} \).
When np and nq ≥ 5, distribution of X is normal with mean = np and sd = \( \sqrt{npq} \) .
So distribution of \( \hat{p} = \frac{x}{n} \) is normal with mean = p and SD = \( \sqrt{\frac{\hat{p}\hat{q}}{n}} \) .
At a given C-level, the maximum error of \( \hat{p} \) and p is E where \( E(EBP) = z_ {\alpha /2} \sqrt{\frac{\hat{p}\hat{q}}{n}} \)
Note: the requirement for this confidence interval is not n > 30 but np and nq ≥ 5.
Interpret a 95% Confidence Interval:
We are 95% confidence that the interval from ____ to ____ actual contain the true value of the population proportion of the category of interest.
The Confidence interval also shows that 95% of all confidence Intervals contain the true value of p.
Make conclusion from confidence interval:
1) Any value in the confidence Interval can be p.
2) If the whole interval > a, we can conclude p > a
3) If the whole interval < a, we can conclude p < a.
4) When two confidence interval overlap, we can conclude that the two p may be the same. We cannot conclude one of the p is higher.
Ex1. A research is conducted to determine how many household use Netflix to stream videos. A random sample of 500 households show that 442 households use Netflix.
a) Use a 90% confidence level to compute a confidence interval estimate of true proportion of households using Netflix.
use Statdisk Analysis/Confidence Intervals/Proportion one sample : Clevel = 0.9, n = 500, x = 442,
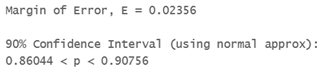
b) Find the critical value.
Use Inverse Normal calculator, since clevel = 90%, \( \alpha = 0.1, \alpha /2 = 0.05 \), set area = 0.05, mean = 0, sd = 1,
click above, recalculate.
\( z_ {\alpha /2} \) = 1.645
c) Interpret the confidence interval in non-technical term.
We estimate with 90% confidence that the true proportion of all households that use Netflix is between 86.0% to 90.8%
d) Can we conclude with 90% confidence that more than 80% of households use Netflix?
Since the interval contains 86.0% to 90.8%, all values are more than 80%, so we can conclude that.
Ex2: A Gallup poll of 1487 adults showed that 43% of the respondents have Facebook pages.
a) Find the number in the sample who have Facebook pages. \( x = n(\hat{p}) \) = 1487 (0.43) = 639
c) Find the interval estimate of p at 95% confidence level and margin of error E.
Use statdisk with Clevel = 0.95, n = 1487, x = 639
Interval estimate is 0.405 < p < 0.455, E = 0.025
d) Write a non-technical interpretation of the above
We are 95% confidence that the true percent of adults who have Facebook pages are between 40.5% to 45.5%.
e) Can we claim that less than 60% of all adults have Facebook pages?
Since the whole interval is less than 0.6, yes, we can conclude less than 60% of all adults have Facebook pages.
B) Determine sample size for a desired E
Since \( E(EBP) = z_ {\alpha /2} \sqrt{\frac{\hat{p}\hat{q}}{n}} \)
\( n = \frac{(z_ {\alpha/2})^2\hat{p}\hat{q}}{E^2} \) when an estimate \( \hat{p} \) is known.
\( n = \frac{(z_ {\alpha/2})^2\cdot 0.25}{E^2} \) when no estimate \( \hat{p} \) is known.
Use statdisk / Analysis/Sample size Determination/ Estimate proportion to find sample size for a given error E.
Input C-Level, Desired E, Estimate of p = \( \hat{p} = \frac{x}{n} \), evaluate.
Ex3. What sample size should be used if we want the keep the margin of error within 2.1% when estimating a proportion at a 90% confidence interval. use \(\hat{p} = 0.43 \) as an old estimation of p.
C-level = 0.9, E = 0.021, estimate of p = 0.43, Evaluate
Sample size p = 1504.
b) If no previous study has been done , what sample size will be needed. (do not use p-hat = 0.43)
Use statdisk / Analysis/Sample size Determination/ Estimate proportion
C-level = 0.9, E = 0.021, estimate of p = blank, evaluate
sample size p = 1534

