3.4: Joint Distributions
- Page ID
- 10144
The purpose of this section is to study how the distribution of a pair of random variables is related to the distributions of the variables individually. If you are a new student of probability you may want to skip the technical details.
Basic Theory
Joint and Marginal Distributions
As usual, we start with a random experiment modeled by a probability space \((\Omega, \mathscr F, \P)\). So to review, \(\Omega\) is the set of outcomes, \(\mathscr F\) is the collection of events, and \(\P\) is the probability measure on the sample space \((\Omega, \mathscr F)\). Suppose now that \(X\) and \(Y\) are random variables for the experiment, and that \(X\) takes values in \(S\) while \(Y\) takes values in \(T\). We can think of \((X, Y)\) as a random variable taking values in the product set \(S \times T\). The purpose of this section is to study how the distribution of \((X, Y)\) is related to the distributions of \(X\) and \(Y\) individually.
Recall that
- The distribution of \((X, Y)\) is the probability measure on \(S \times T\) given by \(\P\left[(X, Y) \in C\right] \) for \(C \subseteq S \times T\).
- The distribution of \(X\) is the probability measure on \(S\) given by \(\P(X \in A) \) for \( A \subseteq S \).
- The distribution of \( Y \) is the probability measure on \(T\) given by \(\P(Y \in B) \) for \( B \subseteq T \).
In this context, the distribution of \((X, Y)\) is called the joint distribution, while the distributions of \(X\) and of \(Y\) are referred to as marginal distributions.
Details
The sets \(S\) and \(T\) come with \(\sigma\)-algebras of admissible subssets \(\mathscr S\) and \(\mathscr T\), respectively, just as the collection of events \(\mathscr F\) is a \(\sigma\)-algebra. The Cartesian product set \(S \times T\) is given the product \(\sigma\)-algebra \(\mathscr S \otimes \mathscr T\) generated by products \(A \times B\) where \(A \in \mathscr S\) and \(B \in \mathscr T\). The random variables \(X\) and \(Y\) are measurable, which ensures that \((X, Y)\) is also a random variable (that is, measurable). Moreover, the distribution of \((X, Y)\) is uniquely determined by probabilities of the form \(\P[(X, Y) \in A \times B] = \P(X \in A, Y \in B)\) where \(A \in \mathscr S\) and \(B \in \mathscr T\). As usual the spaces \( (S, \mathscr S) \) and \( (T, \mathscr T) \) each fall into the two classes we have studied in the previous sections:
- Discrete: the set is countable and the \( \sigma \)-algebra consists of all subsets.
- Euclidean: the set is a measurable subset of \( \R^n \) for some \( n \in \N_+ \) and the \( \sigma \)-algebra consists of the measurable subsets.
The first simple but very important point, is that the marginal distributions can be obtained from the joint distribution.
Note that
- \(\P(X \in A) = \P\left[(X, Y) \in A \times T\right]\) for \(A \subseteq S\)
- \(\P(Y \in B) = \P\left[(X, Y) \in S \times B\right]\) for \(B \subseteq T\)
The converse does not hold in general. The joint distribution contains much more information than the marginal distributions separately. However, the converse does hold if \(X\) and \(Y\) are independent, as we will show below.
Joint and Marginal Densities
Recall that probability distributions are often described in terms of probability density functions. Our goal is to study how the probability density functions of \( X \) and \( Y \) individually are related to probability density function of \( (X, Y) \). But first we need to make sure that we understand our starting point.
We assume that \( (X, Y) \) has density function \( f: S \times T \to (0, \infty) \) in the following sense:
- If \( X \) and \( Y \) have discrete distributions on the countable sets \( S \) and \( T \) respectively, then \( f \) is defined by \[f(x, y) = \P(X = x, Y = y), \quad (x, y) \in S \times T\]
- If \( X \) and \( Y \) have continuous distributions on \( S \subseteq \R^j \) and \( T \subseteq \R^k \) respectively, then \( f \) is defined by the condition \[\P[(X, Y) \in C] = \int_C f(x, y) \, d(x, y), \quad C \subseteq S \times T\]
- In the mixed case where \( X \) has a discrete distribution on the countable set \( S \) and \( Y \) has a continuous distribution on \( T \subseteq R^k \), then \( f \) is defined by the condition \[ \P(X = x, Y \in B) = \int_B f(x, y) \, dy, \quad x \in S, \; B \subseteq T \]
- In the mixed case where \( X \) has a continuous distribution on \( S \subseteq \R^j \) and \( Y \) has a discrete distribution on the countable set \( T \), then \( f \) is defined by the condition \[ \P(X \in A, Y = y) = \int_A f(x, y), \, dx, \quad A \subseteq S, \; y \in T\]
Details
- In this case, \( (X, Y) \) has a discrete distribution on the countable set \( S \times T \) and \( f \) is the density function with respect to counting measure \( \# \) on \( S \times T \).
- In this case, \( (X, Y) \) has a continuous distribution on \( S \times T \subseteq \R^{j+k} \) and \( f \) is the density function with respect to Lebesgue measure \( \lambda_{j+k} \) on \( S \times T \). Lebesgue measure, named for Henri Lebesgue is the standard measure on Euclidean spaces.
- In this case, \( (X, Y) \) actually has a continuous distribution: \[ \P[(X, Y) = (x, y) = \P(X = x, Y = y) \le \P(Y = y) = 0, \quad (x, y) \in S \times T \] The function \( f \) is the density function with respect to the product measure formed from counting measure \( \# \) on \( S \) and Lebesgue measure \( \lambda_k \) on \( T \).
- This case is just like (c) but with the roles of \( S \) and \( T \) reversed. Once again, \( (X, Y) \) has a continuous distribution and \( f \) is the density function with respect to the product measure on \( S \times T \) formed by Lebesgue measure \( \lambda_j \) on \( S \) and counting measure \( \# \) on \( T \).
In cases (b), (c), and (d), the existence of a probability density function is not guaranteed, but is an assumption that we are making. All four cases (and many others) can be unified under the general theories of measure and integration.
First we will see how to obtain the probability density function of one variable when the other has a discrete distribution.
Suppose that \((X, Y)\) has probability density function \(f\) as described above.
- If \( Y \) has a discrete distribution on the countable set \( T \), then \( X \) has probability density function \( g \) given by \(g(x) = \sum_{y \in T} f(x, y)\) for \(x \in S\)
- If \( X \) has a discrete distribution on the countable set \( S \), then \( Y \) has probability density function \( h \) given by \(h(y) = \sum_{x \in S} f(x, y), \quad y \in T\)
Proof
The two results are symmetric, so we will prove (a). The main tool is the countable additivity property of probability. Suppose first that \( X \) also has a discrete distribution on the countable set \( S \). Then for \( x \in S \), \[ g(x) = \P(X = x) = \P(X = x, Y \in T) = \sum_{y \in T} \P(X = x, Y = y) = \sum_{y \in T} f(x, y) \] Suppose next that \( X \) has a continuous distribution on \( S \subseteq \R^j \). Then for \( A \subseteq \R^j \), \[ \P(X \in A) = \P(X \in A, Y \in T) = \sum_{y \in T} \P(X \in A, Y = y) = \sum_{y \in T} \int_A f(x, y) \, dx = \int_A \sum_{y \in T} f(x, y), \, dx \] The interchange of sum and integral is allowed since \( f \) is nonnegative. By the meaning of the term, \( X \) has probability density function \( g \) given by \( g(x) = \sum_{y \in T} f(x, y) \) for \( x \in S \)
Next we will see how to obtain the probability density function of one variable when the other has a continuous distribution.
Suppose again that \((X, Y)\) has probability density function \(f\) as described above.
- If \( Y \) has a continuous distribution on \( T \subseteq \R^k \) then \( X \) has probability density function \( g \) given by \(g(x) = \int_T f(x, y) \, dy, \quad x \in S\)
- If \( X \) has a continuous distribution on \( S \subseteq \R^k \) then \( Y \) has probability density function \( h \) given by \(h(y) = \int_S f(x, y) \, dx, \quad y \in T\)
Proof
Again, the results are symmetric, so we show (a). Suppose first that \( X \) has a discrete distribution on the countable set \( S \). Then for \( x \in S \) \[ g(x) = \P(X = x) = \P(X = x, Y \in T) = \int_T f(x, y) \, dy \] Next suppose that \( X \) has a continuous distribution on \( S \subseteq \R^j \). Then for \( A \subseteq S \), \[ \P(X \in A) = \P(X \in A, Y \in T) = \P\left[(X, Y) \in A \times T\right] = \int_{A \times T} f(x, y) \, d(x, y) = \int_A \int_T f(x, y) \, dy \] Hence by the very meaning of the term, \( X \) has probability density function \( g \) given by \( g(x) = \int_T f(x, y) \, dy \) for \( x \in S \). Writing the double integral as an iterated integral is a special case of Fubini's theorem, named for Guido Fubini.
In the context of the previous two theorems, \(f\) is called the joint probability density function of \((X, Y)\), while \(g\) and \(h\) are called the marginal density functions of \(X\) and of \(Y\), respectively. Some of the computational exercises below will make the term marginal clear.
Independence
When the variables are independent, the marginal distributions determine the joint distribution.
If \(X\) and \(Y\) are independent, then the distribution of \(X\) and the distribution of \(Y\) determine the distribution of \((X, Y)\).
Proof
If \(X\) and \(Y\) are independent then, \[\P\left[(X, Y) \in A \times B\right] = \P(X \in A, Y \in B) = \P(X \in A) \P(Y \in B) \quad A \in \mathscr S, \, B \in \mathscr T \] and as noted in the details for (1), this completely determines the distribution \((X, Y)\) on \(S \times T\).
When the variables are independent, the joint density is the product of the marginal densities.
Suppose that \(X\) and \(Y\) are independent and have probability density function \( g \) and \( h \) respectively. Then \((X, Y)\) has probability density function \(f\) given by \[f(x, y) = g(x) h(y), \quad (x, y) \in S \times T\]
Proof
The main tool is the fact that an event defined in terms of \( X \) is independent of an event defined in terms of \( Y \).
- Suppose that \( X \) and \( Y \) have discrete distributions on the countable sets \( S \) and \( T \) respectively. Then for \( (x, y) \in S \times T \), \[ \P\left[(X, Y) = (x, y)\right] = \P(X = x, Y = y) = \P(X = x) \P(Y = y) = g(x) h(y) \]
- Suppose next that \( X \) and \( Y \) have continuous distributions on \( S \subseteq \R^j \) and \( T \subseteq \R^k \) respectively. Then for \( A \subseteq S \) and \( B \subseteq T \). \[ \P\left[(X, Y) \in A \times B\right] = \P(X \in A, Y \in B) = \P(X \in A) \P(Y \in B) = \int_A g(x) \, dx \, \int_B h(y) \, dy = \int_{A \times B} g(x) h(y) \, d(x, y) \] As noted in the details for (1), a probability measure on \( S \times T \) is completely determined by its values on product sets, so it follows that \(\P\left[(X, Y) \in C\right] = \int_C f(x, y) \, d(x, y)\) for general \(C \subseteq S \times T\). Hence \( (X, Y) \) has PDF \( f \).
- Suppose next that \( X \) has a discrete distribution on the countable set \( S \) and that \( Y \) has a continuous distribution on \( T \subseteq \R^k \). If \( x \in S \) and \( B \subseteq T \), \[ \P(X = x, Y \in B) = \P(X = x) \P(Y \in B) = g(x) \int_B h(y) \, dy = \int_B g(x) h(y) \, dy \] so again it follows that \( (X, Y) \) has PDF \( f \). The case where \( X \) has a continuous distribution on \( S \subseteq \R^j \) and \( Y \) has a discrete distribution on the countable set \( T \) is analogous.
The following result gives a converse to the last result. If the joint probability density factors into a function of \(x\) only and a function of \(y\) only, then \(X\) and \(Y\) are independent, and we can almost identify the individual probability density functions just from the factoring.
Factoring Theorem. Suppose that \((X, Y)\) has probability density function \(f\) of the form \[f(x, y) = u(x) v(y), \quad (x, y) \in S \times T\] where \(u: S \to [0, \infty)\) and \(v: T \to [0, \infty)\). Then \(X\) and \(Y\) are independent, and there exists a positve constant \(c\) such that \(X\) and \(Y\) have probability density functions \(g\) and \(h\), respectively, given by \begin{align} g(x) = & c \, u(x), \quad x \in S \\ h(y) = & \frac{1}{c} v(y), \quad y \in T \end{align}
Proof
Note that the proofs in the various cases are essentially the same, except for sums in the discrete case and integrals in the continuous case.
- Suppose that \( X \) and \( Y \) have discrete distributions on the countable sets \( S \) and \( T \), respectively, so that \( (X, Y) \) has a discrete distribution on \( S \times T \). In this case, the assumption is \[\P(X = x, Y = y) = u(x) v(y), \quad (x, y) \in S \times T\] Summing over \(y \in T\) in the displayed equation gives \(g(x) = \P(X = x) = c u(x)\) for \(x \in S\) where \(c = \sum_{y \in T} v(y)\). Similarly, summing over \(x \in S\) in the displayed equation gives \(h(y) = \P(Y = y) = k v(y)\) for \(y \in T\) where \(k = \sum_{x \in S} u(y)\). Summing over \((x, y) \in S \times T\) in the displayed equation gives \(1 = c k\) so \(k = 1 / c\). Finally, substituting gives \(\P(X = x, Y = y) = \P(X = x) \P(Y = y)\) for \((x, y) \in S \times T\) so \(X\) and \(Y\) are independent.
- Suppose next that \( X \) and \( Y \) have continuous distributions on \( S \subseteq \R^j \) and \( T \subseteq \R^k \) respectively. For \( A \subseteq S \) and \( B \subseteq T \), \[ \P(X \in A, Y \in B) = \P\left[(X, Y) \in A \times B\right] = \int_{A \times B} f(x, y) \, d(x, y) = \int_A u(x) \, dx \, \int_B v(y) dy \] Letting \( B = T \) in the displayed equation gives \( \P(X \in A) = \int_A c \, u(x) \, dx \) for \( A \subseteq S \), where \( c = \int_T v(y) \, dy \). By definition, \( X \) has PDF \( g = c \, u \). Next, letting \( A = S \) in the displayed equation gives \( \P(Y \in B) = \int_B k \, v(y) \, dy \) for \( B \subseteq T \), where \( k = \int_S u(x) \, dx \). Thus, \( Y \) has PDF \( g = k \, v \). Next, letting \( A = S \) and \( B = T \) in the displayed equation gives \( 1 = c \, k \), so \( k = 1 / c \). Now note that the displayed equation holds with \( u \) replaced by \( g \) and \( v \) replaced by \( h \), and this in turn gives \( \P(X \in A, Y \in B) = \P(X \in A) \P(Y \in B) \), so \( X \) and \( Y \) are independent.
- Suppose next that \( X \) has a discrete distribution on the countable set \( S \) and that \( Y \) has a continuous distributions on \( T \subseteq \R^k \). For \( x \in S \) and \( B \subseteq T \), \[ \P(X = x, Y \in B) = \int_B f(x, y) \, dy = u(x) \int_B v(y) \, dy \] Letting \( B = T \) in the displayed equation gives \( \P(X \in x) = c \, u(x) \) for \( x \in S \), where \( c = \int_T v(y) \, dy \). So \( X \) has PDF \( g = c \, u \). Next, summing over \( x \in S \) in the displayed equation gives \( \P(Y \in B) = k \int_B \, v(y) \, dy \) for \( B \subseteq T \), where \( k = \sum_{x \in S} u(x) \). Thus, \( Y \) has PDF \( g = k \, v \). Next, summing over \( x \in S \) and letting \( B = T \) in the displayed equation gives \( 1 = c \, k \), so \( k = 1 / c \). Now note that the displayed equation holds with \( u \) replaced by \( g \) and \( v \) replaced by \( h \), and this in turn gives \( \P(X = x, Y \in B) = \P(X = x) \P(Y \in B) \), so \( X \) and \( Y \) are independent. The case where where \( X \) has a continuous distribution on \( S \subseteq \R^j \) and \( Y \) has a discrete distribution on the countable set \( T \) is analogous.
The last two results extend to more than two random variables, because \(X\) and \(Y\) themselves may be random vectors. Here is the explicit statement:
Suppose that \(X_i\) is a random variable taking values in a set \(R_i\) with probability density funcion \(g_i\) for \(i \in \{1, 2, \ldots, n\}\), and that the random variables are independent. Then the random vector \(\bs X = (X_1, X_2, \ldots, X_n)\) taking values in \(S = R_1 \times R_2 \times \cdots \times R_n\) has probability density function \(f\) given by \[f(x_1, x_2, \ldots, x_n) = g_1(x_1) g_2(x_2) \cdots g_n(x_n), \quad (x_1, x_2, \ldots, x_n) \in S\]
The special case where the distributions are all the same is particularly important.
Suppose that \(\bs X = (X_1, X_2, \ldots, X_n)\) is a sequence of independent random variables, each taking values in a set \(R\) and with common probability density function \(g\). Then the probability density function \(f\) of \(\bs X\) on \(S = R^n\) is given by \[f(x_1, x_2, \ldots, x_n) = g(x_1) g(x_2) \cdots g(x_n), \quad (x_1, x_2, \ldots, x_n) \in S\]
In probability jargon, \(\bs X\) is a sequence of independent, identically distributed variables, a phrase that comes up so often that it is often abbreviated as IID. In statistical jargon, \(\bs X\) is a random sample of size \(n\) from the common distribution. As is evident from the special terminology, this situation is very impotant in both branches of mathematics. In statistics, the joint probability density function \(f\) plays an important role in procedures such as maximum likelihood and the identification of uniformly best estimators.
Recall that (mutual) independence of random variables is a very strong property. If a collection of random variables is independent, then any subcollection is also independent. New random variables formed from disjoint subcollections are independent. For a simple example, suppose that \(X\), \(Y\), and \(Z\) are independent real-valued random variables. Then
- \(\sin(X)\), \(\cos(Y)\), and \(e^Z\) are independent.
- \((X, Y)\) and \(Z\) are independent.
- \(X^2 + Y^2\) and \(\arctan(Z)\) are independent.
- \(X\) and \(Z\) are independent.
- \(Y\) and \(Z\) are independent.
In particular, note that statement 2 in the list above is much stronger than the conjunction of statements 4 and 5. Restated, if \(X\) and \(Z\) are dependent, then \((X, Y)\) and \(Z\) are also dependent.
Examples and Applications
Dice
Recall that a standard die is an ordinary six-sided die, with faces numbered from 1 to 6. The answers in the next couple of exercises give the joint distribution in the body of a table, with the marginal distributions literally in the magins. Such tables are the reason for the term marginal distibution.
Suppose that two standard, fair dice are rolled and the sequence of scores \((X_1, X_2)\) recorded. Our ususal assumption is that the variables \(X_1\) and \(X_2\) are independent. Let \(Y = X_1 + X_2\) and \(Z = X_1 - X_2\) denote the sum and difference of the scores, respectively.
- Find the probability density function of \((Y, Z)\).
- Find the probability density function of \(Y\).
- Find the probability density function of \(Z\).
- Are \(Y\) and \(Z\) independent?
Answer
Let \(f\) denote the PDF of \((Y, Z)\), \(g\) the PDF of \(Y\) and \(h\) the PDF of \(Z\). The PDFs are give in the following table. Random variables \(Y\) and \(Z\) are dependent
| \(f(y, z)\) | \(y = 2\) | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 11 | 12 | \(h(z)\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(z = -5\) | 0 | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) | 0 | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) |
| \(-4\) | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | 0 | 0 | 0 | \(\frac{2}{36}\) |
| \(-3\) | 0 | 0 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | 0 | 0 | \(\frac{3}{36}\) |
| \(-2\) | 0 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | 0 | \(\frac{4}{36}\) |
| \(-1\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{5}{36}\) |
| 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | \(\frac{6}{36}\) |
| 1 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{5}{36}\) |
| 2 | 0 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | 0 | \(\frac{4}{36}\) |
| 3 | 0 | 0 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | 0 | 0 | \(\frac{3}{36}\) |
| 4 | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | 0 | 0 | 0 | \(\frac{2}{36}\) |
| 5 | 0 | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) | 0 | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) |
| \(g(y)\) | \(\frac{1}{36}\) | \(\frac{2}{36}\) | \(\frac{3}{36}\) | \(\frac{4}{36}\) | \(\frac{5}{36}\) | \(\frac{6}{36}\) | \(\frac{5}{36}\) | \(\frac{4}{36}\) | \(\frac{3}{36}\) | \(\frac{2}{36}\) | \(\frac{1}{36}\) | 1 |
Suppose that two standard, fair dice are rolled and the sequence of scores \((X_1, X_2)\) recorded. Let \(U = \min\{X_1, X_2\}\) and \(V = \max\{X_1, X_2\}\) denote the minimum and maximum scores, respectively.
- Find the probability density function of \((U, V)\).
- Find the probability density function of \(U\).
- Find the probability density function of \(V\).
- Are \(U\) and \(V\) independent?
Answer
Let \(f\) denote the PDF of \((U, V)\), \(g\) the PDF of \(U\), and \(h\) the PDF of \(V\). The PDFs are given in the following table. Random variables \(U\) and \(V\) are dependent.
| \(f(u, v)\) | \(u = 1\) | 2 | 3 | 4 | 5 | 6 | \(h(v)\) |
|---|---|---|---|---|---|---|---|
| \(v = 1\) | \(\frac{1}{36}\) | 0 | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) |
| 2 | \(\frac{2}{36}\) | \(\frac{1}{36}\) | 0 | 0 | 0 | 0 | \(\frac{3}{36}\) |
| 3 | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{1}{36}\) | 0 | 0 | 0 | \(\frac{5}{36}\) |
| 4 | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{1}{36}\) | 0 | 0 | \(\frac{7}{36}\) |
| 5 | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{1}{36}\) | 0 | \(\frac{9}{36}\) |
| 6 | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{1}{36}\) | \(\frac{11}{36}\) |
| \(g(u)\) | \(\frac{11}{36}\) | \(\frac{9}{36}\) | \(\frac{7}{36}\) | \(\frac{5}{36}\) | \(\frac{3}{36}\) | \(\frac{1}{36}\) | 1 |
The previous two exercises show clearly how little information is given with the marginal distributions compared to the joint distribution. With the marginal PDFs alone, you could not even determine the support set of the joint distribution, let alone the values of the joint PDF.
Simple Continuous Distributions
Suppose that \((X, Y)\) has probability density function \(f\) given by \(f(x, y) = x + y\) for \(0 \le x \le 1\), \(0 \le y \le 1\).
- Find the probability density function of \(X\).
- Find the probability density function of \(Y\).
- Are \(X\) and \(Y\) independent?
Answer
- \(X\) has PDF \(g\) given by \(g(x) = x + \frac{1}{2}\) for \(0 \le x \le 1\)
- \(Y\) has PDF \(h\) given by \(h(y) = y + \frac{1}{2}\) for \(0 \le y \le 1\)
- \(X\) and \(Y\) are dependent.
Suppose that \((X, Y)\) has probability density function \(f\) given by \(f(x, y) = 2 ( x + y)\) for \(0 \le x \le y \le 1\).
- Find the probability density function of \(X\).
- Find the probability density function of \(Y\).
- Are \(X\) and \(Y\) independent?
Answer
- \(X\) has PDF \(g\) given by \(g(x) = (1 + 3 x)(1 - x)\) for \(0 \le x \le 1\).
- \(Y\) has PDF \(h\) given by \(h(h) = 3 y^2\) for \(0 \le y \le 1\).
- \(X\) and \(Y\) are dependent.
Suppose that \((X, Y)\) has probability density function \(f\) given by \(f(x, y) = 6 x^2 y\) for \(0 \le x \le 1\), \(0 \le y \le 1\).
- Find the probability density function of \(X\).
- Find the probability density function of \(Y\).
- Are \(X\) and \(Y\) independent?
Answer
- \(X\) has PDF \(g\) given by \(g(x) = 3 x^2\) for \(0 \le x \le 1\).
- \(Y\) has PDF \(h\) given by \(h(y) = 2 y\) for \(0 \le y \le 1\).
- \(X\) and \(Y\) are independent.
The last exercise is a good illustration of the factoring theorem. Without any work at all, we can tell that the PDF of \(X\) is proportional to \(x \mapsto x^2\) on the interval \([0, 1]\), the PDF of \(Y\) is proportional to \(y \mapsto y\) on the interval \([0, 1]\), and that \(X\) and \(Y\) are independent. The only thing unclear is how the constant 6 factors.
Suppose that \((X, Y)\) has probability density function \(f\) given by \(f(x, y) = 15 x^2 y\) for \(0 \le x \le y \le 1\).
- Find the probability density function of \(X\).
- Find the probability density function of \(Y\).
- Are \(X\) and \(Y\) independent?
Answer
- \(X\) has PDF \(g\) given by \(g(x) = \frac{15}{2} x^2 \left(1 - x^2\right)\) for \(0 \le x \le 1\).
- \(Y\) has PDF \(h\) given by \(h(y) = 5 y^4\) for \(0 \le y \le 1\).
- \(X\) and \(Y\) are dependent.
Note that in the last exercise, the factoring theorem does not apply. Random variables \(X\) and \(Y\) each take values in \([0, 1]\), but the joint PDF factors only on part of \([0, 1]^2\).
Suppose that \((X, Y, Z)\) has probability density function \(f\) given \(f(x, y, x) = 2 (x + y) z\) for \(0 \le x \le 1\), \(0 \le y \le 1\), \(0 \le z \le 1\).
- Find the probability density function of each pair of variables.
- Find the probability density function of each variable.
- Determine the dependency relationships between the variables.
Proof
- \((X, Y)\) has PDF \(f_{1,2}\) given by \(f_{1,2}(x,y) = x + y\) for \(0 \le x \le 1\), \(0 \le y \le 1\).
- \((X, Z)\) has PDF \(f_{1,3}\) given by \(f_{1,3}(x,z) = 2 z \left(x + \frac{1}{2}\right)\) for \(0 \le x \le 1\), \(0 \le z \le 1\).
- \((Y, Z)\) had PDF \(f_{2,3}\) given by \(f_{2,3}(y,z) = 2 z \left(y + \frac{1}{2}\right)\) for \(0 \le y \le 1\), \(0 \le z \le 1\).
- \(X\) has PDF \(f_1\) given by \(f_1(x) = x + \frac{1}{2}\) for \(0 \le x \le 1\).
- \(Y\) has PDF \(f_2\) given by \(f_2(y) = y + \frac{1}{2}\) for \(0 \le y \le 1\).
- \(Z\) has PDF \(f_3\) given by \(f_3(z) = 2 z\) for \(0 \le z \le 1\).
- \(Z\) and \((X, Y)\) are independent; \(X\) and \(Y\) are dependent.
Suppose that \((X, Y)\) has probability density function \(f\) given by \(f(x, y) = 2 e^{-x} e^{-y}\) for \(0 \le x \le y \lt \infty\).
- Find the probability density function of \(X\).
- Find the probability density function of \(Y\).
- Are \(X\) and \(Y\) independent?
Answer
- \(X\) has PDF \(g\) given by \(g(x) = 2 e^{-2 x}\) for \(0 \le x \lt \infty\).
- \(Y\) has PDF \(h\) given by \(h(y) = 2 \left(e^{-y} - e^{-2y}\right)\) for \(0 \le y \lt \infty\).
- \(X\) and \(Y\) are dependent.
In the previous exercise, \( X \) has an exponential distribution with rate parameter 2. Recall that exponential distributions are widely used to model random times, particularly in the context of the Poisson model.
Suppose that \(X\) and \(Y\) are independent, and that \(X\) has probability density function \(g\) given by \(g(x) = 6 x (1 - x)\) for \(0 \le x \le 1\), and that \(Y\) has probability density function \(h\) given by \(h(y) = 12 y^2 (1 - y)\) for \(0 \le y \le 1\).
- Find the probability density function of \((X, Y)\).
- Find \(\P(X + Y \le 1)\).
Answer
- \((X, Y)\) has PDF \(f\) given by \(f(x, y) = 72 x (1 - x) y^2 (1 - y)\) for \(0 \le x \le 1\), \(0 \le y \le 1\).
- \(\P(X + Y \le 1) = \frac{13}{35}\)
In the previous exercise, \( X \) and \( Y \) have beta distributions, which are widely used to model random probabilities and proportions. Beta distributions are studied in more detail in the chapter on Special Distributions.
Suppose that \(\Theta\) and \(\Phi\) are independent random angles, with common probability density function \(g\) given by \(g(t) = \sin(t)\) for \(0 \le t \le \frac{\pi}{2}\).
- Find the probability density function of \((\Theta, \Phi)\).
- Find \(\P(\Theta \le \Phi)\).
Answer
- \((\Theta, \Phi)\) has PDF \(f\) given by \(f(\theta, \phi) = \sin(\theta) \sin(\phi)\) for \(0 \le \theta \le \frac{\pi}{2}\), \(0 \le \phi \le \frac{\pi}{2}\).
- \(\P(\Theta \le \Phi) = \frac{1}{2}\)
The common distribution of \( X \) and \( Y \) in the previous exercise governs a random angle in Bertrand's problem.
Suppose that \(X\) and \(Y\) are independent, and that \(X\) has probability density function \(g\) given by \(g(x) = \frac{2}{x^3}\) for \(1 \le x \lt \infty\), and that \(Y\) has probability density function \(h\) given by \(h(y) = \frac{3}{y^4}\) for \(1 \le y \lt\infty\).
- Find the probability density function of \((X, Y)\).
- Find \(\P(X \le Y)\).
Answer
- \((X, Y)\) has PDF \(f\) given by \(f(x, y) = \frac{6}{x^3 y^4}\) for \(1 \le x \lt \infty\), \(1 \le y \lt \infty\).
- \(\P(X \le Y) = \frac{2}{5}\)
Both \(X\) and \(Y\) in the previous exercise have Pareto distributions, named for Vilfredo Pareto. Recall that Pareto distributions are used to model certain economic variables and are studied in more detail in the chapter on Special Distributions.
Suppose that \((X, Y)\) has probability density function \(g\) given by \(g(x, y) = 15 x^2 y\) for \(0 \le x \le y \le 1\), and that \(Z\) has probability density function \(h\) given by \(h(z) = 4 z^3\) for \(0 \le z \le 1\), and that \((X, Y)\) and \(Z\) are independent.
- Find the probability density function of \((X, Y, Z)\).
- Find the probability density function of \((X, Z)\).
- Find the probability density function of \((Y, Z)\).
- Find \(\P(Z \le X Y)\).
Answer
- \((X, Y, Z)\) has PDF \(f\) given by \(f(x, y, z) = 60 x^2 y z^3\) for \(0 \le x \le y \le 1\), \(0 \le z \le 1\).
- \((X, Z)\) has PDF \(f_{1,3}\) given by \(f_{1,3}(x, z) = 30 x^2 \left(1 - x^2\right) z^3\) for \(0 \le x \le 1\), \(0 \le z \le 1\).
- \((Y, Z)\) has PDF \(f_{2,3}\) given by \(f_{2,3}(y, z) = 20 y^4 z^3\) for \(0 \le y \le 1\), \(0 \le z \le 1\).
- \(\P(Z \le X Y) = \frac{15}{92}\)
Multivariate Uniform Distributions
Multivariate uniform distributions give a geometric interpretation of some of the concepts in this section.
Recall first that for \( n \in \N_+ \), the standard measure on \(\R^n\) is \[\lambda_n(A) = \int_A 1 dx, \quad A \subseteq \R^n\] In particular, \(\lambda_1(A)\) is the length of \(A \subseteq \R\), \(\lambda_2(A)\) is the area of \(A \subseteq \R^2\), and \(\lambda_3(A)\) is the volume of \(A \subseteq \R^3\).
Details
Technically \(\lambda_n\) is Lebesgue measure on the measurable subsets of \(\R^n\). The integral representation is valid for the types of sets that occur in applications. In the discussion below, all subsets are assumed to be measurable.
Suppose now that \(X\) takes values in \(\R^j\), \(Y\) takes values in \(\R^k\), and that \((X, Y)\) is uniformly distributed on a set \(R \subseteq \R^{j+k}\). So \(0 \lt \lambda_{j+k}(R) \lt \infty \) and the joint probability density function \( f \) of \((X, Y)\) is given by \( f(x, y) = 1 \big/ \lambda_{j+k}(R) \) for \( (x, y) \in R \). Recall that uniform distributions always have constant density functions. Now let \(S\) and \(T\) be the projections of \(R\) onto \(\R^j\) and \(\R^k\) respectively, defined as follows: \[ S = \left\{x \in \R^j: (x, y) \in R \text{ for some } y \in \R^k\right\}, \; T = \left\{y \in \R^k: (x, y) \in R \text{ for some } x \in \R^j\right\}\] Note that \(R \subseteq S \times T\). Next we denote the cross sections at \(x \in S\) and at \(y \in T\), respectively by \[T_x = \{t \in T: (x, t) \in R\}, \; S_y = \{s \in S: (s, y) \in R\}\]
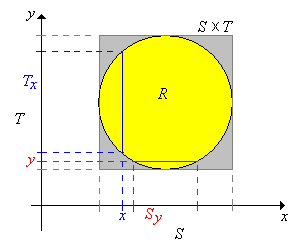
\(X\) takes values in \(S\) and \( Y \) takes values in \( T \). The probability density functions \(g\) and \( h \) of \(X\) and \( Y \) are proportional to the cross-sectional measures:
- \( g(x) = \lambda_k\left(T_x\right) \big/ \lambda_{j+k}(R) \) for \( x \in S \)
- \( h(y) = \lambda_j\left(S_y\right) \big/ \lambda_{j+k}(R) \) for \( y \in T \)
Proof
From our general theory, \( X \) has PDF \( g \) given by \[ g(x) = \int_{T_x} f(x, y) \, dy = \int_{T_x} \frac{1}{\lambda_{j+k}(R)} \, dy = \frac{\lambda_k\left(T_x\right)}{\lambda_{j+k}(R)}, \quad x \in S \] Technically, it's possible that \(\lambda_k(T_x) = \infty\) for some \(x \in S\), but the set of such \(x\) has measure 0. That is, \(\lambda_j\{x \in S: \lambda_k(T_x) = \infty\} = 0\). The result for \( Y \) is analogous.
In particular, note from previous theorem that \(X\) and \(Y\) are neither independent nor uniformly distributed in general. However, these properties do hold if \(R\) is a Cartesian product set.
Suppose that \(R = S \times T\).
- \(X\) is uniformly distributed on \(S\).
- \(Y\) is uniformly distributed on \(T\).
- \(X\) and \(Y\) are independent.
Proof
In this case, \( T_x = T \) and \( S_y = S \) for every \( x \in S \) and \( y \in T \). Also, \( \lambda_{j+k}(R) = \lambda_j(S) \lambda_k(T) \), so for \( x \in S \) and \( y \in T \), \( f(x, y) = 1 \big/ [\lambda_j(S) \lambda_k(T)] \), \( g(x) = 1 \big/ \lambda_j(S) \), \( h(y) = 1 \big/ \lambda_k(T) \).
In each of the following cases, find the joint and marginal probabilit density functions, and determine if \(X\) and \(Y\) are independent.
- \((X, Y)\) is uniformly distributed on the square \(R = [-6, 6]^2\).
- \((X, Y)\) is uniformly distributed on the triangle \(R = \{(x, y): -6 \le y \le x \le 6\}\).
- \((X, Y)\) is uniformly distributed on the circle \(R = \left\{(x, y): x^2 + y^2 \le 36\right\}\).
Answer
In the following, \(f\) is the PDF of \((X, Y)\), \(g\) the PDF of \(X\), and \(h\) the PDF of \(Y\).
-
- \(f(x, y) = \frac{1}{144}\) for \(-6 \le x \le 6\), \(-6 \le y \le 6\)
- \(g(x) = \frac{1}{12}\) for \(-6 \le x \le 6\)
- \(h(y) = \frac{1}{12}\) for \(-6 \le y \le 6\)
- \(X\) and \(Y\) are independent.
-
- \(f(x, y) = \frac{1}{72}\) for \(-6 \le y \le x \le 6\)
- \(g(x) = \frac{1}{72}(x + 6)\) for \(-6 \le x \le 6\)
- \(h(y) = \frac{1}{72}(y + 6)\) for \(-6 \le y \le 6\)
- \(X\) and \(Y\) are dependent.
-
- \(f(x, y) = \frac{1}{36 \pi}\) for \(x^2 + y^2 \le 36\)
- \(g(x) = \frac{1}{18 \pi} \sqrt{36 - x^2}\) for \(-6 \le x \le 6\)
- \(h(y) = \frac{1}{18 \pi} \sqrt{36 - y^2}\) for \(-6 \le y \le 6\)
- \(X\) and \(Y\) are dependent.
In the bivariate uniform experiment, run the simulation 1000 times for each of the following cases. Watch the points in the scatter plot and the graphs of the marginal distributions. Interpret what you see in the context of the discussion above.
- square
- triangle
- circle
Suppose that \((X, Y, Z)\) is uniformly distributed on the cube \([0, 1]^3\).
- Give the joint probability density function of \((X, Y, Z)\).
- Find the probability density function of each pair of variables.
- Find the probability density function of each variable
- Determine the dependency relationships between the variables.
Answer
- \((X, Y, Z)\) has PDF \(f\) given by \(f(x, y, z) = 1\) for \(0 \le x \le 1\), \(0 \le y \le 1\), \(0 \le z \le 1\) (the uniform distribution on \([0, 1]^3\))
- \((X, Y)\), \((X, Z)\), and \((Y, Z)\) have common PDF \(g\) given by \(g(u, v) = 1\) for \(0 \le u \le 1\), \(0 \le v \le 1\) (the uniform distribution on \([0, 1]^2\))
- \(X\), \(Y\), and \(Z\) have common PDF \(h\) given by \(h(u) = 1\) for \(0 \le u \le 1\) (the uniform distribution on \([0, 1]\))
- \(X\), \(Y\), \(Z\) are independent.
Suppose that \((X, Y, Z)\) is uniformly distributed on \(\{(x, y, z): 0 \le x \le y \le z \le 1\}\).
- Give the joint density function of \((X, Y, Z)\).
- Find the probability density function of each pair of variables.
- Find the probability density function of each variable
- Determine the dependency relationships between the variables.
Answer
- \((X, Y, Z)\) has PDF \(f\) given by \(f(x, y, z) = 6\) for \(0 \le x \le y \le z \le 1\)
-
- \((X, Y)\) has PDF \(f_{1,2}\) given by \(f_{1,2}(x, y) = 6 (1 - y)\) for \(0 \le x \le y \le 1\)
- \((X, Z)\) has PDF \(f_{1,3}\) given by \(f_{1,3}(x, z) = 6 (z - x)\) for \(0 \le x \le z \le 1\)
- \((Y, Z)\) has PDF \(f_{2,3}\) given by \(f_{2,3}(y, z) = 6 y\) for \(0 \le y \le z \le 1\)
-
- \(X\) has PDF \(f_1\) given by \(f_1(x) = 3 (1 - x)^2\) for \(0 \le x \le 1\)
- \(Y\) has PDF \(f_2\) given by \(f_2(y) = 6 y (1 - y)\) for \(0 \le y \le 1\)
- \(Z\) has PDF \(f_3\) given by \(f_3(z) = 3 z^2\) for \(0 \le z \le 1\)
- Each pair of variables is dependent.
The Rejection Method
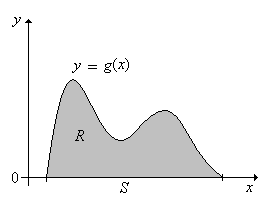
The following result shows how an arbitrary continuous distribution can be obtained from a uniform distribution. This result is useful for simulating certain continuous distributions, as we will see. To set up the basic notation, suppose that \(g\) is a probability density function for a continuous distribution on \(S \subseteq \R^n\). Let \[R = \{(x, y): x \in S \text{ and } 0 \le y \le g(x)\} \subseteq \R^{n+1} \]
If \((X, Y)\) is uniformly distributed on \(R\), then \(X\) has probability density function \(g\).
Proof
Note that since \(g\) is a probability density function on \(S\). \[ \lambda_{n+1}(R) = \int_R 1 \, d(x, y) = \int_S \int_0^{g(x)} 1 \, dy \, dx = \int_S g(x) \, dx = 1 \] Hence the probability density function \( f \) of \((X, Y)\) is given by \(f(x, y) = 1\) for \((x, y) \in R\). Thus, the probability density function of \(X\) is \(x \mapsto \int_0^{g(x)} 1 \, dy = g(x)\) for \( x \in S \).
A picture in the case \(n = 1\) is given below:
The next result gives the rejection method for simulating a random variable with the probability density function \(g\).
Suppose now that \( R \subseteq T \) where \( T \subseteq \R_{n+1} \) with \( \lambda_{n+1}(T) \lt \infty \) and that \(\left((X_1, Y_1), (X_2, Y_2), \ldots\right)\) is a sequence of independent random variables with \( X_k \in \R^n \), \( Y_k \in \R \), and \( \left(X_k, Y_k\right) \) uniformly distributed on \( T \) for each \( k \in \N_+ \). Let \[N = \min\left\{k \in \N_+: \left(X_k, Y_k\right) \in R\right\} = \min\left\{k \in \N_+: X_k \in S, \; 0 \le Y_k \le g\left(X_k\right)\right\}\]
- \( N \) has the geometric distribution on \(\N_+\) with success parameter \( p = 1 / \lambda_{n+1}(T) \).
- \(\left(X_N, Y_N\right)\) is uniformly distributed on \(R\).
- \(X_N\) has probability density function \(g\).
Proof
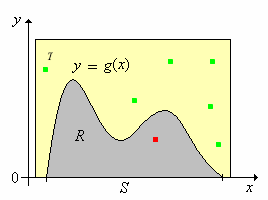
The point of the theorem is that if we can simulate a sequence of independent variables that are uniformly distributed on \( T \), then we can simulate a random variable with the given probability density function \( g \). Suppose in particular that \( R \) is bounded as a subset of \( \R^{n+1} \), which would mean that the domain \( S \) is bounded as a subset of \( \R^n \) and that the probability density function \( g \) is bounded on \( S \). In this case, we can find \( T \) that is the Cartesian product of \( n + 1 \) bounded intervals with \( R \subseteq T \). It turns out to be very easy to simulate a sequence of independent variables, each uniformly distributed on such a product set, so the rejection method always works in this case. As you might guess, the rejection method works best if the size of \( T \), namely \( \lambda_{n+1}(T) \), is small, so that the success parameter \( p \) is large.
The rejection method app simulates a number of continuous distributions via the rejection method. For each of the following distributions, vary the parameters and note the shape and location of the probability density function. Then run the experiment 1000 times and observe the results.
- The beta distribution
- The semicircle distribution
- The triangle distribution
- The U-power distribution
The Multivariate Hypergeometric Distribution
Suppose that a population consists of \(m\) objects, and that each object is one of four types. There are \(a\) type 1 objects, \(b\) type 2 objects, \(c\) type 3 objects and \(m - a - b - c\) type 0 objects. We sample \(n\) objects from the population at random, and without replacement. The parameters \(m\), \(a\), \(b\), \(c\), and \(n\) are nonnegative integers with \(a + b + c \le m\) and \(n \le m\). Denote the number of type 1, 2, and 3 objects in the sample by \(X\), \(Y\), and \(Z\), respectively. Hence, the number of type 0 objects in the sample is \(n - X - Y - Z\). In the problems below, the variables \(x\), \(y\), and \(z\) take values in \(\N\).
\((X, Y, Z)\) has a (multivariate) hypergeometric distribution with probability density function \(f\) given by \[f(x, y, z) = \frac{\binom{a}{x} \binom{b}{y} \binom{c}{z} \binom{m - a - b - c}{n - x - y - z}}{\binom{m}{n}}, \quad x + y + z \le n\]
Proof
From the basic theory of combinatorics, the numerator is the number of ways to select an unordered sample of size \( n \) from the population with \( x \) objects of type 1, \( y \) objects of type 2, \( z \) objects of type 3, and \( n - x - y - z \) objects of type 0. The denominator is the total number of ways to select the unordered sample.
\((X, Y)\) also has a (multivariate) hypergeometric distribution, with the probability density function \(g\) given by \[g(x, y) = \frac{\binom{a}{x} \binom{b}{y} \binom{m - a - b}{n - x - y}}{\binom{m}{n}}, \quad x + y \le n\]
Proof
This result could be obtained by summing the joint PDF over \( z \) for fixed \( (x, y) \). However, there is a much nicer combinatorial argument. Note that we are selecting a random sample of size \(n\) from a population of \(m\) objects, with \(a\) objects of type 1, \(b\) objects of type 2, and \(m - a - b\) objects of other types.
\(X\) has an ordinary hypergeometric distribution, with probability density function \(h\) given by \[h(x) = \frac{\binom{a}{x} \binom{m - a}{n - x}}{\binom{m}{n}}, \quad x \le n\]
Proof
Again, the result could be obtained by summing the joint PDF for \( (X, Y, Z) \) over \( (y, z) \) for fixed \( x \), or by summing the joint PDF for \( (X, Y) \) over \( y \) for fixed \( x \). But as before, there is a much more elegant combinatorial argument. Note that we are selecting a random sample of size \(n\) from a population of size \(m\) objects, with \(a\) objects of type 1 and \(m - a\) objects of other types.
These results generalize in a straightforward way to a population with any number of types. In brief, if a random vector has a hypergeometric distribution, then any sub-vector also has a hypergeometric distribution. In other words, all of the marginal distributions of a hypergeometric distribution are themselves hypergeometric. Note however, that it's not a good idea to memorize the formulas above explicitly. It's better to just note the patterns and recall the combinatorial meaning of the binomial coefficient. The hypergeometric distribution and the multivariate hypergeometric distribution are studied in more detail in the chapter on Finite Sampling Models.
Suppose that a population of voters consists of 50 democrats, 40 republicans, and 30 independents. A sample of 10 voters is chosen at random from the population (without replacement, of course). Let \(X\) denote the number of democrats in the sample and \(Y\) the number of republicans in the sample. Find the probability density function of each of the following:
- \((X, Y)\)
- \(X\)
- \(Y\)
Answer
In the formulas for the PDFs below, the variables \(x\) and \(y\) are nonnegative integers.
- \((X, Y)\) has PDF \(f\) given by \(f(x, y) = \frac{1}{\binom{120}{10}} \binom{50}{x} \binom{40}{y} \binom{30}{10 - x - y}\) for \(x + y \le 10\)
- \(X\) has PDF \(g\) given by \(g(x) = \frac{1}{\binom{120}{10}} \binom{50}{x} \binom{70}{10 - x}\) for \(x \le 10\)
- \(Y\) has PDF \(h\) given by \(h(y) = \frac{1}{\binom{120}{10}} \binom{40}{y} \binom{80}{10 - y}\) for \(y \le 10\)
Suppose that the Math Club at Enormous State University (ESU) has 50 freshmen, 40 sophomores, 30 juniors and 20 seniors. A sample of 10 club members is chosen at random to serve on the \(\pi\)-day committee. Let \(X\) denote the number freshmen on the committee, \(Y\) the number of sophomores, and \(Z\) the number of juniors.
- Find the probability density function of \((X, Y, Z)\)
- Find the probability density function of each pair of variables.
- Find the probability density function of each individual variable.
Answer
In the formulas for the PDFs below, the variables \(x\), \(y\), and \(z\) are nonnegative integers.
- \((X, Y, Z)\) has PDF \(f\) given by \(f(x, y, z) = \frac{1}{\binom{140}{10}} \binom{50}{x} \binom{40}{y} \binom{30}{z} \binom{20}{10 - x - y - z}\) for \(x + y + z \le 10\).
-
- \((X, Y)\) has PDF \(f_{1,2}\) given by \(f_{1,2}(x, y) = \frac{1}{\binom{140}{10}} \binom{50}{x} \binom{40}{y} \binom{50}{10 - x - y}\) for \(x + y \le 10\).
- \((X, Z)\) has PDF \(f_{1,3}\) given by \(f_{1,3}(y, z) = \frac{1}{\binom{140}{10}} \binom{50}{x} \binom{30}{z} \binom{60}{10 - x - z}\) for \(x + z \le 10\).
- \((Y, Z)\) has PDF \(f_{2,3}\) given by \(f_{2,3}(y, z) = \frac{1}{\binom{140}{10}} \binom{40}{y} \binom{30}{z} \binom{70}{10 - y - z}\) for \(y + z \le 10\).
-
- \(X\) has PDF \(f_1\) given by \(f_1(x) = \frac{1}{\binom{120}{10}} \binom{50}{x} \binom{90}{10 - x}\) for \(x \le 10\).
- \(Y\) has PDF \(f_2\) given by \(f_2(y) = \frac{1}{\binom{120}{10}} \binom{40}{y} \binom{100}{10 - y}\) for \(y \le 10\).
- \(Z\) has PDF \(f_3\) given by \(f_3(z) = \frac{1}{\binom{120}{10}} \binom{30}{z} \binom{110}{10 - z}\) for \(z \le 10\)
Multinomial Trials
Suppose that we have a sequence of \(n\) independent trials, each with 4 possible outcomes. On each trial, outcome 1 occurs with probability \(p\), outcome 2 with probability \(q\), outcome 3 with probability \(r\), and outcome 0 occurs with probability \(1 - p - q - r\). The parameters \(p\), \(q\), and \(r\) are nonnegative numbers with \(p + q + r \le 1\), and \(n \in \N_+\). Denote the number of times that outcome 1, outcome 2, and outcome 3 occurred in the \(n\) trials by \(X\), \(Y\), and \(Z\) respectively. Of course, the number of times that outcome 0 occurs is \(n - X - Y - Z\). In the problems below, the variables \(x\), \(y\), and \(z\) take values in \(\N\).
\((X, Y, Z)\) has a multinomial distribution with probability density function \(f\) given by \[f(x, y, z) = \binom{n}{x, \, y, \, z} p^x q^y r^z (1 - p - q - r)^{n - x - y - z}, \quad x + y + z \le n\]
Proof
The multinomial coefficient is the number of sequences of length \( n \) with 1 occurring \( x \) times, 2 occurring \( y \) times, 3 occurring \( z \) times, and 0 occurring \( n - x - y - z \) times. The result then follows by independence.
\((X, Y)\) also has a multinomial distribution with the probability density function \(g\) given by \[g(x, y) = \binom{n}{x, \, y} p^x q^y (1 - p - q)^{n - x - y}, \quad x + y \le n\]
Proof
This result could be obtained from the joint PDF above, by summing over \( z \) for fixed \( (x, y) \). However there is a much better direct argument. Note that we have \(n\) independent trials, and on each trial, outcome 1 occurs with probability \(p\), outcome 2 with probability \(q\), and some other outcome with probability \(1 - p - q\).
\(X\) has a binomial distribution, with the probability density function \(h\) given by \[h(x) = \binom{n}{x} p^x (1 - p)^{n - x}, \quad x \le n\]
Proof
Again, the result could be obtained by summing the joint PDF for \( (X, Y, Z) \) over \( (y, z) \) for fixed \( x \) or by summing the joint PDF for \( (X, Y) \) over \( y \) for fixed \( x \). But as before, there is a much better direct argument. Note that we have \(n\) independent trials, and on each trial, outcome 1 occurs with probability \(p\) and some other outcome with probability \(1 - p\).
These results generalize in a completely straightforward way to multinomial trials with any number of trial outcomes. In brief, if a random vector has a multinomial distribution, then any sub-vector also has a multinomial distribution. In other terms, all of the marginal distributions of a multinomial distribution are themselves multinomial. The binomial distribution and the multinomial distribution are studied in more detail in the chapter on Bernoulli Trials.
Suppose that a system consists of 10 components that operate independently. Each component is working with probability \(\frac{1}{2}\), idle with probability \(\frac{1}{3}\), or failed with probability \(\frac{1}{6}\). Let \(X\) denote the number of working components and \(Y\) the number of idle components. Give the probability density function of each of the following:
- \((X, Y)\)
- \(X\)
- \(Y\)
Answer
In the formulas below, the variables \(x\) and \(y\) are nonnegative integers.
- \((X, Y)\) has PDF \(f\) given by \(f(x, y) = \binom{10}{x, \; y} \left(\frac{1}{2}\right)^x \left(\frac{1}{3}\right)^y \left(\frac{1}{6}\right)^{10 - x - y}\) for \(x + y \le 10\).
- \(X\) has PDF \(g\) given by \(g(x) = \binom{10}{x} \left(\frac{1}{2}\right)^{10}\) for \(x \le 10\).
- \(Y\) has PDF \(h\) given by \(h(y) = \binom{10}{y} \left(\frac{1}{3}\right)^y \left(\frac{2}{3}\right)^{10 - y}\) for \(y \le 10\).
Suppose that in a crooked, four-sided die, face \(i\) occurs with probability \(\frac{i}{10}\) for \(i \in \{1, 2, 3, 4\}\). The die is thrown 12 times; let \(X\) denote the number of times that score 1 occurs, \(Y\) the number of times that score 2 occurs, and \(Z\) the number of times that score 3 occurs.
- Find the probability density function of \((X, Y, Z)\)
- Find the probability density function of each pair of variables.
- Find the probability density function of each individual variable.
Answer
In the formulas for the PDFs below, the variables \(x\), \(y\) and \(z\) are nonnegative integers.
- \((X, Y, Z)\) has PDF \(f given by \(f(x, y, z) = \binom{12}{x, \, y, \, z} \left(\frac{1}{10}\right)^x \left(\frac{2}{10}\right)^y \left(\frac{3}{10}\right)^z \left(\frac{4}{10}\right)^{12 - x - y - z}\), \(x + y + z \le 12\)
-
- \((X, Y)\) has PDF \(f_{1,2}\) given by \(f_{1,2}(x, y) = \binom{12}{x, \; y} \left(\frac{1}{10}\right)^{x} \left(\frac{2}{10}\right)^y \left(\frac{7}{10}\right)^{12 - x - y}\) for \(x + y \le 12\).
- \((X, Z)\) has PDF \(f_{1,3}\) given by \(f_{1,3}(x, z) = \binom{12}{x, \; z} \left(\frac{1}{10}\right)^{x} \left(\frac{3}{10}\right)^z \left(\frac{6}{10}\right)^{12 - x - z}\) for \(x + z \le 12\).
- \((Y, Z)\) has PDF \(f_{2,3}\) given by \(f_{2,3}(y, z) = \binom{12}{y, \; z} \left(\frac{2}{10}\right)^{y} \left(\frac{3}{10}\right)^z \left(\frac{5}{10}\right)^{12 - y - z}\) for \(y + z \le 12\).
-
- \(X\) has PDF \(f_1\) given by \(f_1(x) = \binom{12}{x} \left(\frac{1}{10}\right)^x \left(\frac{9}{10}\right)^{12 - x}\) for \(x \le 12\).
- \(Y\) has PDF \(f_2\) given by \(f_2(y) = \binom{12}{y} \left(\frac{2}{10}\right)^y \left(\frac{8}{10}\right)^{12 - y}\) for \(y \le 12\).
- \(Z\) has PDF \(f_3\) given by \(f_3(z) = \binom{12}{z} \left(\frac{3}{10}\right)^z \left(\frac{7}{10}\right)^{12 - z}\) for \(z \le 12\).
Bivariate Normal Distributions
Suppose that \((X, Y)\) has probability the density function \(f\) given below: \[f(x, y) = \frac{1}{12 \pi} \exp\left[-\left(\frac{x^2}{8} + \frac{y^2}{18}\right)\right], \quad (x, y) \in \R^2\]
- Find the probability density function of \(X\).
- Find the probability density function of \(Y\).
- Are \(X\) and \(Y\) independent?
Answer
- \(X\) has PDF \(g\) given by \(g(x) = \frac{1}{2 \sqrt{2 \pi}} e^{-x^2 / 8}\) for \(x \in \R\).
- \(Y\) has PDF \(h\) given by \(h(y) = \frac{1}{3 \sqrt{2 \pi}} e^{-y^2 /18}\) for \(y \in \R\).
- \(X\) and \(Y\) are independent.
Suppose that \((X, Y)\) has probability density function \(f\) given below:
\[f(x, y) = \frac{1}{\sqrt{3} \pi} \exp\left[-\frac{2}{3}\left(x^2 - x y + y^2\right)\right], \quad(x, y) \in \R^2\]- Find the density function of \(X\).
- Find the density function of \(Y\).
- Are \(X\) and \(Y\) independent?
Answer
- \(X\) has PDF \(g\) given by \(g(x) = \frac{1}{\sqrt{2 \pi}} e^{-x^2 / 2}\) for \(x \in \R\).
- \(Y\) has PDF \(h\) given by \(h(y) = \frac{1}{\sqrt{2 \pi}} e^{-y^2 / 2}\) for \(y \in \R\).
- \(X\) and \(Y\) are dependent.
The joint distributions in the last two exercises are examples of bivariate normal distributions. Normal distributions are widely used to model physical measurements subject to small, random errors. In both exercises, the marginal distributions of \( X \) and \( Y \) also have normal distributions, and this turns out to be true in general. The multivariate normal distribution is studied in more detail in the chapter on Special Distributions.
Exponential Distributions
Recall that the exponential distribution has probability density function \[f(x) = r e^{-r t}, \quad x \in [0, \infty)\] where \(r \in (0, \infty)\) is the rate parameter. The exponential distribution is widely used to model random times, and is studied in more detail in the chapter on the Poisson Process.
Suppose \(X\) and \(Y\) have exponential distributions with parameters \(a \in (0, \infty)\) and \(b \in (0, \infty)\), respectively, and are independent. Then \(\P(X \lt Y) = \frac{a}{a + b}\).
Suppose \(X\), \(Y\), and \(Z\) have exponential distributions with parameters \(a \in (0, \infty)\), \(b \in (0, \infty)\), and \(c \in (0, \infty)\), respectively, and are independent. Then
- \(\P(X \lt Y \lt Z) = \frac{a}{a + b + c} \frac{b}{b + c}\)
- \(\P(X \lt Y, X \lt Z) = \frac{a}{a + b + c}\)
If \(X\), \(Y\), and \(Z\) are the lifetimes of devices that act independently, then the results in the previous two exercises give probabilities of various failure orders. Results of this type are also very important in the study of continuous-time Markov processes. We will continue this discussion in the section on transformations of random variables.
Mixed Coordinates
Suppose \(X\) takes values in the finite set \(\{1, 2, 3\}\), \(Y\) takes values in the interval \([0, 3]\), and that \((X, Y)\) has probability density function \(f\) given by \[f(x, y) = \begin{cases} \frac{1}{3}, & \quad x = 1, \; 0 \le y \le 1 \\ \frac{1}{6}, & \quad x = 2, \; 0 \le y \le 2 \\ \frac{1}{9}, & \quad x = 3, \; 0 \le y \le 3 \end{cases}\]
- Find the probability density function of \(X\).
- Find the probability density function of \(Y\).
- Are \(X\) and \(Y\) independent?
Answer
- \(X\) has PDF \(g\) given by \(g(x) = \frac{1}{3}\) for \(x \in \{1, 2, 3\}\) (the uniform distribution on \(\{1, 2, 3\}\)).
- \(Y\) has PDF \(h\) given by \(h(y) = \begin{cases} \frac{11}{18}, & 0 \lt y \lt 1 \\ \frac{5}{18}, & 1 \lt y \lt 2 \\ \frac{2}{18}, & 2 \lt y \lt 3 \end{cases}\).
- \(X\) and \(Y\) are dependent.
Suppose that \(P\) takes values in the interval \([0, 1]\), \(X\) takes values in the finite set \(\{0, 1, 2, 3\}\), and that \((P, X)\) has probability density function \(f\) given by \[f(p, x) = 6 \binom{3}{x} p^{x + 1} (1 - p)^{4 - x}, \quad (p, x) \in [0, 1] \times \{0, 1, 2, 3\}\]
- Find the probability density function of \(P\).
- Find the probability density function of \(X\).
- Are \(P\) and \(X\) independent?
Answer
- \(P\) has PDF \(g\) given by \(g(p) = 6 p (1 - p)\) for \(0 \le p \le 1\).
- \(X\) has PDF \(h\) given by \( h(0) = h(3) = \frac{1}{5} \), \( h(1) = \frac{3}{10} \)
- \(P\) and \(X\) are dependent.
As we will see in the section on conditional distributions, the distribution in the last exercise models the following experiment: a random probability \(P\) is selected, and then a coin with this probability of heads is tossed 3 times; \(X\) is the number of heads. Note that \( P \) has a beta distribution.
Random Samples
Recall that the Bernoulli distribution with parameter \(p \in [0, 1]\) has probability density function \(g\) given by \(g(x) = p^x (1 - p)^{1 - x}\) for \(x \in \{0, 1\}\). Let \(\bs X = (X_1, X_2, \ldots, X_n)\) be a random sample of size \(n \in \N_+\) from the distribution. Give the probability density funcion of \(\bs X\) in simplified form.
Answer
\(\bs X\) has PDF \(f\) given by \(f(x_1, x_2, \ldots, x_n) = p^y (1 - p)^{n-y}\) for \((x_1, x_2, \ldots, x_n) \in \{0, 1\}^n\), where \(y = x_1 + x_2 + \cdots + x_n\)
The Bernoulli distribution is name for Jacob Bernoulli, and governs an indicator random varible. Hence if \(\bs X\) is a random sample of size \(n\) from the distribution then \(\bs X\) is a sequence of \(n\) Bernoulli trials. A separate chapter studies Bernoulli trials in more detail.
Recall that the geometric distribution on \(\N_+\) with parameter \(p \in (0, 1)\) has probability density function \(g\) given by \(g(x) = p (1 - p)^{x - 1}\) for \(x \in \N_+\). Let \(\bs X = (X_1, X_2, \ldots, X_n)\) be a random sample of size \(n \in \N_+\) from the distribution. Give the probability density function of \(\bs X\) in simplified form.
Answer
\(\bs X\) has pdf \(f\) given by \(f(x_1, x_2, \ldots, x_n) = p^n (1 - p)^{y-n}\) for \((x_1, x_2, \ldots, x_n) \in \N_+^n\), where \(y = x_1 + x_2 + \cdots + x_n\).
The geometric distribution governs the trial number of the first success in a sequence of Bernoulli trials. Hence the variables in the random sample can be interpreted as the number of trials between successive successes.
Recall that the Poisson distribution with parameter \(a \in (0, \infty)\) has probability density function \(g\) given by \(g(x) = e^{-a} \frac{a^x}{x!}\) for \(x \in \N\). Let \(\bs X = (X_1, X_2, \ldots, X_n)\) be a random sample of size \(n \in \N_+\) from the distribution. Give the probability density funcion of \(\bs X\) in simplified form.
Answer
\(\bs X\) has PDF \(f\) given by \(f(x_1, x_2, \ldots, x_n) = \frac{1}{x_1! x_2! \cdots x_n!} e^{-n a} a^y\) for \((x_1, x_2, \ldots, x_n) \in \N^n\), where \(y = x_1 + x_2 + \cdots + x_n\).
The Poisson distribution is named for Simeon Poisson, and governs the number of random points in a region of time or space under appropriate circumstances. The parameter \( a \) is proportional to the size of the region. The Poisson distribution is studied in more detail in the chapter on the Poisson process.
Recall again that the exponential distribution with rate parameter \(r \in (0, \infty)\) has probability density function \(g\) given by \(g(x) = r e^{-r x}\) for \(x \in (0, \infty)\). Let \(\bs X = (X_1, X_2, \ldots, X_n)\) be a random sample of size \(n \in \N_+\) from the distribution. Give the probability density funcion of \(\bs X\) in simplified form.
Answer
\(\bs X\) has PDF \(f\) given by \(f(x_1, x_2, \ldots, x_n) = r^n e^{-r y}\) for \((x_1, x_2, \ldots, x_n) \in [0, \infty)^n\), where \(y = x_1 + x_2 + \cdots + x_n\).
The exponential distribution governs failure times and other types or arrival times under appropriate circumstances. The exponential distribution is studied in more detail in the chapter on the Poisson process. The variables in the random sample can be interpreted as the times between successive arrivals in the Poisson process.
Recall that the standard normal distribution has probability density function \(\phi\) given by \(\phi(z) = \frac{1}{\sqrt{2 \pi}} e^{-z^2 / 2}\) for \(z \in \R\). Let \(\bs Z = (Z_1, Z_2, \ldots, Z_n)\) be a random sample of size \(n \in \N_+\) from the distribution. Give the probability density funcion of \(\bs Z\) in simplified form.
Answer
\(\bs Z\) has PDF \(f\) given by \(f(z_1, z_2, \ldots, z_n) = \frac{1}{(2 \pi)^{n/2}} e^{-\frac{1}{2} w^2}\) for \((z_1, z_2, \ldots, z_n) \in \R^n\), where \(w^2 = z_1^2 + z_2^2 + \cdots + z_n^2\).
The standard normal distribution governs physical quantities, properly scaled and centered, subject to small, random errors. The normal distribution is studied in more generality in the chapter on the Special Distributions.
Data Analysis Exercises
For the cicada data, \(G\) denotes gender and \(S\) denotes species type.
- Find the empirical density of \((G, S)\).
- Find the empirical density of \(G\).
- Find the empirical density of \(S\).
- Do you believe that \(S\) and \(G\) are independent?
Answer
The empirical joint and marginal empirical densities are given in the table below. Gender and species are probably dependent (compare the joint density with the product of the marginal densities).
| \(f(i, j)\) | \(i = 0\) | 1 | \(h(j)\) |
|---|---|---|---|
| \(j = 0\) | \(\frac{16}{104}\) | \(\frac{28}{104}\) | \(\frac{44}{104}\) |
| 1 | \(\frac{3}{104}\) | \(\frac{3}{104}\) | \(\frac{6}{104}\) |
| 2 | \(\frac{40}{104}\) | \(\frac{14}{104}\) | \(\frac{56}{104}\) |
| \(g(i)\) | \(\frac{59}{104}\) | \(\frac{45}{104}\) | 1 |
For the cicada data, let \(W\) denote body weight (in grams) and \(L\) body length (in millimeters).
- Construct an empirical density for \((W, L)\).
- Find the corresponding empirical density for \(W\).
- Find the corresponding empirical density for \(L\).
- Do you believe that \(W\) and \(L\) are independent?
Answer
The empirical joint and marginal densities, based on simple partitions of the body weight and body length ranges, are given in the table below. Body weight and body length are almost certainly dependent.
| Density \((W, L)\) | \(w \in (0, 0.1]\) | \((0.1, 0.2]\) | \((0.2, 0.3]\) | \((0.3, 0.4]\) | Density \(L\) |
|---|---|---|---|---|---|
| \(l \in (15, 20]\) | 0 | 0.0385 | 0.0192 | 0 | 0.0058 |
| \((20, 25]\) | 0.1731 | 0.9808 | 0.4231 | 0 | 0.1577 |
| \((25, 30]\) | 0 | 0.1538 | 0.1731 | 0.0192 | 0.0346 |
| \((30, 35]\) | 0 | 0 | 0 | 0.0192 | 0.0019 |
| Density \(W\) | 0.8654 | 5.8654 | 3.0769 | 0.1923 |
For the cicada data, let \(G\) denote gender and \(W\) body weight (in grams).
- Construct and empirical density for \((W, G)\).
- Find the empirical density for \(G\).
- Find the empirical density for \(W\).
- Do you believe that \(G\) and \(W\) are independent?
Answer
The empirical joint and marginal densities, based on a simple partition of the body weight range, are given in the table below. Body weight and gender are almost certainly dependent.
| Density \((W, G)\) | \(w \in (0, 0.1]\) | \((0.1, 0.2]\) | \((0.2, 0.3]\) | \((0.3, 0.4]\) | Density \(G\) |
|---|---|---|---|---|---|
| \(g = 0\) | 0.1923 | 2.5000 | 2.8846 | 0.0962 | 0.5673 |
| 1 | 0.6731 | 3.3654 | 0.1923 | 0.0962 | 0.4327 |
| Density \(W\) | 0.8654 | 5.8654 | 3.0769 | 0.1923 |


