2.7: Measure Spaces
- Page ID
- 10135
In this section we discuss positive measure spaces (which include probability spaces) from a more advanced point of view. The sections on Measure Theory and Special Set Structures in the chapter on Foundations are essential prerequisites. On the other hand, if you are not interested in the measure-theoretic aspects of probability, you can safely skip this section.
Positive Measure
Definitions
Suppose that \( S \) is a set, playing the role of a universal set for a mathematical theory. As we have noted before, \( S \) usually comes with a \( \sigma \)-algebra \( \mathscr S \) of admissible subsets of \( S \), so that \( (S, \mathscr S) \) is a measurable space. In particular, this is the case for the model of a random experiment, where \( S \) is the set of outcomes and \( \mathscr S \) the \( \sigma \)-algebra of events, so that the measurable space \( (S, \mathscr S) \) is the sample space of the experiment. A probability measure is a special case of a more general object known as a positive measure.
A positive measure on \((S, \mathscr S)\) is a function \(\mu: \mathscr S \to [0, \infty] \) that satisfies the following axioms:
- \( \mu(\emptyset) = 0 \)
- If \(\{A_i: i \in I\}\) is a countable, pairwise disjoint collection of sets in \(\mathscr S\) then \[\mu\left(\bigcup_{i \in I} A_i\right) = \sum_{i \in I} \mu(A_i)\]
The triple \((S, \mathscr S, \mu)\) is a measure space.
Axiom (b) is called countable additivity, and is the essential property. The measure of a set that consists of a countable union of disjoint pieces is the sum of the measures of the pieces. Note also that since the terms in the sum are positive, there is no issue with the order of the terms in the sum, although of course, \( \infty \) is a possible value.
.png?revision=1)
So perhaps the term measurable space for \( (S, \mathscr S) \) makes a little more sense now—a measurable space is one that can have a positive measure defined on it.
Suppose that \( (S, \mathscr S, \mu) \) is a measure space.
- If \( \mu(S) \lt \infty \) then \( (S, \mathscr S, \mu) \) is a finite measure space.
- If \( \mu(S) = 1 \) then \( (S, \mathscr S, \mu) \) is a probability space.
So probability measures are positive measures, but positive measures are important beyond the application to probability. The standard measures on the Euclidean spaces are all positive measures: the extension of length for measurable subsets of \( \R \), the extension of area for measurable subsets of \( \R^2 \), the extension of volume for measurable subsets of \( \R^3 \), and the higher dimensional analogues. We will actually construct these measures in the next section on Existence and Uniqueness. In addition, counting measure \( \# \) is a positive measure on the subsets of a set \( S \). Even more general measures that can take positive and negative values are explored in the chapter on Distributions.
Properties
The following results give some simple properties of a positive measure space \( (S, \mathscr S, \mu) \). The proofs are essentially identical to the proofs of the corresponding properties of probability, except that the measure of a set may be infinite so we must be careful to avoid the dreaded indeterminate form \( \infty - \infty \).
If \( A, \, B \in \mathscr S \), then \( \mu(B) = \mu(A \cap B) + \mu(B \setminus A) \).
Proof
Note that \( B = (A \cap B) \cup (B \setminus A) \), and the sets in the union are disjoint.
If \( A, \, B \in \mathscr S \) and \( A \subseteq B \) then
- \( \mu(B) = \mu(A) + \mu(B \setminus A) \)
- \( \mu(A) \le \mu(B) \)
Proof
Part (a) follows from the previous theorem, since \( A \cap B = A \). Part (b) follows from part (a).
Thus \( \mu \) is an increasing function, relative to the subset partial order \( \subseteq \) on \( \mathscr S \) and the ordinary order \( \le \) on \( [0, \infty] \). In particular, if \( \mu \) is a finite measure, then \( \mu(A) \lt \infty \) for every \( A \in \mathscr S \). Note also that if \( A, \, B \in \mathscr S \) and \( \mu(B) \lt \infty \) then \( \mu(B \setminus A) = \mu(B) - \mu(A \cap B) \). In the special case that \( A \subseteq B \), this becomes \( \mu(B \setminus A) = \mu(B) - \mu(A) \). In particular, these results holds for a finite measure and are just like the difference rules for probability. If \( \mu \) is a finite measure, then \( \mu(A^c) = \mu(S) - \mu(A) \). This is the analogue of the complement rule in probability, with but with \( \mu(S) \) replacing 1.
The following result is the analogue of Boole's inequality for probability. For a general positive measure, the result is referred to as the subadditive property.
Suppose that \( A_i \in \mathscr S \) for \( i \) in a countable index set \( I \). Then \[ \mu\left(\bigcup_{i \in I} A_i \right) \le \sum_{i \in I} \mu(A_i) \]
Proof
The proof is exaclty like the one for Boole's inequality. Assume that \( I = \N_+ \). Let \( B_1 = A_1 \) and \( B_i = A_i \setminus (A_1 \cup \ldots \cup A_{i-1}) \) for \( i \in \{2, 3, \ldots\} \). Then \( \{B_i: i \in I\} \) is a disjoint collection of sets in \( \mathscr S \) with the same union as \( \{A_i: i \in I\} \). Also \( B_i \subseteq A_i \) for each \( i \) so \( \mu(B_i) \le \mu(A_i) \). Hence \[ \mu\left(\bigcup_{i \in I} A_i \right) = \mu\left(\bigcup_{i \in I} B_i \right) = \sum_{i \in I} \mu(B_i) \le \sum_{i \in I} \mu(A_i) \]
For a union of sets with finite measure, the inclusion-exclusion formula holds, and the proof is just like the one for probability.
Suppose that \(A_i \in \mathscr S\) for each \(i \in I\) where \(\#(I) = n\), and that \( \mu(A_i) \lt \infty \) for \( i \in I \). Then \[\mu \left( \bigcup_{i \in I} A_i \right) = \sum_{k = 1}^n (-1)^{k - 1} \sum_{J \subseteq I, \; \#(J) = k} \mu \left( \bigcap_{j \in J} A_j \right)\]
Proof
The proof is by induction on \(n\). The proof for \( n = 2 \) is simple: \( A_1 \cup A_2 = A_1 \cup (A_2 \setminus A_1) \). The union on the right is disjoint, so using additivity and the difference rule, \[ \mu(A_1 \cup A_2) = \mu (A_1) + \mu(A_2 \setminus A_1) = \mu(A_1) + \mu(A_2) - \mu(A_1 \cap A_2) \] Suppose now that the inclusion-exclusion formula holds for a given \( n \in \N_+ \), and consider the case \( n + 1 \). Then \[ \bigcup_{i=1}^{n + 1} A_i = \left(\bigcup_{i=1}^n A_i \right) \cup \left[ A_{n+1} \setminus \left(\bigcup_{i=1}^n A_i\right) \right] \] As before, the set in parentheses and the set in square brackets are disjoint. Thus using the additivity axiom, the difference rule, and the distributive rule we have \[ \mu\left(\bigcup_{i=1}^{n+1} A_i\right) = \mu\left(\bigcup_{i=1}^n A_i\right) + \mu(A_{n+1}) - \mu\left(\bigcup_{i=1}^n (A_{n+1} \cap A_i) \right) \] By the induction hypothesis, the inclusion-exclusion formula holds for each union of \( n \) sets on the right. Applying the formula and simplifying gives the inclusion-exclusion formula for \( n + 1 \) sets.
The continuity theorem for increasing sets holds for a positive measure. The continuity theorem for decreasing events holds also, if the sets have finite measure. Again, the proofs are similar to the ones for a probability measure, except for considerations of infinite measure.
Suppose that \( (A_1, A_2, \ldots) \) is a sequence of sets in \( \mathscr S \).
- If the sequence is increasing then \( \mu\left(\bigcup_{i=1}^\infty A_i \right) = \lim_{n \to \infty} \mu(A_n) \).
- If sequence is decreasing and \( \mu(A_1) \lt \infty \) then \( \mu\left(\bigcap_{i=1}^\infty A_i \right) = \lim_{n \to \infty} \mu(A_n) \).
Proof
- Note that if \( \mu(A_k) = \infty \) for some \( k \) then \( \mu(A_n) = \infty \) for \( n \ge k \) and \( \mu\left(\bigcup_{i=1}^\infty A_i \right) = \infty \). Thus, suppose that \( \mu(A_i) \lt \infty \) for each \( i \). Let \( B_1 = A_1 \) and \( B_i = A_i \setminus A_{i-1} \) for \( i \in \{2, 3, \ldots\} \). Then \( (B_1, B_2, \ldots) \) is a disjoint sequence with the same union as \( (A_1, A_2, \ldots) \). Also, \( \mu(B_1) = \mu(A_1) \) and by the proper difference rule, \( \mu(B_i) = \mu(A_i) - \mu(A_{i-1}) \) for \( i \in \{2, 3, \ldots\} \). Hence \[ \mu\left(\bigcup_{i=1}^\infty A_i \right) = \mu \left(\bigcup_{i=1}^\infty B_i \right) = \sum_{i=1}^\infty \mu(B_i) = \lim_{n \to \infty} \sum_{i=1}^n \mu(B_i) \] But \( \sum_{i=1}^n \mu(B_i) = \mu(A_1) + \sum_{i=2}^n [\mu(A_i) - \mu(A_{i-1})] = \mu(A_n) \).
- Note that \( A_1 \setminus A_n \) is increasing in \( n \). Hence using the continuity result for increasing sets, \begin{align} \mu \left(\bigcap_{i=1}^\infty A_i \right) & = \mu\left[A_1 \setminus \bigcup_{i=1}^\infty (A_1 \setminus A_i) \right] = \mu(A_1) - \mu\left[\bigcup_{i=1}^\infty (A_1 \setminus A_n)\right]\\ & = \mu(A_1) - \lim_{n \to \infty} \mu(A_1 \setminus A_n) = \mu(A_1) - \lim_{n \to \infty} \left[\mu(A_1) - \mu(A_n)\right] = \lim_{n \to \infty} \mu(A_n) \end{align}
Recall that if \( (A_1, A_2, \ldots) \) is increasing, \( \bigcup_{i=1}^\infty A_i \) is denoted \( \lim_{n \to \infty} A_n \), and if \( (A_1, A_2, \ldots) \) is decreasing, \( \bigcap_{i=1}^\infty A_i \) is denoted \( \lim_{n \to \infty} A_n \). In both cases, the continuity theorem has the form \( \mu\left(\lim_{n \to \infty} A_n\right) = \lim_{n \to \infty} \mu(A_n) \). The continuity theorem for decreasing events fails without the additional assumption of finite measure. A simple counterexample is given below.
The following corollary of the inclusion-exclusion law gives a condition for countable additivity that does not require that the sets be disjoint, but only that the intersections have measure 0. The result is used below in the theorem on completion.
Suppose that \( A_i \in \mathscr S \) for each \( i \) in a countable index set \( I \) and that \( \mu(A_i) \lt \infty \) for \( i \in I \) and \( \mu(A_i \cap A_j) = 0 \) for distinct \( i, \, j \in I \). Then \[ \mu\left(\bigcup_{i \in I} A_i \right) = \sum_{i \in I} \mu(A_i) \]
Proof
We will assume that \( I = \N_+ \). For \( n \in \N_+ \), \[ \mu\left(\bigcup_{i=1}^n A_i\right) = \sum_{i=1}^n \mu(A_i) \] as an immediate consequence of the inclusion-exclusion law, under the assumption that \( \mu(A_i \cap A_j) = 0 \) for distinct \( i, j \in \{1, 2, \ldots, n\} \). Next \( \bigcup_{i=1}^n A_i \uparrow \bigcup_{i=1}^\infty A_i \) as \( n \to \infty \), and hence by the continuity theorem for increasing events, \( \mu\left(\bigcup_{i=1}^n A_i\right) \to \mu\left(\bigcup_{i=1}^\infty A_i\right) \) as \( n \to \infty \). On the other hand, \( \sum_{i=1}^n \mu(A_i) \to \sum_{i=1}^\infty \mu(A_i) \) as \( n \to \infty \) by the definition of an infinite series of nonnegative terms.
More Definitions
If a positive measure is not finite, then the following definition gives the next best thing.
The measure space \( (S, \mathscr S, \mu) \) is \( \sigma \)-finite if there exists a countable collection \(\{A_i: i \in I\} \subseteq \mathscr S\) with \( \bigcup_{i \in I} A_i = S \) and \( \mu(A_i) \lt \infty \) for each \( i \in I \).
So of course, if \(\mu\) is a finite measure on \((S, \mathscr S)\) then \(\mu\) is \(\sigma\)-finite, but not conversely in general. On the other hand, for \( i \in I \), let \( \mathscr S_i = \{A \in \mathscr S: A \subseteq A_i\} \). Then \( \mathscr S_i \) is a \( \sigma \)-algebra of subsets of \( A_i \) and \( \mu \) restricted to \( \mathscr S_i \) is a finite measure. The point of this (and the reason for the definition) is that often nice properties of finite measures can be extended to \( \sigma \)-finite measures. In particular, \( \sigma \)-finite measure spaces play a crucial role in the construction of product measure spaces, and for the completion of a measure space considered below.
Suppose that \( (S, \mathscr S, \mu) \) is a \( \sigma \)-finite measure space.
- There exists an increasing sequence satisfying the \( \sigma \)-finite definition
- There exists a disjoint sequence satisfying the \( \sigma \)-finite definition.
Proof
Without loss of generality, we can take \(\N_+\) as the index set in the definition. So there exists \( A_n \in \mathscr S\) for \(n \in \N_+ \) such that \( \mu(A_n) \lt \infty \) for each \( n \in \N_+ \) and \( S = \bigcup_{n=1}^\infty A_n \). The proof uses some of the same tricks that we have seen before.
- Let \( B_n = \bigcup_{i = 1}^n A_i \). Then \( B_n \in \mathscr S \) for \( n \in \N_+ \) and this sequence is increasing. Moreover, \( \mu(B_n) \le \sum_{i=1}^n \mu(A_i) \lt \infty \) for \( n \in \N_+ \) and \( \bigcup_{n=1}^\infty B_n = \bigcup_{n=1}^\infty A_n = S \).
- Let \( C_1 = A_1 \) and let \( C_n = A_n \setminus \bigcup_{i=1}^{n-1} A_i \) for \( n \in \{2, 3, \ldots\} \). Then \( C_n \in \mathscr S \) for each \( n \in \N_+ \) and this sequence is disjoint. Moreover, \( C_n \subseteq A_n \) so \( \mu(C_n) \le \mu(A_n) \lt \infty \) and \( \bigcup_{n=1}^\infty C_n = \bigcup_{n=1}^\infty A_n = S \).
Our next definition concerns sets where a measure is concentrated, in a certain sense.
Suppose that \((S, \mathscr S, \mu)\) is a measure space. An atom of the space is a set \(A \in \mathscr S\) with the following properties:
- \(\mu(A) \gt 0\)
- If \(B \in \mathscr S\) and \(B \subseteq A\) then either \(\mu(B) = \mu(A)\) or \(\mu(B) = 0\).
A measure space that has no atoms is called non-atomic or diffuse.
In probability theory, we are often particularly interested in atoms that are singleton sets. Note that \( \{x\} \in \mathscr S \) is an atom if and only if \( \mu(\{x\}) \gt 0 \), since the only subsets of \( \{x\} \) are \( \{x\} \) itself and \( \emptyset \).
Constructions
There are several simple ways to construct new positive measures from existing ones. As usual, we start with a measurable space \( (S, \mathscr S) \).
Suppose that \( (R, \mathscr R) \) is a measurable subspace of \( (S, \mathscr S) \). If \( \mu \) is a positive measure on \( (S, \mathscr S) \) then \( \mu \) restricted to \( \mathscr R \) is a positive measure on \( (R, \mathscr R) \). If \( \mu \) is a finite measure on \( (S, \mathscr S) \) then \( \mu \) is a finite measure on \( (R, \mathscr R) \).
Proof
The assumption is that \( \mathscr R \) is a \( \sigma \)-algebra of subsets of \( R \) and \( \mathscr R \subseteq \mathscr S \). In particular \( R \in \mathscr S \). Since the additivity property of \( \mu \) holds for a countable, disjoint collection of events in \( \mathscr S \), it trivially holds for a countable, disjoint collection of events in \( \mathscr R \). Finally, by the increasing property, \( \mu(R) \le \mu(S) \) so if \( \mu(S) \lt \infty \) then \( \mu(R) \lt \infty \).
However, if \(\mu\) is \(\sigma\)-finite on \( (S, \mathscr S) \), it is not necessarily true that \(\mu\) is \(\sigma\)-finite on \( (R, \mathscr R) \). A counterexample is given below. The previous theorem would apply, in particular, when \( R = S \) so that \( \mathscr R \) is a sub \( \sigma \)-algebra of \( \mathscr S \). Next, a positive multiple of a positive measure gives another positive measure.
If \( \mu \) is a positive measure on \( (S, \mathscr S) \) and \( c \in (0, \infty) \), then \( c \mu \) is also a positive measure on \( (S, \mathscr S) \). If \( \mu \) is finite (\( \sigma \)-finite) then \( c \mu \) is finite (\( \sigma \)-finite) respectively.
Proof
Clearly \( c \mu: \mathscr S \to [0, \infty] \). Also \( (c \mu)(\emptyset) = c \mu(\emptyset) = 0 \). Next if \( \{A_i: i \in I\} \) is a countable, disjoint collection of events in \( \mathscr S \) then \[ (c \mu)\left(\bigcup_{i \in I} A_i\right) = c \mu\left(\bigcup_{i \in I} A_i\right) = c \sum_{i \in I} \mu(A_i) = \sum_{i \in I} c \mu(A_i) \] Finally, since \( \mu(A) \lt \infty \) if and only if \( (c \mu)(A) \lt \infty \) for \( A \in \mathscr S \), the finiteness and \( \sigma \)-finiteness properties are trivially preserved.
A nontrivial finite positive measure \( \mu \) is practically just like a probability measure, and in fact can be re-scaled into a probability measure \( \P \), as was done in the section on Probability Measures:
Suppose that \( \mu \) is a positive measure on \( (S, \mathscr S) \) with \( 0 \lt \mu(S) \lt \infty \). Then \( \P \) defined by \( \P(A) = \mu(A) / \mu(S) \) for \( A \in \mathscr S \) is a probability measure on \( (S, \mathscr S) \).
Proof
\( \P \) is a measure by the previous result, and trivially \( \P(S) = 1 \).
Sums of positive measures are also positive measures.
If \( \mu_i \) is a positive measure on \( (S, \mathscr S) \) for each \( i \) in a countable index set \( I \) then \( \mu = \sum_{i \in I} \mu_i \) is also a positive measure on \( (S, \mathscr S) \).
- If \( I \) is finite and \( \mu_i \) is finite for each \(i \in I\) then \(\mu\) is finite.
- If \( I \) is finite and \(\mu_i\) is \( \sigma \)-finite for each \( i \in I \) then \( \mu \) is \( \sigma \)-finite.
Proof
Clearly \( \mu: \mathscr S \to [0, \infty] \). First \( \mu(\emptyset) = \sum_{i \in I} \mu_i(\emptyset) = 0 \). Next if \( \{A_j: j \in J\} \) is a countable, disjoint collection of events in \( \mathscr S \) then \[ \mu\left(\bigcup_{j \in J} A_j\right) = \sum_{i \in I} \mu_i \left(\bigcup_{j \in J} A_j\right) = \sum_{i \in I} \sum_{j \in J} \mu_i(A_j) = \sum_{j \in J} \sum_{i \in I} \mu_i(A_j) = \sum_{j \in J} \mu(A_j) \] The interchange of sums is permissible since the terms are nonnegative. Suppose now that \( I \) is finite.
- If \( \mu_i \) is finite for each \( i \in I \) then \( \mu(S) = \sum_{i \in I} \mu_i(S) \lt \infty \) so \( \mu \) is finite.
- Suppose that \( \mu_i \) is \( \sigma \)-finite for each \( i \in I \). Then for each \( i \in I \) there exists a collection \( \mathscr A_i = \{A_{i j}: j \in \N\} \subseteq \mathscr S \) such that \( \bigcup_{j=1}^\infty A_{i j} = S \) and \( \mu_i(A_{i j}) \lt \infty \) for each \( j \in \N \). For \( j \in \N \), let \( B_j = \bigcap_{i \in I} A_{i,j} \). Then \( B_j \in \mathscr S \) for each \( j \in \N \) and \[ \bigcup_{j=1}^\infty B_j = \bigcup_{j=1}^\infty \bigcap_{i \in I} A_{i j} = \bigcap_{i \in I} \bigcup_{j=1}^\infty A_{i j} = \bigcap_{i \in I} S = S \] Moreover, \[ \mu(B_j) = \sum_{i \in I} \mu_i(B_j) \le \sum_{i \in I} \mu_i(A_{i j}) \lt \infty \] so \( \mu \) is \( \sigma \)-finnite.
In the context of the last result, if \(I\) is countably infinite and \(\mu_i\) is finite for each \(i \in I\), then \(\mu\) is not necessarily \(\sigma\)-finite. A counterexample is given below. In this case, \(\mu\) is said to be \(s\)-finite, but we've had enough definitions, so we won't pursue this one. From scaling and sum properties, note that a positive linear combination of positive measures is a positive measure. The next method is sometimes referred to as a change of variables.
Suppose that \( (S, \mathscr S, \mu) \) is a measure space. Suppose also that \( (T, \mathscr T) \) is another measurable space and that \( f: S \to T \) is measurable. Then \( \nu \) defined as follows is a positive measure on \( (T, \mathscr T) \) \[ \nu(B) = \mu\left[f^{-1}(B)\right], \quad B \in \mathscr T \] If \( \mu \) is finite then \( \nu \) is finite.
Proof
Clearly \(\nu: \mathscr T \to [0, \infty]\). The proof is easy since inverse images preserve all set operations. First \( f^{-1}(\emptyset) = \emptyset \) so \( \nu(\emptyset) = 0 \). Next, if \( \left\{B_i: i \in I\right\} \) is a countable, disjoint collection of sets in \( \mathscr T \), then \( \left\{f^{-1}(B_i): i \in I\right\} \) is a countable, disjoint collection of sets in \( \mathscr S \), and \( f^{-1}\left(\bigcup_{i \in I} B_i\right) = \bigcup_{i \in I} f^{-1}(B_i) \). Hence \[ \nu\left(\bigcup_{i \in I} B_i\right) = \mu\left[f^{-1}\left(\bigcup_{i \in I} B_i\right)\right] = \mu\left[\bigcup_{i \in I} f^{-1}(B_i)\right] = \sum_{i \in I} \mu\left[f^{-1}(B_i)\right] = \sum_{i \in I} \nu(B_i) \] Finally, if \(\mu\) is finite then \(\nu(T) = \mu[f^{-1}(T)] = \mu(S) \lt \infty\) so \(\nu\) is finite.
In the context of the last result, if \(\mu\) is \(\sigma\)-finite on \((S, \mathscr S)\), it is not necessarily true that \(\nu\) is \(\sigma\)-finite on \((T, \mathscr T)\), even if \(f\) is one-to-one. A counterexample is given below. The takeaway is that \(\sigma\)-finiteness of \(\nu\) depends very much on the nature of the \(\sigma\)-algebra \(\mathscr T\). Our next result shows that it's easy to explicitly construct a positive measure on a countably generated \( \sigma \)-algebra, that is, a \( \sigma \)-algebra generated by a countable partition. Such \( \sigma \)-algebras are important for counterexamples and to gain insight, and also because many \( \sigma \)-algebras that occur in applications can be constructed from them.
Suppose that \( \mathscr A = \{A_i: i \in I\} \) is a countable partition of \( S \) into nonempty sets, and that \( \mathscr S = \sigma(\mathscr{A}) \), the \( \sigma \)-algebra generated by the partition. For \( i \in I \), define \( \mu(A_i) \in [0, \infty] \) arbitrarily. For \( A = \bigcup_{j \in J} A_j \) where \( J \subseteq I \), define \[ \mu(A) = \sum_{j \in J} \mu(A_j) \] Then \( \mu \) is a positive measure on \( (S, \mathscr S) \).
- The atoms of the measure are the sets of the form \(A = \bigcup_{j \in J} A_j\) where \(J \subseteq I\) and where \(\mu(A_j) \gt 0\) for one and only one \(j \in J\).
- If \(\mu(A_i) \lt \infty\) for \(i \in I\) and \(I\) is finite then \(\mu\) is finite.
- If \(\mu(A_i) \lt \infty\) for \(i \in I\) and \(I\) is countably infinite then \(\mu\) is \(\sigma\)-finite.
Proof
Recall that every \( A \in \mathscr S \) has a unique representation of the form \( A = \bigcup_{j \in J} A_j \) where \( J \subseteq I \). In particular, \( J = \emptyset \) in this representation gives \( A = \emptyset \). The sum over an empty index set is 0, so \( \mu(\emptyset) = 0 \). Next suppose that \( \{B_k: k \in K\} \) is a countable, disjoint collection of sets in \( \mathscr S \). Then there exists a disjoint collection \(\{J_k: k \in K\}\) of subsets of \(I\) such that \( B_k = \bigcup_{j \in J_k} A_j \). Hence \[ \mu\left(\bigcup_{k \in K} B_k\right) = \mu\left(\bigcup_{k \in K} \bigcup_{j \in J_k} A_j\right) = \sum_{k \in k}\sum_{j \in J_k} \mu(A_j) = \sum_{k \in K} \mu(B_k) \] The fact that the terms are all nonnegative means that we do not have to worry about the order of summation.
- Again, every \(A \in \mathscr S\) has the unique representation \(A = \bigcup_{j \in J} A_j\) where \(J \subseteq I\). The subsets of \(A\) that are in \(\mathscr S\) are \(\bigcup_{k \in K} A_k\) ahere \(K \subseteq J\). Hence \(A\) is an atom if and only if \(\mu(A_j) \gt 0\) for one and only one \(j \in J\).
- If \(I\) is finite and \(\mu(A_i) \lt \infty\) then \(\mu(S) = \sum_{i \in I} \mu(A_i) \lt \infty\), so \(\mu\) is finite.
- If \(I\) is countabley infinite and \(\mu(A_i) \lt \infty\) for \(i \in I\) then \(\mathscr A\) satisfies the condition for \(\mu\) to be \(\sigma\)-finite.
One of the most general ways to construct new measures from old ones is via the theory of integration with respect to a positive measure, which is explored in the chapter on Distributions. The construction of positive measures more or less from scratch
is considered in the next section on Existence and Uniqueness. We close this discussion with a simple result that is useful for counterexamples.
Suppose that the measure space \( (S, \mathscr S, \mu) \) has an atom \( A \in \mathscr S \) with \( \mu(A) = \infty \). Then the space is not \( \sigma \)-finite.
Proof
Let \( \{A_i: i \in I\} \) be a countable disjoint collection of sets in \( \mathscr S \) that partitions \( S \). Then \( \{A \cap A_i: i \in I\} \) partitions \( A \). Since \( \mu(A) = \sum_{i \in I} \mu(A \cap A_i) \), we must have \( \mu(A \cap A_i) \gt 0 \) for some \( i \in I \). Since \( A \) is an atom and \( A \cap A_i \subseteq A \) it follows that \( \mu(A \cap A_i) = \infty \). Hence also therefore \( \mu(A_i) = \infty \).
Measure and Topology
Often the spaces that occur in probability and stochastic processes are topological spaces. Recall that a topological space \( (S, \mathscr T) \) consists of a set \( S \) and a topology \( \mathscr T \) on \( S \) (the collection of open sets). The topology as well as the measure theory plays an important role, so it's natural to want these two types of structures to be compatible. We have already seen the most important step in this direction: Recall that \( \mathscr S = \sigma(\mathscr T) \), the \( \sigma \)-algebra generated by the topology, is the Borel \( \sigma \)-algebra on \( S \), named for Émile Borel. Since the complement of an open set is a closed set, \(\mathscr S\) is also the \(\sigma\)-algebra generated by the collection of closed sets. Moreover, \(\mathscr S\) contains countable intersections of open sets (called \(G_\delta\) sets) and countable unions of closed sets (called \(F_\sigma\) sets).
Suppose that \( (S, \mathscr T) \) is a topological space and let \(\mathscr S = \sigma(\mathscr T)\) be the Borel \(\sigma\)-algebra. A positive measure \( \mu \) on \( (S, \mathscr S) \) is a Borel measure and then \((S, \mathscr S, \mu)\) is a Borel measure space.
The next definition concerns the subset on which a Borel measure is concentrated, in a certain sense.
Suppose that \((S, \mathscr S, \mu)\) is a Borel measure space. The support of \(\mu\) is \[\supp(\mu) = \{x \in S: \mu(U) \gt 0 \text{ for every open neighborhood } U \text{ of } x\}\] The set \(\supp(\mu)\) is closed.
Proof
Let \(A = \supp(\mu)\). For \(x \in A^c\), there exists an open neighborhood \(V_x\) of \(x\) such that \(\mu(V_x) = 0\). If \(y \in V_x\), then \(V_x\) is also an open neighborhood of \(y\), so \(y \in A^c\). Hence \(V_x \subseteq A^c\) for every \(x \in A^c\) and so \( A^c \) is open.
The term Borel measure has different definitions in the literature. Often the topological space is required to be locally compact, Hausdorff, and with a countable base (LCCB). Then a Borel measure \( \mu \) is required to have the additional condition that \( \mu(C) \lt \infty \) if \( C \subseteq S \) is compact. In this text, we use the term Borel measures in this more restricted sense.
Suppose that \((S, \mathscr S, \mu)\) is a Borel measure space corresponding to an LCCB topolgy. Then the space is \(\sigma\)-finite.
Proof
Since the topological space is locally compact and has a countable base, \(S = \bigcup_{i \in I} C_i\) where \(\{C_i: i \in I\}\) is a countable collection of compact sets. Since \(\mu\) is a Borel measure, \(\mu(C_i) \lt \infty\) and hence \(\mu\) is \(\sigma\)-finite.
Here are a couple of other definitions that are important for Borel measures, again linking topology and measure in natural ways.
Suppose again that \( (S, \mathscr S, \mu) \) is a Borel measure space.
- \( \mu \) is inner regular if \( \mu(A) = \sup\{\mu(C): C \text{ is compact and } C \subseteq A\} \) for \( A \in \mathscr S \).
- \( \mu \) is outer regular if \( \mu(A) = \inf\{\mu(U): U \text{ is open and } A \subseteq U\} \) for \( A \in \mathscr S \).
- \( \mu \) is regular if it is both inner regular and outer regular.
The measure spaces that occur in probability and stochastic processes are usually regular Borel spaces associated with LCCB topologies.
Null Sets and Equivalence
Sets of measure 0 in a measure space turn out to be very important precisely because we can often ignore the differences between mathematical objects on such sets. In this disucssion, we assume that we have a fixed measure space \((S, \mathscr S, \mu)\).
A set \(A \in \mathscr S\) is null if \(\mu(A) = 0\).
Consider a measurable statement
with \( x \in S \) as a free variable. (Technically, such a statement is a predicate on \( S \).) If the statement is true for all \( x \in S \) except for \( x \) in a null set, we say that the statement holds almost everywhere on \( S \). This terminology is used often in measure theory and captures the importance of the definition.
Let \( \mathscr D = \{A \in \mathscr S: \mu(A) = 0 \text{ or } \mu(A^c) = 0\}\), the collection of null and co-null sets. Then \( \mathscr D \) is a sub \(\sigma\)-algebra of \( \mathscr S \).
Proof
Trivially \( S \in \mathscr D \) since \(S^c = \emptyset\) and \(\mu(\emptyset) = 0\). Next if \(A \in \mathscr D\) then \(A^c \in \mathscr D\) by the symmetry of the definition. Finally, suppose that \( A_i \in \mathscr D \) for \( i \in I \) where \( I \) is a countable index set. If \( \mu(A_i) = 0 \) for every \( i \in I \) then \( \mu\left(\bigcup_{i \in I} A_i \right) \le \sum_{i \in I} \mu(A_i) = 0 \) by the subadditive property. On the other hand, if \( \mu(A_j^c) = 0 \) for some \( j \in J \) then \( \mu\left[\left(\bigcup_{i \in I} A_i \right)^c\right] = \mu\left(\bigcap_{i \in I} A_i^c\right) \le \mu(A_j^c) = 0 \). In either case, \( \bigcup_{i \in I} A_i \in \mathscr D \).
Of course \(\mu\) restricted to \(\mathscr D\) is not very interesting since \(\mu(A) = 0\) or \(\mu(A) = \mu(S)\) for every \(A \in \mathscr S\). Our next definition is a type of equivalence between sets in \(\mathscr S\). To make this precise, recall first that the symmetric difference between subsets \( A \) and \( B \) of \(S\) is \( A \bigtriangleup B = (A \setminus B) \cup (B \setminus A) \). This is the set that consists of points in one of the two sets, but not both, and corresponds to exclusive or.
Sets \(A, \, B \in \mathscr S\) are equivalent if \(\mu(A \bigtriangleup B) = 0 \), and we denote this by \( A \equiv B \).
Thus \(A \equiv B\) if and only if \(\mu(A \bigtriangleup B) = \mu(A \setminus B) + \mu(B \setminus A) = 0\) if and only if \(\mu(A \setminus B) = \mu(B \setminus A) = 0\). In the predicate terminology mentioned above, the statement \[ x \in A \text{ if and only if } x \in B \] is true for almost every \( x \in S \). As the name suggests, the relation \( \equiv \) really is an equivalence relation on \( \mathscr S \) and hence \( \mathscr S \) is partitioned into disjoint classes of mutually equivalent sets. Two sets in the same equivalence class differ by a set of measure 0.
The relation \( \equiv \) is an equivalence relation on \( \mathscr S \). That is, for \( A, \, B, \, C \in \mathscr S \),
- \(A \equiv A\) (the reflexive property).
- If \(A \equiv B\) then \(B \equiv A\) (the symmetric property).
- If \(A \equiv B\) and \(B \equiv C\) then \(A \equiv C\) (the transitive property).
Proof
- The reflexive property is trivial since \(A \bigtriangleup A = \emptyset\).
- The symmetric property is also trivial since \(A \bigtriangleup B = B \bigtriangleup A\).
- For the transitive property, suppose that \( A \equiv B \) and \( B \equiv C \). Note that \( A \setminus C \subseteq (A \setminus B) \cup (B \setminus C) \), and hence \( \P(A \setminus C) = 0 \). By a symmetric argument, \( \P(C \setminus A) = 0 \).
Equivalence is preserved under the standard set operations.
If \( A, \, B \in \mathscr S \) and \( A \equiv B \) then \( A^c \equiv B^c \).
Proof
Note that \( A^c \setminus B^c = B \setminus A \) and \( B^c \setminus A^c = A \setminus B \), so \( A^c \bigtriangleup B^c = A \bigtriangleup B \).
Suppose that \( A_i, \, B_i \in \mathscr S \) and that \( A_i \equiv B_i \) for \( i \) in a countable index set \( I \). Then
- \( \bigcup_{i \in I} A_i \equiv \bigcup_{i \in I} B_i \)
- \( \bigcap_{i \in I} A_i \equiv \bigcap_{i \in I} B_i \)
Proof
- Note that \[ \left(\bigcup_{i \in I} A_i\right) \bigtriangleup \left(\bigcup_{i \in I} B_i\right) \subseteq \bigcup_{i \in I} (A_i \bigtriangleup B_i) \] To see this, note that if \( x \) is in the set on the left then either \( x \in A_j \) for some \( j \in I \) and \( x \notin B_i \) for every \( i \in I \), or \( x \notin A_i \) for every \( i \in I \) and \( x \in B_j \) for some \( j \in I \). In either case, \( x \in A_j \bigtriangleup B_j \) for some \( j \in I \).
- Similarly \[ \left(\bigcap_{i \in I} A_i\right) \bigtriangleup \left(\bigcap_{i \in I} B_i\right) \subseteq \bigcup_{i \in I} (A_i \bigtriangleup B_i) \] If \( x \) is in the set on the left then \( x \in A_i \) for every \( i \in I \) and \( x \notin B_j \) for some \( j \in I \), or \( x \in B_i \) for every \( i \in I \) or \( x \notin A_j \) for some \( j \in I \). In either case, \( x \in A_j \bigtriangleup B_j \) for some \( j \in I \)
In both parts, the proof is completed by noting that the common set on the right in the displayed equations is null: \[ \mu\left[\bigcup_{i \in I} (A_i \bigtriangleup B_i) \right] \le \sum_{i \in I} \mu(A_i \bigtriangleup B_i) = 0 \]
Equivalent sets have the same measure.
If \( A, \, B \in \mathscr S \) and \(A \equiv B\) then \(\mu(A) = \mu(B)\).
Proof
Note again that \( A = (A \cap B) \cup (A \setminus B) \). If \( A \equiv B \) then \( \mu(A) = \mu(A \cap B) \). By a symmetric argument, \( \mu(B) = \mu(A \cap B) \).
The converse trivially fails, and a counterexample is given below. However, the collection of null sets and the collection of co-null sets do form equivalence classes.
Suppose that \( A \in \mathscr S \).
- If \(\mu(A) = 0\) then \(A \equiv B\) if and only if \(\mu(B) = 0\).
- If \(\mu(A^c) = 0\) then \(A \equiv B\) if and only if \(\mu(B^c) = 0\).
Proof
- Suppose that \( \mu(A) = 0 \) and \( A \equiv B\). Then \( \mu(B) = 0 \) by the result above. Conversely, note that \( A \setminus B \subseteq A \) and \( B \setminus A \subseteq B \) so if \( \mu(A) = \mu(B) = 0 \) then \( \mu(A \bigtriangleup B) = 0 \) so \( A \equiv B \).
- Part (b) follows from part (a) and the result above on complements.
We can extend the notion of equivalence to measruable functions with a common range space. Thus suppose that \( (T, \mathscr T) \) is another measurable space. If \( f, \, g: S \to T \) are measurable, then \( (f, g): S \to T \times T \) is measurable with respect the usual product \( \sigma \)-algebra \( \mathscr T \otimes \mathscr T \). We assume that the diagonal set \( D = \{(y, y): y \in T\} \in \mathscr T \otimes \mathscr T \), which is almost always true in applications.
Measurable functions \(f, \, g: S \to T\) are equivalent if \( \mu\{x \in S: f(x) \ne g(x)\} = 0 \). Again we write \( f \equiv g \).
Details
Note that \(\{x \in S: f(x) \ne g(x)\} = \{x \in S: (f(x), g(x)) \in D\}^c \in \mathscr S\) by our assumption, so the definition makes sense.
In the terminology discussed earlier, \( f \equiv g \) means that \( f(x) = g(x) \) almost everywhere on \( S \). As with measurable sets, the relation \( \equiv \) really does define an equivalence relation on the collection of measurable functions from \(S\) to \(T\). Thus, the collection of such functions is partitioned into disjoint classes of mutually equivalent variables.
The relation \( \equiv \) is an equivalence relation on the collection of measurable functions from \(S\) to \(T\). That is, for measurable \(f, \, g, \, h: S \to T\),
- \(f \equiv f\) (the reflexive property).
- If \(f \equiv g\) then \(g \equiv f\) (the symmetric property).
- If \( f \equiv g\) and \(g \equiv h\) then \(f \equiv h\) (the transitive property).
Proof
Parts (a) and (b) are trivially. For (c) note that \( f(x) = g(x) \) and \( g(x) = h(x) \) implies \( f(x) = h(x) \) for \( x \in S \). Negating this statement gives \( f(x) \ne h(x) \) implies \( f(x) \ne g(x) \) or \( g(x) \ne h(x) \). So \[ \{x \in S: f(x) \ne h(x)\} \subseteq \{x \in S: f(x) \ne g(x)\} \cup \{ x \in S: g(x) \ne h(x)\} \] Since \( f \equiv g \) and \( g \equiv h \), the two sets on the right have measure 0. Hence, so does the set on the left.
Suppose agaom that \(f, \, g: S \to T\) are measurable and that \(f \equiv g\). Then for every \(B \in \mathscr T\), the sets \(f^{-1}(B) \equiv g^{-1}(B)\).
Proof
Note that \( f^{-1}(B) \bigtriangleup g^{-1}(B) \subseteq \{x \in S: f(x) \ne g(x)\} \).
Thus if \( f, \, g: S \to T \) are measurable and \( f \equiv g \), then by the previous result, \(\nu_f = \nu_g\) where \(\nu_f, \, \nu_g\) are the measures on \((T, \mathscr T)\) associated with \( f \) and \( g \), as above. Again, the converse fails with a passion.
It often happens that a definition for functions subsumes the corresponding definition for sets, by considering the indicator functons of the sets. So it is with equivalence. In the following result, we can take \(T = \{0, 1\}\) with \(\mathscr T\) the collection of all subsets.
Suppose that \(A, \, B \in \mathscr S\). Then \(A \equiv B\) if and only if \(\bs{1}_A \equiv \bs{1}_B\).
Proof
Note that \( \left\{x \in S: \bs{1}_A(x) \ne \bs{1}_B(x) \right\} = A \bigtriangleup B \).
Equivalence is preserved under composition. For the next result, suppose that \((U, \mathscr U)\) is yet another measurable space.
Suppose that \(f, \, g: S \to T\) are measurable and that \(h: T \to U\) is measurable. If \(f \equiv g\) then \(h \circ f \equiv h \circ g\).
Proof
Note that \( \{x \in S: h[f(x)] \ne h[g(x)]\} \subseteq \{x \in S: f(x) \ne g(x)\} \).
Suppose again that \( (S, \mathscr S, \mu) \) is a measure space. Let \( \mathscr V \) denote the collection of all measurable real-valued random functions from \( S \) into \( \R \). (As usual, \(\R\) is given the Borel \(\sigma\)-algebra.) From our previous discussion of measure theory, we know that with the usual definitions of addition and scalar multiplication, \( (\mathscr V, +, \cdot) \) is a vector space. However, in measure theory, we often do not want to distinguish between functions that are equivalent, so it's nice to know that the vector space structure is preserved when we identify equivalent functions. Formally, let \( [f] \) denote the equivalence class generated by \( f \in \mathscr V \), and let \( \mathscr W \) denote the collection of all such equivalence classes. In modular notation, \( \mathscr W\) is \(\mathscr V \big/ \equiv \). We define addition and scalar multiplication on \( \mathscr W \) by \[ [f] + [g] = [f + g], \; c [f] = [c f]; \quad f, \, g \in \mathscr V, \; c \in \R \]
\( (\mathscr W, +, \cdot) \) is a vector space.
Proof
All that we have to show is that addition and scalar multiplication are well defined. That is, we must show that the definitions do not depend on the particularly representative of the equivalence class. Then the other properties that define a vector space are inherited from \( (\mathscr V, +, \cdot) \). Thus we must show that if \( f_1 \equiv f_2 \) and \( g_1 \equiv g_2 \), and if \( c \in \R \), then \( f_1 + g_1 \equiv f_2 + g_2 \) and \( c f_1 \equiv c f_2 \). For the first problem, note that \((f_1, g_1)\) and \((f_2, g_2)\) are measurable functions from \(S\) to \(\R^2\). (\(\R^2\) is given the product \(\sigma\)-algebra which also happens to be the Borel \(\sigma\)-algebra corresponding to the standard Euclidean topolgy). Moreover, \((f_1, g_1) \equiv (f_2, g_2)\) since \[\{x \in S: (f_1(x), g_1(x)) \ne (f_2(x), g_2(x))\} = \{x \in S: f_1(x) \ne f_2(x)\} \cup \{x \in S: g_1(x) \ne g_2(x)\}\] But the function \((a, b) \mapsto a + b\) from \(\R^2\) into \(\R\) is measurable and hence from composition property, it follows that \(f_1 + g_1 \equiv f_2 + g_2\). The second problem is easier. The function \(a \mapsto c a\) from \(\R\) into \(\R\) is measurable so again it follos from composition property that \(c f_1 \equiv c f_2\).
Often we don't bother to use the special notation for the equivalence class associated with a function. Rather, it's understood that equivalent functions represent the same object. Spaces of functions in a measure space are studied further in the chapter on Distributions.
Completion
Suppose that \( (S, \mathscr S, \mu) \) is a measure space and let \( \mathscr N = \{A \in \mathscr S: \mu(A) = 0\} \) denote the collection of null sets of the space. If \( A \in \mathscr N \) and \( B \in \mathscr S \) is a subset of \( A \), then we know that \( \mu(B) = 0 \) so \( B \in \mathscr N \) also. However, in general there might be subsets of \( A \) that are not in \( \mathscr S \). This leads naturally to the following definition.
The measure space \( (S, \mathscr S, \mu) \) is complete if \( A \in \mathscr N \) and \( B \subseteq A \) imply \( B \in \mathscr S \) (and hence \( B \in \mathscr N \)).
Our goal in this discussion is to show that if \( (S, \mathscr S, \mu) \) is a \( \sigma \)-finite measure that is not complete, then it can be completed. That is \( \mu \) can be extended to \( \sigma \)-algebra that includes all of the sets in \( \mathscr S \) and all subsets of null sets. The first step is to extend the equivalence relation defined in our previous discussion to \( \mathscr P(S) \).
For \( A, \, B \subseteq S \), define \( A \equiv B \) if and only if there exists \( N \in \mathscr N \) such that \( A \bigtriangleup B \subseteq N \). The relation \( \equiv \) is an equivalence relation on \( \mathscr{P}(S) \): For \( A, \, B, \, C \subseteq S \),
- \( A \equiv A \) (the reflexive property).
- If \( A \equiv B \) then \( B \equiv A \) (the symmetric property).
- If \( A \equiv B \) and \( B \equiv C \) then \( A \equiv C \) (the transitive property).
Proof
- Note that \( A \bigtriangleup A = \emptyset \) and \( \emptyset \in \mathscr N \).
- Suppose that \( A \bigtriangleup B \subseteq N \) where \( N \in \mathscr N \). Then \( B \bigtriangleup A = A \bigtriangleup B \subseteq N\).
- Suppose that \( A \bigtriangleup B \subseteq N_1 \) and \( B \bigtriangleup C \subseteq N_2\) where \( N_1, \; N_2 \in \mathscr N \). Then \( A \bigtriangleup C \subseteq (A \bigtriangleup B) \cup (B \bigtriangleup C) \subseteq N_1 \cup N_2 \), and \( N_1 \cup N_2 \in \mathscr N \).
So the equivalence relation \( \equiv \) partitions \( \mathscr P(S) \) into mutually disjoint equivalence classes. Two sets in an equivalence class differ by a subset of a null set. In particular, \( A \equiv \emptyset \) if and only if \( A \subseteq N \) for some \( N \in \mathscr N \). The extended relation \( \equiv \) is preserved under the set operations, just as before. Our next step is to enlarge the \( \sigma \)-algebra \( \mathscr S \) by adding any set that is equivalent to a set in \( \mathscr S \).
Let \( \mathscr S_0 = \{A \subseteq S: A \equiv B \text{ for some } B \in \mathscr S \} \). Then \( \mathscr S_0 \) is a \( \sigma \)-algebra of subsets of \( S \), and in fact is the \( \sigma \)-algebra generated by \( \mathscr S \cup \{A \subseteq S: A \equiv \emptyset\} \).
Proof
Note that if \( A \in \mathscr S \) then \( A \equiv A \) so \( A \in \mathscr S_0 \). In particular, \( S \in \mathscr S_0 \). Also, \( \emptyset \in \mathscr S \) so if \( A \equiv \emptyset \) then \( A \in \mathscr S_0 \). Suppose that \( A \in \mathscr S_0 \) so that \( A \equiv B \) for some \( B \in \mathscr S \). Then \( B^c \in \mathscr S \) and \( A^c \equiv B^c \) so \( A^c \in \mathscr S_0 \). Next suppose that \( A_i \in \mathscr S_0 \) for \( i \) in a countable index set \( I \). Then for each \( i \in I \) there exists \( B_i \in \mathscr S \) such that \( A_i \equiv B_i \). But then \( \bigcup_{i \in I} B_i \in \mathscr S \) and \( \bigcup_{i \in I} A_i \equiv \bigcup_{i \in I} B_i \), so \( \bigcup_{i \in I} A_i \in \mathscr S_0 \). Therefore \( \mathscr S_0 \) is a \( \sigma \)-algebra of subsets of \( S \). Finally, suppose that \( \mathscr T \) is a \( \sigma \)-algebra of subsets of \( S \) and that \( \mathscr S \cup \{A \subseteq S: A \equiv \emptyset\} \subseteq \mathscr T \). We need to show that \( \mathscr S_0 \subseteq \mathscr T \). Thus, suppose that \( A \in \mathscr S_0 \) Then there exists \( B \in \mathscr S \) such that \( A \equiv B \). But \( B \in \mathscr T \) and \( A \bigtriangleup B \in \mathscr T \) so \( A \cap B = B \setminus (A \bigtriangleup B) \in \mathscr T\). Also \( A \setminus B \in \mathscr T \), so \( A = (A \cap B) \cup (A \setminus B) \in \mathscr T \).
Our last step is to extend \( \mu \) to a positive measure on the enlarged \( \sigma \)-algebra \( \mathscr S_0 \).
Suppose that \( A \in \mathscr S_0 \) so that \( A \equiv B \) for some \( B \in \mathscr S \). Define \( \mu_0(A) = \mu(B) \). Then
- \( \mu_0 \) is well defined.
- \( \mu_0(A) = \mu(A) \) for \( A \in \mathscr S \).
- \( \mu_0 \) is a positive measure on \( \mathscr S_0 \).
The measure space \( (S, \mathscr S_0, \mu_0) \) is complete and is known as the completion of \( (S, \mathscr S, \mu) \).
Proof
- Suppose that \( A \in \mathscr S_0 \) and that \( A \equiv B_1 \) and \( A \equiv B_2 \) where \( B_1, \, B_2 \in \mathscr S \). Then \(B_1 \equiv B_2 \) so by the result above \( \mu(B_1) = \mu(B_2) \). Thus, \( \mu_0 \) is well-defined.
- Next, if \( A \in \mathscr S \) then of course \( A \equiv A \) so \( \mu_0(A) = \mu(A) \).
- Trivially \( \mu_0(A) \ge 0 \) for \( A \in \mathscr S_0 \). Thus we just need to show the countable additivity property. To understand the proof you need to keep several facts in mind: the functions \( \mu \) and \( \mu_0 \) agree on \( \mathscr S \) (property (b)); equivalence is preserved under set operations; equivalent sets have the same value under \( \mu_0 \) (property (a)). Since the measure space \( (S, \mathscr S, \mu) \) is \( \sigma \)-finite, there exists a countable disjoint collection \( \{C_i: i \in I\} \) of sets in \( \mathscr S \) such that \( S = \bigcup_{i \in I} C_i \) and \( \mu(C_i) \lt \infty \) for each \( i \in I \). Suppose first that \( A \in \mathscr S_0 \), so that there exists \( B \in \mathscr S \) with \( A \equiv B \). Then \[\mu_0(A) = \mu_0\left[\bigcup_{i \in I} (A \cap C_i)\right] = \mu\left[\bigcup_{i \in I} (B \cap C_i)\right] = \sum_{i \in I} \mu(B \cap C_i) = \sum_{i \in I} \mu_0(A \cap C_i)\] Suppose next that \( (A_1, A_2, \ldots) \) is a sequence of pairwise disjoint sets in \( \mathscr S_0 \) so that there exists a sequence \( (B_1, B_2, \ldots) \) of sets in \( \mathscr S \) such that \( A_i \equiv B_i \) for each \( i \in \N_+ \). For fixed \( i \in I \), \[ \mu_0\left[\bigcup_{n=1}^\infty (A_n \cap C_i)\right] = \mu_0\left[\bigcup_{n=1}^\infty (B_n \cap C_i)\right] = \mu\left[\bigcup_{n=1}^\infty (B_n \cap C_i)\right] = \sum_{in=1}^\infty \mu(B_n \cap C_i) = \sum_{n=1}^\infty \mu_0(A_n \cap C_i) \] The next-to-the-last equality use the inclusion-exclusion law, since we don't know (and it's probably not true) that the sequence \( (B_1, B_2, \ldots) \) is disjoint. The use of inclusion-exclusion is why we need \( (S, \mathscr S, \mu) \) to be \( \sigma \)-finite. Finally, using the previous displayed equations, \begin{align*} \mu_0\left(\bigcup_{n=1}^\infty A_n\right) & = \sum_{i \in I} \mu_0\left[\left(\bigcup_{n=1}^\infty A_n\right) \cap C_i\right] = \sum_{i \in I} \mu_0\left(\bigcup_{n=1}^\infty A_n \cap C_i \right) \\ & = \sum_{i \in I} \sum_{n=1}^\infty \mu_0(A_n \cap C_i) = \sum_{n=1}^\infty \sum_{i \in I} \mu_0(A_n \cap C_i) = \sum_{n=1}^\infty \mu_0(A_n) \end{align*}
Examples and Exercises
As always, be sure to try the computational exercises and proofs yourself before reading the answers and proofs in the text. Recall that a discrete measure space consists of a countable set, with the \( \sigma \)-algebra of all subsets, and with counting measure \( \# \).
Counterexamples
The continuity theorem for decreasing events can fail if the events do not have finite measure.
Consider \( \Z \) with counting measure \( \# \) on the \( \sigma \)-algebra of all subsets. Let \( A_n = \{ z \in \Z: z \le -n\} \) for \( n \in \N_+ \). The continuity theorem fails for \( (A_1, A_2, \ldots) \).
Proof
The sequence is decreasing and \( \#(A_n) = \infty \) for each \( n \), but \( \# \left(\bigcap_{i=1}^\infty A_i\right) = \#(\emptyset) = 0 \).
Equal measure certainly does not imply equivalent sets.
Suppose that \( (S, \mathscr S, \mu) \) is a measure space with the property that there exist disjoint sets \( A, \, B \in \mathscr S\) such that \( \mu(A) = \mu(B) \gt 0 \). Then \( A \) and \( B \) are not equivalent.
Proof
Note that \( A \bigtriangleup B = A \cup B \) and \( \mu(A \cup B) \gt 0 \).
For a concrete example, we could take \( S = \{0, 1\} \) with counting measure \( \# \) on \( \sigma \)-algebra of all subsets, and \( A = \{0\} \), \( B = \{1\} \).
The \( \sigma \)-finite property is not necessarily inherited by a sub-measure space. To set the stage for the counterexample, let \( \mathscr R \) denote the Borel \( \sigma \)-algebra of \( \R \), that is, the \( \sigma \)-algebra generated by the standard Euclidean topology. There exists a positive measure \( \lambda \) on \( (\R, \mathscr R) \) that generalizes length. The measure \( \lambda \), known as Lebesgue measure, is constructed in the section on Existence. Next let \( \mathscr C \) denote the \( \sigma \)-algebra of countable and co-countable sets: \[ \mathscr C = \{A \subseteq \R: A \text{ is countable or } A^c \text{ is countable}\} \] That \( \mathscr C \) is a \( \sigma \)-algebra was shown in the section on measure theory in the chapter on foundations.
\( (\R, \mathscr C) \) is a subspace of \( (\R, \mathscr R) \). Moreover, \( (\R, \mathscr R, \lambda) \) is \( \sigma \)-finite but \( (\R, \mathscr C, \lambda) \) is not.
Proof
If \( x \in \R \), then the singleton \( \{x\} \) is closed and hence is in \( \mathscr R \). A countable set is a countable union of singletons, so if \( A \) is countable then \( A \in \mathscr R \). It follows that \( \mathscr C \subset \mathscr R \). Next, let \( I_n \) denote the interval \( [n, n + 1) \) for \( n \in \Z \). Then \( \lambda(I_n) = 1 \) for \( n \in Z \) and \( \R = \bigcup_{n \in \Z} I_n \), so \( (\R, \mathscr R, \lambda) \) is \( \sigma \)-finite. On the other hand, \( \lambda\{x\} = 0 \) for \( x \in R \) (since the set is an interval of length 0). Therefore \( \lambda(A) = 0 \) if \( A \) is countable and \( \lambda(A) = \infty \) if \( A^c \) is countable. It follows that \( \R \) cannot be written as a countable union of sets in \( \mathscr C \), each with finite measure.
A sum of finite measures may not be \( \sigma \)-finite.
Let \( S \) be a nonempty, finite set with the \( \sigma \)-algebra \( \mathscr S \) of all subsets. Let \( \mu_n = \# \) be counting measure on \( (S, \mathscr S) \) for \( n \in \N_+ \). Then \( \mu_n \) is a finite measure for each \( n \in \N_+ \), but \( \mu = \sum_{n \in \N_+} \mu_n \) is not \( \sigma \)-finite.
Proof
Note that \( \mu \) is the trivial measure on \( (S, \mathscr S) \) given by \( \mu(A) = \infty \) if \( A \ne \emptyset \) (and of course \( \mu(\emptyset) = 0 \)).
Basic Properties
In the following problems, \( \mu \) is a positive measure on the measurable space \( (S, \mathscr S) \).
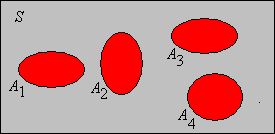
Suppose that \( \mu(S) = 20 \) and that \(A, B \in \mathscr S\) with \(\mu(A) = 5\), \(\mu(B) = 6 \), \(\mu(A \cap B) = 2\). Find the measure of each of the following sets:
- \(A \setminus B\)
- \(A \cup B\)
- \(A^c \cup B^c\)
- \(A^c \cap B^c\)
- \(A \cup B^c\)
Answer
- 3
- 9
- 18
- 11
- 16
Suppose that \( \mu(S) = \infty \) and that \(A, \, B \in \mathscr S\) with \(\mu(A \setminus B) = 2\), \(\mu(B \setminus A) = 3\), and \(\mu(A \cap B) = 4\). Find the measure of each of the following sets:
- \(A\)
- \(B\)
- \(A \cup B\)
- \( A^c \cap B^c \)
- \( A^c \cup B^c \)
Answer
- 6
- 7
- 9
- \(\infty\)
- \(\infty\)
Suppose that \( \mu(S) = 10 \) and that \(A, \, B \in \mathscr S\) with \(\mu(A) = 3\), \(\mu(A \cup B) = 7\), and \(\mu(A \cap B) = 2\). Find the measure of each of the following events:
- \(B\)
- \(A \setminus B\)
- \(B \setminus A\)
- \(A^c \cup B^c\)
- \(A^c \cap B^c\)
Answer
- 6
- 1
- 4
- 8
- 3
Suppose that \( A, \, B, \, C \in \mathscr S \) with \( \mu(A) = 10 \), \( \mu(B) = 12 \), \( \mu(C) = 15 \), \( \mu(A \cap B) = 3 \), \( \mu(A \cap C) = 4 \), \( \mu(B \cap C) = 5 \), and \( \mu(A \cap B \cap C) = 1S \). Find the probabilities of the various unions:
- \( A \cup B \)
- \( A \cup C \)
- \( B \cup C \)
- \( A \cup B \cup C \)
Answer
- 21
- 23
- 22
- 28


