4.2: MATLAB and Independent Classes
- Page ID
- 10868
MATLAB and Independent Classes
In the unit on Minterms, we show how to use minterm probabilities and minterm vectors to calculate probabilities of Boolean combinations of events. In Independence of Events we show that in the independent case, we may calculate all minterm probabilities from the probabilities of the basic events. While these calculations are straightforward, they may be tedious and subject to errors. Fortunately, in this case we have an m-function minprob which calculates all minterm probabilities from the probabilities of the basic or generating sets. This function uses the m-function mintable to set up the patterns of \(p\)'s and \(q\)'s for the various minterms and then takes the products to obtain the set of minterm probabilities.
Example \(\PageIndex{1}\)
>> pm = minprob(0.1*[4 7 6]) pm = 0.0720 0.1080 0.1680 0.2520 0.0480 0.0720 0.1120 0.1680
It may be desirable to arrange these as on a minterm map. For this we have an m-function minmap which reshapes the row matrix \(pm\), as follows:
>> t = minmap(pm)
t = 0.0720 0.1680 0.0480 0.1120
0.1080 0.2520 0.0720 0.1680
Probability of occurrence of k of n independent events
In Example 2, we show how to use the m-functions mintable and csort to obtain the probability of the occurrence of \(k\) of \(n\) events, when minterm probabilities are available. In the case of an independent class, the minterm probabilities are calculated easily by minprob, It is only necessary to specify the probabilities for the \(n\) basic events and the numbers \(k\) of events. The size of the class, hence the mintable, is determined, and the minterm probabilities are calculated by minprob. We have two useful m-functions. If \(P\) is a matrix of the \(n\) individual event probabilities, and \(k\) is a matrix of integers less than or equal to \(n\), then
function \(y = \text{ikn}(P, k)\) calculates individual probabilities that \(k\) of \(n\) occur
function \(y = \text{ckn}(P, k)\) calculates the probabilities that \(k\) or more occur
Example \(\PageIndex{2}\)
>> p = 0.01*[13 37 12 56 33 71 22 43 57 31]; >> k = [2 5 7]; >> P = ikn(p,k) P = 0.1401 0.1845 0.0225 % individual probabilities >> Pc = ckn(p,k) Pc = 0.9516 0.2921 0.0266 % cumulative probabilities
Reliability of systems with independent components
Suppose a system has \(n\) components which fail independently. Let \(E_i\) be the event the \(i\)th component survives the designated time period. Then \(R_i = P(E_i)\) is defined to be the reliability of that component. The reliability \(R\) of the complete system is a function of the component reliabilities. There are three basic configurations. General systems may be decomposed into subsystems of these types. The subsystems become components in the larger configuration. The three fundamental configurations are:
Series. The system operates iff all n components operate: \(R = \prod_{i = 1}^n R_i\)
Parallel. The system operates iff not all components fail: \(R = 1 - \prod_{i = 1}^{n} (1 - R_i)\)
k of n. The system operates iff \(k\) or more components operate. \(R\) may be calculated with the m-function ckn. If the component probabilities are all the same, it is more efficient to use the m-function cbinom (see Bernoulli trials and the binomial distribution, below).
MATLAB solution. Put the component reliabilities in matrix \(RC = [R_1\ R_2\ \cdot\cdot\cdot \ R_n]\)
Series Configuration
>> R = prod(RC) % prod is a built in MATLAB function
Parallel Configuration
>> R = parallel(RC) % parallel is a user defined function
k of n Configuration
>> R = ckn(RC,k) % ckn is a user defined function (in file ckn.m).
Example \(\PageIndex{3}\)
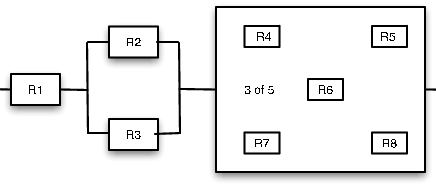
There are eight components, numbered 1 through 8. Component 1 is in series with a parallel combination of components 2 and 3, followed by a 3 of 5 combination of components 4 through 8 (see Figure 1 for a schematic representation). Probabilities of the components in order are
0.95 0.90 0.92 0.80 0.83 0.91 0.85 0.85
The second and third probabilities are for the parallel pair, and the last five probabilities are for the 3 of 5 combination.
>> RC = 0.01*[95 90 92 80 83 91 85 85]; % Component reliabilities >> Ra = RC(1)*parallel(RC(2:3))*ckn(RC(4:8),3) % Solution Ra = 0.9172
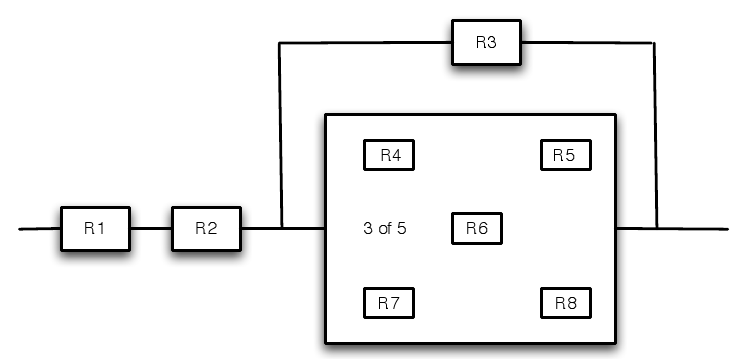
Example \(\PageIndex{4}\)
>> RC = 0.01*[95 90 92 80 83 91 85 85]; % Component reliabilities 1--8 >> Rb = prod(RC(1:2))*parallel([RC(3),ckn(RC(4:8),3)]) % Solution Rb = 0.8532
A test for independence
It is difficult to look at a list of minterm probabilities and determine whether or not the generating events form an independent class. The m-function imintest has as argument a vector of minterm probabilities. It checks for feasible size, determines the number of variables, and performs a check for independence.
Example \(\PageIndex{5}\)
>> pm = 0.01*[15 5 2 18 25 5 18 12]; % An arbitrary class
>> disp(imintest(pm))
The class is NOT independent
Minterms for which the product rule fails
1 1 1 0
1 1 1 0
Example \(\PageIndex{6}\)
>> pm = [0.10 0.15 0.20 0.25 0.30]: %An improper number of probabilities >> disp(imintest(pm)) The number of minterm probabilities incorrect
Example \(\PageIndex{7}\)
>> pm = minprob([0.5 0.3 0.7]); >> disp(imintest(pm)) The class is independent
Probabilities of Boolean combinations
As in the nonindependent case, we may utilize the minterm expansion and the minterm probabilities to calculate the probabilities of Boolean combinations of events. However, it is frequently more efficient to manipulate the expressions for the Boolean combination to be a disjoint union of intersections.
Example \(\PageIndex{8}\) A simple Boolean combination
Suppose the class {\(A\), \(B\), \(C\)} is independent, with respective probabilities 0.4, 0.6, 0.8. Determine \(P(A \cup BC)\). The minterm expansion is
\(A \cup BC = M(3, 4, 5, 6, 7)\), so that \(P(A \cup BC) = p(3, 4, 5, 6, 7)\)
It is not difficult to use the product rule and the replacement theorem to calculate the needed minterm probabilities. Thus \(p(3) = P(A^c) P(B) = P(C) = 0.6 \cdot 0.6 \cdot 0.8 = 0.2280\). Similarly \(p(4) = 0.0320\), \(p(5) = 0.1280\), \(p(6) = 0.0480\), \(p(7) = 0.1920\). The desired probability is the sum of these, 0.6880.
As an alternate approach, we write
\(A \cup BC = A \bigvee A^c BC\), so that \(P(A \cup BC) = 0.4 + 0.6 \cdot 0.6 \cdot 0.8 = 0.6880\)
Considerbly fewer arithmetic operations are required in this calculation.
In larger problems, or in situations where probabilities of several Boolean combinations are to be determined, it may be desirable to calculate all minterm probabilities then use the minterm vector techniques introduced earlier to calculate probabilities for various Boolean combinations. As a larger example for which computational aid is highly desirable, consider again the class and the probabilities utilized in Example 4.2.2, above.
Example \(\PageIndex{9}\)
Consider again the independent class {\(E_1, E_2, \cdot\cdot\cdot E_{10}\)} with respective probabilities [0.13 0.37 0.12 0.56 0.33 0.71 0.22 0.43 0.57 0.31]. We wish to calculateThere are \(2^{10} = 1024\) minterm probabilities to be calculated. Each requires the multiplication of ten numbers. The solution with MATLAB is easy, as follows:
>> P = 0.01*[13 37 12 56 33 71 22 43 57 31]; >> minvec10 Vectors are A1 thru A10 and A1c thru A10c They may be renamed, if desired. >> F = (A1|(A3&(A4|A7c)))|(A2&(A5c|(A6&A8)))|(A9&A10c); >> pm = minprob(P); >> PF = F*pm' PF = 0.6636
Writing out the expression for \(F\) is tedious and error prone. We could simplify as follows:
>> A = A1|(A3&(A4|A7c)); >> B = A2&(A5c|(A6&A8)); >> C = A9&A10c; >> F = A|B|C; % This minterm vector is the same as for F above
This decomposition of the problem indicates that it may be solved as a series of smaller problems. First, we need some central facts about independence of Boolean combinations.
Independent Boolean combinations
Suppose we have a Boolean combination of the events in the class {\(A_i: 1 \le i \le n\)} and a second combination the events in the class {\(B_j: 1 \le j \le m\)}. If the combined class {\(A_i, B_j: 1 \le i \le n, 1 \le j \le m\)} is independent, we would expect the combinations of the subclasses to be independent. It is important to see that this is in fact a consequence of the product rule, for it is further evidence that the product rule has captured the essence of the intuitive notion of independence. In the following discussion, we exhibit the essential structure which provides the basis for the following general proposition.
Proposition. Consider \(n\) distinct subclasses of an independent class of events. If for each \(i\) the event \(A_i) is a Boolean (logical) combination of members of the \(i\)th subclass, then the class {\(A_1, A_2, \cdot\cdot\cdot, A_n} is an independent class.
Verification of this far reaching result rests on the minterm expansion and two elementary facts about the disjoint subclasses of an independent class. We state these facts and consider in each case an example which exhibits the essential structure. Formulation of the general result, in each case, is simply a matter of careful use of notation.
A class each of whose members is a minterm formed by members of a distinct subclass of an independent class is itself an independent class.
Example \(\PageIndex{10}\)
Consider the independent class {\(A_1, A_2, A_3, B_1, B_2, B_3, B_4\)}, with respective probabilities 0.4, 0.7, 0.3, 0.5, 0.8, 0.3, 0.6. Consider \(M_3\), minterm three for the class {\(A_1, A_2, A_3\)}, and \(N_5\), minterm five for the class {\(B_1\), \(B_2\), \(B_3\), \(B_4\)}. Then
\(P(M_3) = P(A_1^c A_2 A_3) = 0.6 \cdot 0.7 \cdot 0.3 = 0.126\) and \(P(N_5) = P(B_1^c B_2 B_3^c B_4) = 0.5 \cdot 0.8 \cdot 0.7 \cdot 0.6 = 0.168\)
Also
\(P(M_3 N_5) = P(A_1^c A_2 A_3 B_1^c B_2 B_3^c B_40 = 0.6 \cdot 0.7 \cdot 0.3 \cdot 0.5 \cdot 0.8 \cdot 0.7 \cdot 0.6\)
\(=(0.6 \cdot 0.7 \cdot 0.3) \cdot (0.5 \cdot 0.8 \cdot 0.7 \cdot 0.6) = P(M_3)P(N_5) = 0.0212\)
The product rule shows the desired independence.
Again, it should be apparent that the result holds for any number of \(A_i\) and \(B_j\); and it can be extended to any number of distinct subclasses of an independent class.
Suppose each member of a class can be expressed as a disjoint union. If each auxiliary class formed by taking one member from each of the disjoint unions is an independent class, then the original class is independent.
Example \(\PageIndex{11}\)
Suppose \(A = A_1 \bigvee A_2 \bigvee A_3\) and \(B = B_1 \bigvee B_2\), with {\(A_i\), \(A_j\)} independent for each pair \(i, j\). SupposeWe wish to show that the pair {\(A\), \(B\)} is independent; i.e., the product rule \(P(AB) = P(A)P(B)\) holds.
COMPUTATION
\(P(A) = P(A_1) + P(A_2) + P(A_3) = 0.3 + 0.4 + 0.1 = 0.8\) and \(P(B) = P(B_1) + P(B_2) = 0.2 + 0.5 = 0.7\)
Now
\(AB = (A_1 \bigvee A_2 \bigvee A_3) (B_1 \bigvee B_2) = A_1B_1 \bigvee A_1 B_2 \bigvee A_2 B_1 \bigvee A_2 B_2 \bigvee A_3 B_1 \bigvee A_3 B_2\)
By additivity and pairwise independence, we have
\(P(AB) = P(A_1) P(B_1) + P(A_1) P(B_2) + P(A_2) P(B_1) + P(A_2)P(B_2) + P(A_3) P(B_1) + P(A_3) P(B_2)\)
\(= 0.3 \cdot 0.2 + 0.3 \cdot 0.5 + 0.4 \cdot 0.2 + 0.4 \cdot 0.5 + 0.1 \cdot 0.2 + 0.1 \cdot 0.5 = 0.56 = P(A) P(B)\)
The product rule can also be established algebraically from the expression for \(P(AB)\), as follows:
\(P(AB) = P(A_1)[P(B_1) + P(B_2)] + P(A_2) [P(B_1) + P(B_2)] + P(A_3) [P(B_1) + P(B_2)]\)
\(= [P(A_1) + P(A_2) + P(A_3)][P(B_1) + P(B_2)] = P(A) P(B)\)
It should be clear that the pattern just illustrated can be extended to the general case. If
then the pair {\(A, B\)} is independent. Also, we may extend this rule to the triple {\(A, B, C\)}
and similarly for any finite number of such combinations, so that the second proposition holds.
Begin with an independent class  of \(n\) events. Select \(m\) distinct subclasses and form Boolean combinations for each of these. Use of the minterm expansion for each of these Boolean combinations and the two propositions just illustrated shows that the class of Boolean combinations is independent
of \(n\) events. Select \(m\) distinct subclasses and form Boolean combinations for each of these. Use of the minterm expansion for each of these Boolean combinations and the two propositions just illustrated shows that the class of Boolean combinations is independent
To illustrate, we return to Example 4.2.9, which involves an independent class of ten events.
Example \(\PageIndex{12}\) A hybrid approach
Consider again the independent class {\(E_1, E_2, \cdot\cdot\cdot, E_{10}\)} with respective probabilities {0.13 0.37 0.12 0.56 0.33 0.71 0.22 0.43 0.57 0.31}. We wish to calculate\(P(F) = P(E_1 \cup E_3 (E_4 \cup E_7^c) \cup E_2 (E_5^c \cup E_6 E_8) \cup E_9 E_10^c)\)
In the previous solution, we use minprob to calculate the \(2^{10}=1024\) minterms for all ten of the \(E_i\) and determine the minterm vector for \(F\). As we note in the alternate expansion of \(F\),
We may calculate directly \(P(C) = 0.57 \cdot 0.69 = 0.3933\). Now \(A\) is a Boolean combination of {\(E_1, E_3, E_4, E_7\)} and B is a combination of {\(E_2, E_5, E_6 E_8\)}. By the result on independence of Boolean combinations, the class {\(A, B, C\)} is independent. We use the m-procedures to calculate \(P(A)\) and \(P(B)\). Then we deal with the independent class {\(A, B, C\)} to obtain the probability of \(F\).
>> p = 0.01*[13 37 12 56 33 71 22 43 57 31];
>> pa = p([1 3 4 7]); % Selection of probabilities for A
>> pb = p([2 5 6 8]); % Selection of probabilities for B
>> pma = minprob(pa); % Minterm probabilities for calculating P(A)
>> pmb = minprob(pb); % Minterm probabilities for calculating P(B)
>> minvec4;
>> a = A|(B&(C|Dc)); % A corresponds to E1, B to E3, C to E4, D to E7
>> PA = a*pma'
PA = 0.2243
>> b = A&(Bc|(C&D)); % A corresponds to E2, B to E5, C to E6, D to E8
>> PB = b*pmb'
PB = 0.2852
>> PC = p(9)*(1 - p(10))
PC = 0.3933
>> pm = minprob([PA PB PC]);
>> minvec3 % The problem becomes a three variable problem
>> F = A|B|C; % with {A,B,C} an independent class
>> PF = F*pm'
PF = 0.6636 % Agrees with the result of Example 4.2.7


