3.E: Examining the Evidence using Graphs and Statistics (Exercises)
- Page ID
- 5453
- Fans of professional sports teams expect the owners of the team to spend the necessary money to get the players who will help them win a championship. The payrolls of various professional sports teams in the US were divided into thirds, and the number of championships won by teams in each third was compared. Make a complete bar graph of this data. (data from unpublished student statistics class project)
Payroll Ranking Number of Championships Lowest Third 2 Middle Third 7 Highest Third 11 - According to National Geographic, in 1903 there were 307 varieties of corn seed sold by seed houses. In 1983, there were 12 varieties sold be seed houses, the rest no longer being used. Find the sample proportion of varieties of corn seed that was still available in 1983 compared to 1903. Make a complete pie chart. (ngm.nationalgeographic.com/20...ariety-graphic viewed 9/9/13)
Do you think it is good or bad that there are fewer varieties? Why? - Between 2010 and 2014, two dams on the Elwha River in the Olympic National Park near Port Angeles, WA were removed, allowing salmon to spawn for the first time in that river in 100 years. Assume the weights of 10 Chinook salmon that returned were recorded. These weights are shown in the table below.
41 48 40 43 45 39 35 47 41 51 The purpose of this problem is to find all the statistics using the formulas by hand. Calculators should only be used to find the square root. Show all work.
Find the mean, variance and standard deviation, and the 5 box plot numbers for this data.
- Students in development mental math classes such as intermediate algebra are expected to know their math facts quickly. Automaticity, or math fact fluency, is the ability to recall math facts without having to make the calculations. The benefit of quickly knowing the math facts is that the working memory of the brain is not filled with the effort to make the calculations so that it can focus on the higher level thinking required for the algebra. Intermediate algebra students were given an automaticity test in which they had to solve as many one-step linear equations as possible in one minute. All addition, subtraction and multiplication equations used numbers between –10 and 10 while division equations had answers in that range. All answers were integers. The table below gives the number of problems completed successfully in one minute.
11 30 28 31 23 27 29 9 38 18 19 17 26 12 10 19 20 17 15 23 22 34 23 36 10 Make a frequency distribution and histogram. Using a starting value of 5 and a class width of 5. Label the graph completely.
Make a box plot. - The objective of the automaticity experiments is to determine if there is a relationship between a student’s math fact fluency and their final grade for the quarter. The table below contains the bivariate data for 6 of the students.
Automaticity Score Final Grade Student 1 19 4 Student 2 31 2.9 Student 3 16 1.4 Student 4 19 4 Student 5 20 2.3 Student 6 16 1.3 Make a scatter plot for this data.
Find the correlation using the formulas. You can use your calculator for the basic functions but not for simply finding correlation, other than to check your answer. Show all your work. - Automaticity is one area to investigate when a college attempts to improve success rates for developmental math classes. If it is a factor in success, then the college will develop a method for helping students improve their automaticity. An experiment was conducted in which intermediate algebra students were given a computerized automaticity test that required them to solve a mixture of one-step linear equations that required adding, subtracting or multiplying numbers between -10 and 10 and has solutions between those same values for the division problems. Examples include -3x = 12 and x + 5 = -3. A student’s score was the maximum number of problems they could answer correctly in one minute. Students had to get an answer correct before moving on to a new problem. One goal was to see if the average number of problems answered correctly in one minute was greater for students who passed the class than for those who didn’t pass.
The hypotheses that will be tested are:
\(H_0: \mu_\text{pass} = \mu_{fall}\)
\(H_0: \mu_\text{pass} > \mu_{fall}\)
\(\alpha = 0.05\)
a. Complete the design layout table.Research Design Table Research Question: Type of Research Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response varialbe? What is the parameter that will be calculated? Mean Proportion Correlation List potential latent variables. Grouping/explanatory Variable 1 (if present) Levels:
b. If two intermediate algebra classes were to be randomly selected from 12 classes being offered, with the classes being numbered 1 to 12, which two classes would be selected if the calculator was seeded with 27 or row 10 was used in the table of random digits?
c. What type of sampling method is used when a class is selected and everyone in the class participates in the research?
d. The data that will be gathered is the number of problems answered correctly in one minute. Are these data quantitative discrete, quantitative continuous or categorical?
The automaticity scores for the students who failed the class are shown in the table below.16 15 14 15 13 16 22 30 20 8 13 14 16 16 16 16 6 27 9 The automaticity scores for the students who passed the class are shown in the table below.
20 19 33 15 20 14 9 11 12 17 8 20 31 38 29 9 22 31 31 30 9 22 31 31 30 15 10 10 23 22 7 11 23 17 19 20 20 18 9 27 25 15 18 9 27 25 15 23 28 11 20 13 36 34 e. Make a frequency distribution, double bar histogram and side-by-side box plots to show a graphical comparison of these two sets of scores.
f. Which graph is more effective in helping you see the difference between the data sets?
g. Find the mean, variance and standard deviation for both sets of data separately. You may use the statistical functions of your calculator.
h. The p-value of the statistical test that compares the two means is 0.0395. Write a concluding sentence in the style used in scholarly journals (like you were taught in Chapter 1).
i. Based on the results of this analysis and the decision rule in the story, will the college develop a program to help improve automaticity? - Why Statistical Reasoning Is Important for a Biology Student and Professional Developed in collaboration with Elysia Mbuja and Robert Thissen, Biology Department This topic is discussed in BIOL 160, General Biology.
To explore the scientific method, students will study the effect of alcohol on a Daphnia. Daphnia, living water fleas, are used because they are almost transparent and the beating heart can be seen. The theory to be tested is whether alcohol slows the heart rate of Daphnia. To conduct this test, a Daphnia will be placed in a drop of water on a microscope. The number of heartbeats in 15 seconds will be counted. The water will be removed from the slide and a drop of 8% alcohol will be placed on the Daphnia. After 1 minute, the heartbeats will be counted again. If the heartbeats are lower, it cannot be concluded that the reason is because of the alcohol. It could simply be the reaction to a drop of fluid being placed on the Daphnia or the effect of being on a slide under a light. Therefore, after the Daphnia is allowed to recover, it is returned to the slide following the exact same procedure except a drop of water is used instead of alcohol.
\(H_0: \mu_{\text{alcohol}} = \mu_{\text{water}}\)
\(H_1: \mu_{\text{alcohol}} < \mu_{\text{water}}\)
\(\alpha = 0.05\)
a. Complete the experiment design table.Research Design Table Research Question: Type of Research Observational Study
Observational Experiment
Manipulative ExperimentWhat is the response varialbe? What is the parameter that will be calculated? Mean Proportion Correlation List potential latent variables. Grouping/explanatory Variable 1 (if present) Levels:
b. Make an appropriate graph to compare the two sets of data. The data in the shaded cells is authentic. It comes from a BIOL 160 class.
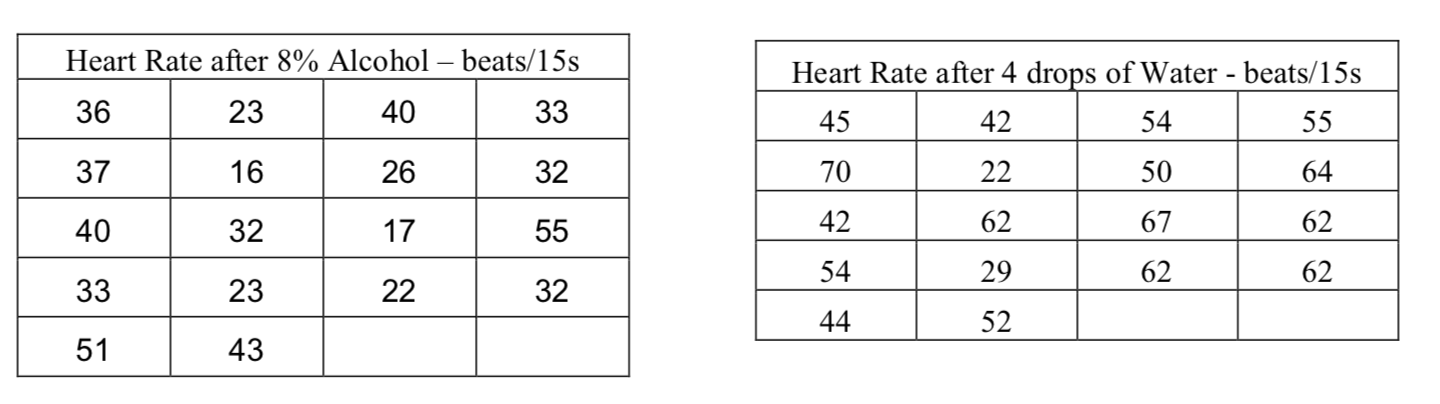
c. Show the relevant statistics for the two sets of data.Heart Rate after Alcohol Heart Rate after Water Mean Standard Deviation Median
d. The p-value from the t-test for 2 independent populations is 1.28E-5. Write a concluding sentence.
e. What is the effect of alcohol on the heart rate of a Daphnia? Do you think it will have the same effect on a human?


