32.3: The Reproducibility Crisis in Science
- Page ID
- 8878
While we think that the kind of frauduent behavior seen in Wansink’s case is relatively rare, it has become increasingly clear that problems with reproducibility are much more widespread in science than previously thought. This became clear in 2015, when a large group of researchers published a study in the journal Science titled “Estimating the reproducibility of psychological science”(Open Science Collaboration 2015). In this study, the researchers took 100 published studies in psychology and attempted to reproduce the results originally reported in the papers. Their findings were shocking: Whereas 97% of the original papers had reported statistically significant findings, only 37% of these effects were statistically significant in the replication study. Although these problems in psychology have received a great deal of attention, they seem to be present in nearly every area of science, from cancer biology (Errington et al. 2014) and chemistry (Baker 2017) to economics (Christensen and Miguel 2016) and the social sciences (Camerer et al. 2018).
The reproducibility crisis that emerged after 2010 was actually predicted by John Ioannidis, a physician from Stanford who wrote a paper in 2005 titled “Why most published research findings are false”(Ioannidis 2005). In this article, Ioannidis argued that the use of null hypothesis statistical testing in the context of modern science will necessarily lead to high levels of false results.
32.3.1 Positive predictive value and statistical significance
Ioannidis’ analysis focused on a concept known as the positive predictive value, which is defined as the proportion of positive results (which generally translates to “statistically significant findings”) that are true:
Assuming that we know the probability that our hypothesis is true (), then the probability of a true positive result is simply multiplied by the statistical power of the study:
were is the false negative rate. The probability of a false positive result is determined by and the false positive rate :
PPV is then defined as:
Let’s first take an example where the probability of our hypothesis being true is high, say 0.8 - though note that in general we cannot actually know this probability. Let’s say that we perform a study with the standard values of and . We can compute the PPV as:
This means that if we find a positive result in a study where the hypothesis is likely to be true and power is high, then its likelihood of being true is high. Note, however, that a research field where the hypotheses have such a high likelihood of being true is probably not a very interesting field of research; research is most important when it tells us something new!
Let’s do the same analysis for a field where – that is, most of the hypotheses being tested are false. In this case, PPV is:
This means that in a field where most of the hypotheses are likely to be wrong (that is, an interesting scientific field where researchers are testing risky hypotheses), even when we find a positive result it is more likely to be false than true! In fact, this is just another example of the base rate effect that we discussed in the context of hypothesis testing – when an outcome is unlikely, then it’s almost certain that most positive outcomes will be false positives.
We can simulate this to show how PPV relates to statistical power, as a function of the prior probability of the hypothesis being true (see Figure 32.1)
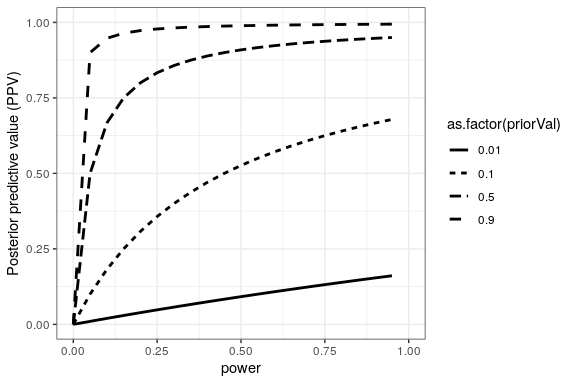
Unfortunately, statistical power remains low in many areas of science (Smaldino and McElreath 2016), suggesting that many published research findings are false.
An amusing example of this was seen in a paper by Jonathan Schoenfeld and John Ioannidis, titled “Is everything we eat associated with cancer? A systematic cookbook review”[scho:ioan:2013]. They examined a large number of papers that had assessed the relation between different foods and cancer risk, and found that 80% of ingredients had been associated with either increased or decreased cancer risk. In most of these cases, the statistical evidence was weak, and when the results were combined across studies, the result was null.
32.3.2 The winner’s curse
Another kind of error can also occur when statistical power is low: Our estimates of the effect size will be inflated. This phenomenon often goes by the term “winner’s curse”, which comes from economics, where it refers to the fact that for certain types of auctions (where the value is the same for everyone, like a jar of quarters, and the bids are private), the winner is guaranteed to pay more than the good is worth. In science, the winner’s curse refers to the fact that the effect size estimated from a significant result (i.e. a winner) is almost always an overestimate of the true effect size.
We can simulate this in order to see how the estimated effect size for significant results is related to the actual underlying effect size. Let’s generate data for which there is a true effect size of 0.2, and estimate the effect size for those results where there is a significant effect detected. The left panel of Figure 32.2 shows that when power is low, the estimated effect size for significant results can be highly inflated compared to the actual effect size.

We can look at a single simulation to see why this is the case. In the right panel of Figure 32.2, you can see a histogram of the estimated effect sizes for 1000 samples, separated by whether the test was statistically significant. It should be clear from the figure that if we estimate the effect size only based on significant results, then our estimate will be inflated; only when most results are significant (i.e. power is high and the effect is relatively large) will our estimate come near the actual effect size.


