26.6: What Does “Predict” Really Mean?
- Page ID
- 8855
When we talk about “prediction” in daily life, we are generally referring to the ability to estimate the value of some variable in advance of seeing the data. However, the term is often used in the context of linear regression to refer to the fitting of a model to the data; the estimated values (
As an example, let’s take a sample of 48 children from NHANES and fit a regression model for weight that includes several regressors (age, height, hours spent watching TV and using the computer, and household income) along with their interactions.
| Data type | RMSE (original data) | RMSE (new data) |
|---|---|---|
| True data | 3.0 | 21 |
| Shuffled data | 7.6 | 59 |
Here we see that whereas the model fit on the original data showed a very good fit (only off by a few pounds per individual), the same model does a much worse job of predicting the weight values for new children sampled from the same population (off by more than 25 pounds per individual). This happens because the model that we specified is quite complex, since it includes not just each of the individual variables, but also all possible combinations of them (i.e. their interactions), resulting in a model with 32 parameters. Since this is almost as many coefficients as there are data points (i.e., the heights of 48 children), the model overfits the data, just like the complex polynomial curve in our initial example of overfitting in Section 8.4.
Another way to see the effects of overfitting is to look at what happens if we randomly shuffle the values of the weight variable (shown in the second row of the table). Randomly shuffling the value should make it impossible to predict weight from the other variables, because they should have no systematic relationship. This shows us that even when there is no true relationship to be modeled (because shuffling should have obliterated the relationship), the complex model still shows a very low error in its predictions, because it fits the noise in the specific dataset. However, when that model is applied to a new dataset, we see that the error is much larger, as it should be.
26.6.1 Cross-validation
One method that has been developed to help address the problem of overfitting is known as cross-validation. This technique is commonly used within the field of machine learning, which is focused on building models that will generalize well to new data, even when we don’t have a new dataset to test the model. The idea behind cross-validation is that we fit our model repeatedly, each time leaving out a subset of the data, and then test the ability of the model to predict the values in each held-out subset.
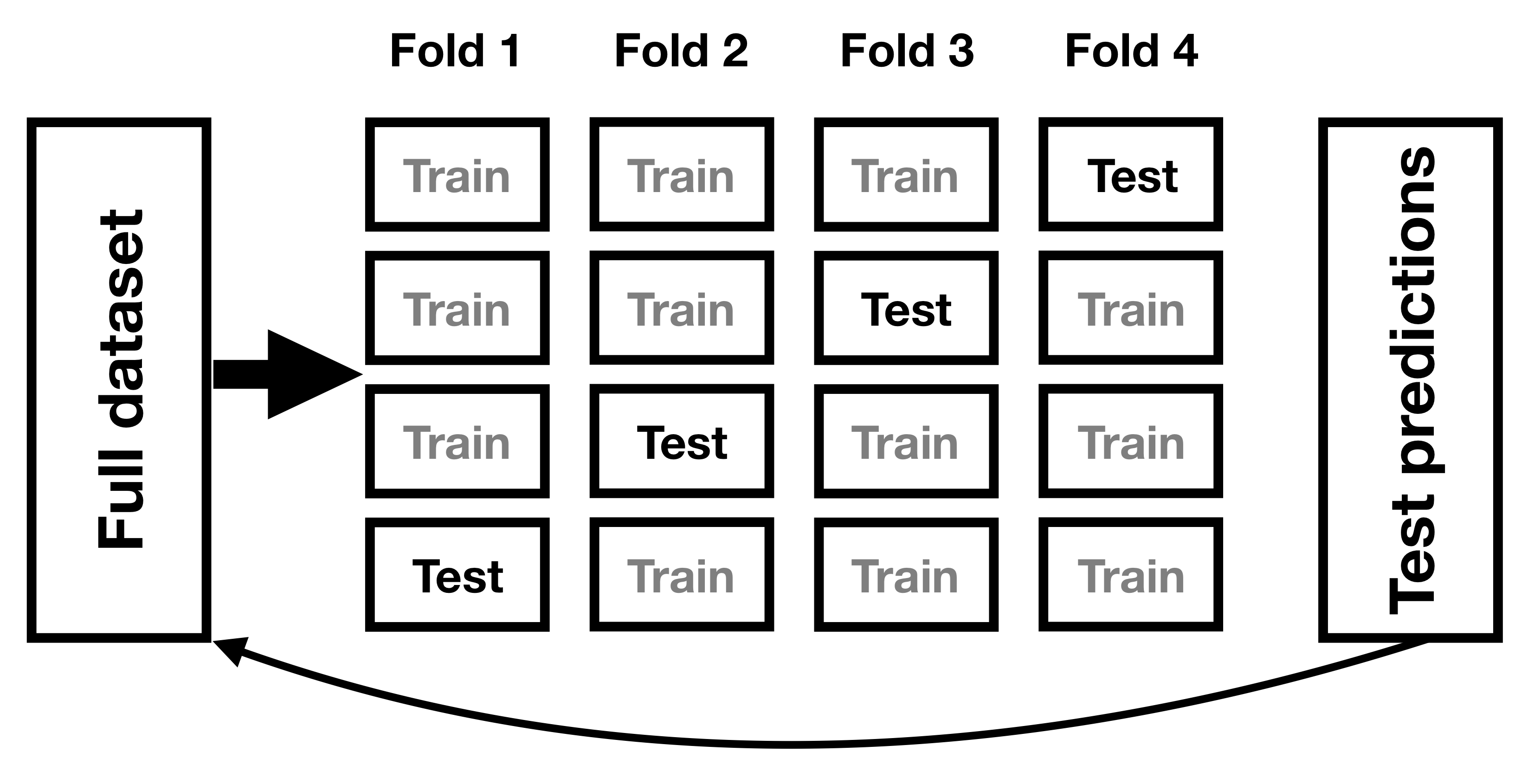
Let’s see how that would work for our weight prediction example. In this case we will perform 12-fold cross-validation, which means that we will break the data into 12 subsets, and then fit the model 12 times, in each case leaving out one of the subsets and then testing the model’s ability to accurately predict the value of the dependent variable for those held-out data points. The caret package in R provides us with the ability to easily run cross-validation across our dataset. Using this function we can run cross-validation on 100 samples from the NHANES dataset, and compute the RMSE for cross-validation, along with the RMSE for the original data and a new dataset, as we computed above.
| Root mean squared error | |
|---|---|
| Original data | 3 |
| New data | 24 |
| Cross-validation | 146 |
Here we see that cross-validation gives us an estimate of predictive accuracy that is much closer to what we see with a completely new dataset than it is to the inflated accuracy that we see with the original dataset – in fact, it’s even slighlty more pessimistic than the average for a new dataset, probably because only part of the data are being used to train each of the models.
Note that using cross-validation properly is tricky, and it is recommended that you consult with an expert before using it in practice. However, this section has hopefully shown you three things:
- “Prediction” doesn’t always mean what you think it means
- Complex models can overfit data very badly, such that one can see seemingly good prediction even when there is no true signal to predict
- You should view claims about prediction accuracy very skeptically unless they have been done using the appropriate methods.


