21.2: Estimating Posterior Distributions (Section 20.4)
- Page ID
- 8830
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
# create a table with results
nResponders <- 64
nTested <- 100
drugDf <- tibble(
outcome = c("improved", "not improved"),
number = c(nResponders, nTested - nResponders)
)Computing likelihood
likeDf <-
tibble(resp = seq(1,99,1)) %>%
mutate(
presp=resp/100,
likelihood5 = dbinom(resp,100,.5),
likelihood7 = dbinom(resp,100,.7),
likelihood3 = dbinom(resp,100,.3)
)
ggplot(likeDf,aes(resp,likelihood5)) +
geom_line() +
xlab('number of responders') + ylab('likelihood') +
geom_vline(xintercept = drugDf$number[1],color='blue') +
geom_line(aes(resp,likelihood7),linetype='dotted') +
geom_line(aes(resp,likelihood3),linetype='dashed')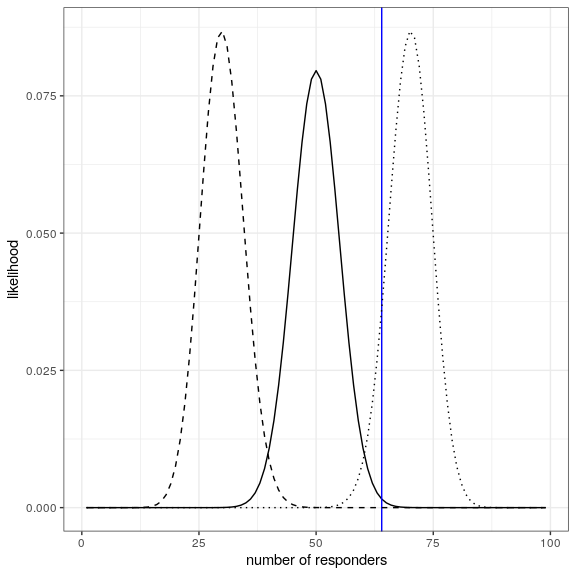
Computing marginal likelihood
# compute marginal likelihood
likeDf <-
likeDf %>%
mutate(uniform_prior = array(1 / n()))
# multiply each likelihood by prior and add them up
marginal_likelihood <-
sum(
dbinom(
x = nResponders, # the number who responded to the drug
size = 100, # the number tested
likeDf$presp # the likelihood of each response
) * likeDf$uniform_prior
)Comuting posterior
bayesDf <-
tibble(
steps = seq(from = 0.01, to = 0.99, by = 0.01)
) %>%
mutate(
likelihoods = dbinom(
x = nResponders,
size = 100,
prob = steps
),
priors = dunif(steps) / length(steps),
posteriors = (likelihoods * priors) / marginal_likelihood
)
# compute MAP estimate
MAP_estimate <-
bayesDf %>%
arrange(desc(posteriors)) %>%
slice(1) %>%
pull(steps)
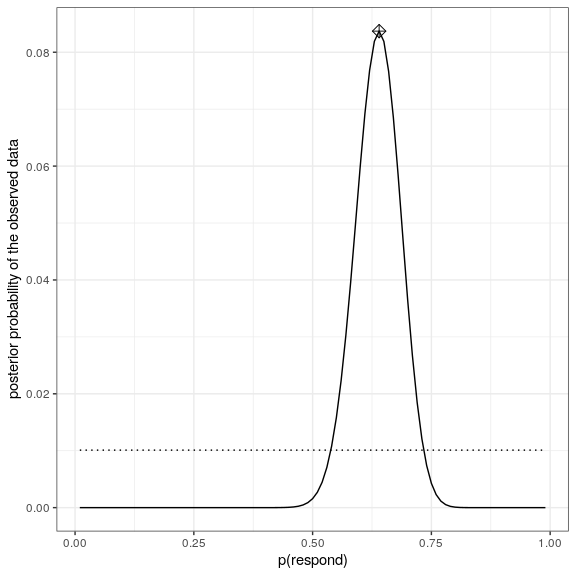
ggplot(bayesDf,aes(steps,posteriors)) +
geom_line() +
geom_line(aes(steps,priors),
color='black',
linetype='dotted') +
xlab('p(respond)') +
ylab('posterior probability of the observed data') +
annotate(
"point",
x = MAP_estimate,
y = max(bayesDf$posteriors),
shape=9,
size = 3
)