18.1: Confidence Intervals
- Page ID
- 8809
So far in the book we have focused on estimating the specific value of a statistic. For example, let’s say we want to estimate the mean weight of adults in the NHANES dataset. Let’s take a sample from the dataset and estimate the mean. In this sample, the mean weight was 79.92 kilograms. We refer to this as a point estimate since it provides us with a single number to describe the difference. However, we know from our earlier discussion of sampling error that there is some uncertainty about this estimate, which is described by the standard error. You should also remember that the standard error is determined by two components: the population standard deviation (which is the numerator), and the square root of the sample size (which is in the denominator). The population standard deviation is an unknown but fixed parameter that is not under our control, whereas the sample size is under our control. Thus, we can decrease our uncertainty about the estimate by increasing our sample size – up to the limit of the entire population size, at which point there is no uncertainty at all because we can just calculate the population parameter directly from the data of the entire population.
You may also remember that earlier we introduced the concept of a confidence interval, which is a way of describing our uncertainty about a statistical estimate. Remember that a confidence interval describes an interval that will on average contain the true population parameter with a given probability; for example, the 95% confidence interval is an interval that will capture the true population parameter 95% of the time. Note again that this is not a statement about the population parameter; any particular confidence interval either does or does not contain the true parameter. As Jerzy Neyman, the inventor of the confidence interval, said:
“The parameter is an unknown constant and no probability statement concerning its value may be made.”(Neyman 1937)
The confidence interval for the mean is computed as:
where the critical value is determined by the sampling distribution of the estimate. The important question, then, is what that sampling distribution is.
18.1.1 Confidence intervals using the normal distribution
If we know the population standard deviation, then we can use the normal distribution to compute a confidence interval. We usually don’t, but for our example of the NHANES dataset we do (it’s 21.3 for weight).
Let’s say that we want to compute a 95% confidence interval for the mean. The critical value would then be the values of the standard normal distribution that capture 95% of the distribution; these are simply the 2.5th percentile and the 97.5th percentile of the distribution, which we can compute using the qnorm() function in R, and come out to . Thus, the confidence interval for the mean () is:
Using the estimated mean from our sample (79.92) and the known population standard deviation, we can compute the confidence interval of [77.28,82.56].
18.1.2 Confidence intervals using the t distribution
As stated above, if we knew the population standard deviation, then we could use the normal distribution to compute our confidence intervals. However, in general we don’t – in which case the t distribution is more appropriate as a sampling distribution. Remember that the t distribution is slightly broader than the normal distribution, especially for smaller samples, which means that the confidence intervals will be slightly wider than they would if we were using the normal distribution. This incorporates the extra uncertainty that arises when we make conclusions based on small samples.
We can compute the 95% confidence interval in a way similar to the normal distribution example above, but the critical value is determined by the 2.5th percentile and the 97.5th percentile of the t distribution, which we can compute using the qt() function in R. Thus, the confidence interval for the mean () is:
where is the critical t value. For the NHANES weight example (with sample size of 250), the confidence interval would be 79.92 +/- 1.97 [77.15 - 82.69].
Remember that this doesn’t tell us anything about the probability of the true population value falling within this interval, since it is a fixed parameter (which we know is 81.77 because we have the entire population in this case) and it either does or does not fall within this specific interval (in this case, it does). Instead, it tells us that in the long run, if we compute the confidence interval using this procedure, 95% of the time that confidence interval will capture the true population parameter.
18.1.3 Confidence intervals and sample size
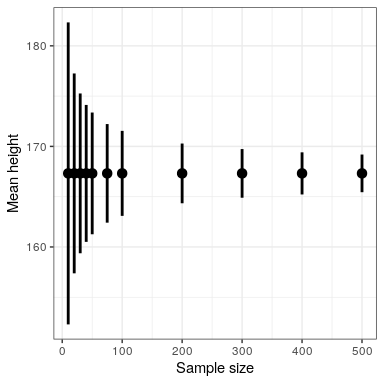
Because the standard error decreases with sample size, the means confidence interval should get narrower as the sample size increases, providing progressively tighter bounds on our estimate. Figure 18.1 shows an example of how the confidence interval would change as a function of sample size for the weight example. From the figure it’s evident that the confidence interval becomes increasingly tighter as the sample size increases, but increasing samples provide diminishing returns, consistent with the fact that the denominator of the confidence interval term is proportional to the square root of the sample size.
18.1.4 Computing confidence intervals using the bootstrap
In some cases we can’t assume normality, or we don’t know the sampling distribution of the statistic. In these cases, we can use the bootstrap (which we introduced in Chapter 14). As a reminder, the bootstrap involves repeatedly resampling the data with replacement, and then using the distribution of the statistic computed on those samples as a surrogate for the sampling distribution of the statistic. R includes a package called boot that we can use to run the bootstrap and compute confidence intervals. It’s always good to use a built-in function to compute a statistic if it is available, rather than coding it up from scratch — both because it saves you extra work, and because the built-in version will be better tested. These are the results when we use the boot() to compute the confidence interval for weight in our NHANES sample:
## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = bs, type = "perc")
##
## Intervals :
## Level Percentile
## 95% (77, 83 )
## Calculations and Intervals on Original ScaleThese values are fairly close to the values obtained using the t distribution above, though not exactly the same.
18.1.5 Relation of confidence intervals to hypothesis tests
There is a close relationship between confidence intervals and hypothesis tests. In particular, if the confidence interval does not include the null hypothesis, then the associated statistical test would be statistically significant. For example, if you are testing whether the mean of a sample is greater than zero with , you could simply check to see whether zero is contained within the 95% confidence interval for the mean.
Things get trickier if we want to compare the means of two conditions (Schenker and Gentleman 2001). There are a couple of situations that are clear. First, if each mean is contained within the confidence interval for the other mean, then there is certainly no significant difference at the chosen confidence level. Second, if there is no overlap between the confidence intervals, then there is certainly a significant difference at the chosen level; in fact, this test is substantially conservative, such that the actual error rate will be lower than the chosen level. But what about the case where the confidence intervals overlap one another but don’t contain the means for the other group? In this case the answer depends on the relative variability of the two variables, and there is no general answer. In general we should avoid using the “visual test” for overlapping confidence intervals.


