13.2: Central Limit Theorem
- Page ID
- 8791
The central limit theorem tells us that the sampling distribution of the mean becomes normal as the sample size grows. Let’s test this by sampling a clearly non-normal variable and look at the normality of the results using a Q-Q plot. We saw in Figure @ref{fig:alcDist50} that the variable AlcoholYear is distributed in a very non-normal way. Let’s first look at the Q-Q plot for these data, to see what it looks like. We will use the stat_qq() function from ggplot2 to create the plot for us.
# prepare the dta
NHANES_cleanAlc <- NHANES %>%
drop_na(AlcoholYear)
ggplot(NHANES_cleanAlc, aes(sample=AlcoholYear)) +
stat_qq() +
# add the line for x=y
stat_qq_line()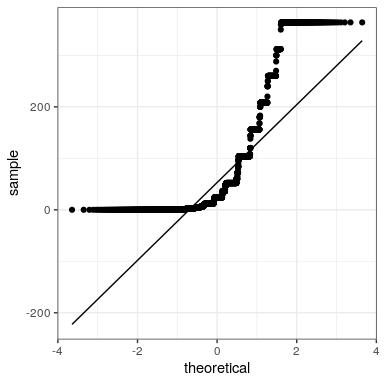
We can see from this figure that the distribution is highly non-normal, as the Q-Q plot diverges substantially from the unit line.
Now let’s repeatedly sample and compute the mean, and look at the resulting Q-Q plot. We will take samples of various sizes to see the effect of sample size. We will use a function from the dplyr package called do(), which can run a large number of analyses at once.
set.seed(12345)
sampSizes <- c(16, 32, 64, 128) # size of sample
nsamps <- 1000 # number of samples we will take
# create the data frame that specifies the analyses
input_df <- tibble(sampSize=rep(sampSizes,nsamps),
id=seq(nsamps*length(sampSizes)))
# create a function that samples and returns the mean
# so that we can loop over it using replicate()
get_sample_mean <- function(sampSize){
meanAlcYear <-
NHANES_cleanAlc %>%
sample_n(sampSize) %>%
summarize(meanAlcoholYear = mean(AlcoholYear)) %>%
pull(meanAlcoholYear)
return(tibble(meanAlcYear = meanAlcYear, sampSize=sampSize))
}
# loop through sample sizes
# we group by id so that each id will be run separately by do()
all_results = input_df %>%
group_by(id) %>%
# "." refers to the data frame being passed in by do()
do(get_sample_mean(.$sampSize))Now let’s create separate Q-Q plots for the different sample sizes.
# create empty list to store plots
qqplots = list()
for (N in sampSizes){
sample_results <-
all_results %>%
filter(sampSize==N)
qqplots[[toString(N)]] <- ggplot(sample_results,
aes(sample=meanAlcYear)) +
stat_qq() +
# add the line for x=y
stat_qq_line(fullrange = TRUE) +
ggtitle(sprintf('N = %d', N)) +
xlim(-4, 4)
}
plot_grid(plotlist = qqplots)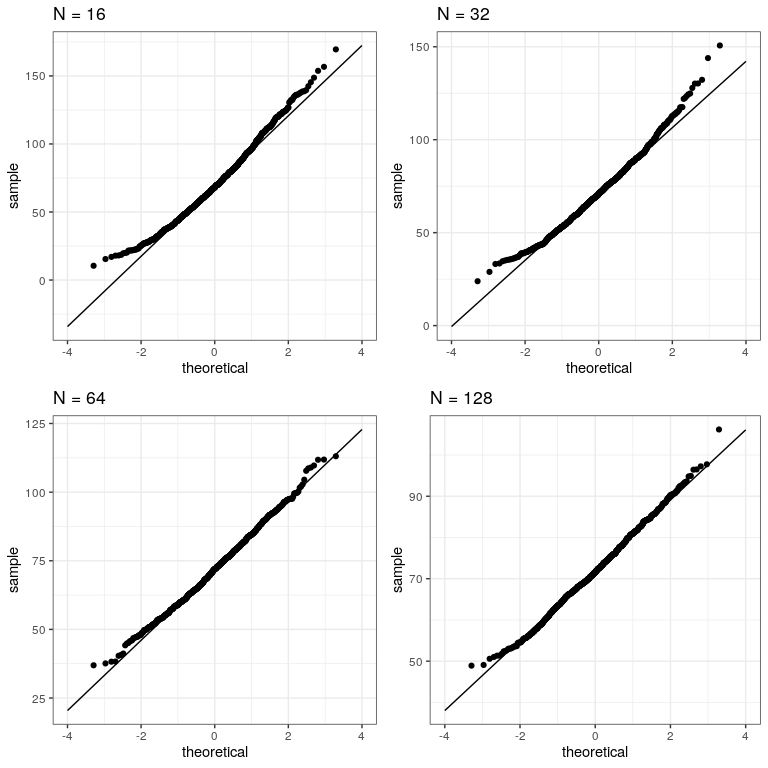
This shows that the results become more normally distributed (i.e. following the straight line) as the samples get larger.


