10.5: How Do We Determine Probabilities?
- Page ID
- 8765
Now that we know what a probability is, how do we actually figure out what the probability is for any particular event?
Let’s say that I asked you what the probability was that the Beatles would have been equally successful if they had not replaced their original drummer Pete Best with Ringo Starr in 1962. We will define “success” in terms of the number of number-one hits on the Billboard Hot 100 (which we refer to as Nhits); the Beatles had 20 such number-one hits, so the sample space is {Nhits<20,Nhits≥20 }. We can’t actually do the experiment to find the outcome. However, most people with knowledge of the Beatles would be willing to at leaste offer a guess at the probability of this event. In many cases personal knowledge and/or opinion is the only guide we have determining the probability of an event, but this is not very scientifically satisfying.
10.2.2 Empirical frequency
Another way to determine the probability of an event is to do the experiment many times and count how often each event happens. From the relative frequency of the different outcomes, we can compute the probability of each. For example, let’s say that we are interested in knowing the probability of rain in San Francisco. We first have to define the experiment — let’s say that we will look at the National Weather Service data for each day in 2017 and determine whether there was any rain at the downtown San Francisco weather station.
| Number of rainy days | Number of days measured | P(rain) |
|---|---|---|
| 73 | 365 | 0.2 |
| According to these data | , in 2017 there were rain | y days. To compute the probability of rain in San Francisco, we simply divide the number of rainy days by the number of days counted (365), giving P(rain in SF in 2017) = . |
How do we know that empirical probability gives us the right number? The answer to this question comes from the law of large numbers, which shows that the empirical probability will approach the true probability as the sample size increases. We can see this by simulating a large number of coin flips, and looking at our estimate of the probability of heads after each flip. We will spend more time discussing simulation in a later chapter; for now, just assume that we have a computational way to generate a random outcome for each coin flip.
The left panel of Figure 10.1 shows that as the number of samples (i.e., coin flip trials) increases, the estimated probability of heads converges onto the true value of 0.5. However, note that the estimates can be very far off from the true value when the sample sizes are small. A real-world example of this was seen in the 2017 special election for the US Senate in Georgia, which pitted the Republican Roy Moore against Democrat Doug Jones. The right panel of Figure 10.1 shows the relative amount of the vote reported for each of the candidates over the course of the evening, as an increasing number of ballots were counted. Early in the evening the vote counts were especially volatile, swinging from a large initial lead for Jones to a long period where Moore had the lead, until finally Jones took the lead to win the race.
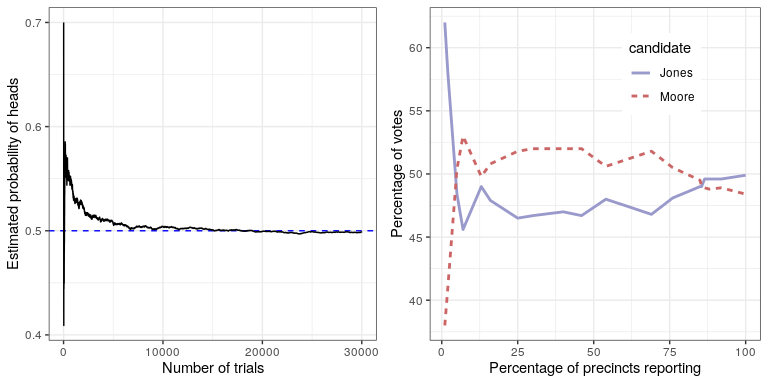
These two examples show that while large samples will ultimately converge on the true probability, the results with small samples can be far off. Unfortunately, many people forget this and overinterpret results from small samples. This was referred to as the law of small numbers by the psychologists Danny Kahneman and Amos Tversky, who showed that people (even trained researchers) often behave as if the law of large numbers applies even to small samples, giving too much credence to results from small datasets. We will see examples throughout the course of just how unstable statistical results can be when they are generated on the basis of small samples.
10.2.3 Classical probability
It’s unlikely that any of us has ever flipped a coin tens of thousands of times, but we are nonetheless willing to believe that the probability of flipping heads is 0.5. This reflects the use of yet another approach to computing probabilities, which we refer to as classical probability. In this approach, we compute the probability directly based on our knowledge of the situation.
Classical probability arose from the study of games of chance such as dice and cards. A famous example arose from a problem encountered by a French gambler who went by the name of Chevalier de Méré. de Méré played two different dice games: In the first he bet on the chance of at least one six on four rolls of a six-sided die, while in the second he bet on the chance of at least one double-six on 24 rolls of two dice. He expected to win money on both of these gambles, but he found that while on average he won money on the first gamble, he actually lost money on average when he played the second gamble many times. To understand this he turned to his friend, the mathematician Blaise Pascal, who is now recognized as one of the founders of probability theory.
How can we understand this question using probability theory? In classical probability, we start with the assumption that all of the elementary events in the sample space are equally likely; that is, when you roll a die, each of the possible outcomes ({1,2,3,4,5,6}) is equally likely to occur. (No loaded dice allowed!) Given this, we can compute the probability of any individual outcome as one divided by the number of possible outcomes:
\(\ P(outcome_i)=\frac{1}{number\ of\ possible\ outcomes}\)
For the six-sided die, the probability of each individual outcome is 1/6.
This is nice, but de Méré was interested in more complex events, like what happens on multiple dice throws. How do we compute the probability of a complex event (which is a union of single events), like rolling a one on the first or the second throw?
We represent the union of events mathematically using the ∪ symbol: for example, if the probability of rolling a one on the first throw is referred to as P(Roll1throw1) and the probability of rolling a one on the second throw is P(Roll1throw2), then the union is referred to as P(Roll1throw1∪Roll1throw2).
de Méré thought (incorrectly, as we will see below) that he could simply add together the probabilities of the individual events to compute the probability of the combined event, meaning that the probability of rolling a one on the first or second roll would be computed as follows:
\(P\left(\text {Roll} 1_{\text {throw1}}\right)=1 / 6\)
\(P\left(\text {Roll} 1_{\text {throw2}}\right)=1 / 6\)
\(\ deMéré ^{\prime}s\ error: \)
\(P\left(\text {Roll } 1_{\text {throw1}} \cup \text {Roll }_{t \text {throw2}}\right)=P\left(\text {Roll } 1_{\text {throw1}}\right)+P\left(\text {Roll } 1_{\text {throw2}}\right)=1 / 6+1 / 6=1 / 3\)
de Méré reasoned based on this that the probability of at least one six in four rolls was the sum of the probabilities on each of the individual throws: \(\ 4 * \frac{1}{6}=\frac{2}{3}\). Similarly, he reasoned that since the probability of a double-six in throws of dice is 1/36, then the probability of at least one double-six on 24 rolls of two dice would be \(\ 24 * \frac{1}{36}=\frac{2}{3}\). Yet, while he consistently won money on the first bet, he lost money on the second bet. What gives?
To understand de Méré’s error, we need to introduce some of the rules of probability theory. The first is the rule of subtraction, which says that the probability of some event A not happening is one minus the probability of the event happening:
P(¬A)=1−P(A)
where ¬A means “not A”. This rule derives directly from the axioms that we discussed above; because A and ¬A are the only possible outcomes, then their total probability must sum to 1. For example, if the probability of rolling a one in a single throw is \(\ \frac{1}{6}\), then the probability of rolling anything other than a one is \(\ \frac{5}{6}\).
A second rule tells us how to compute the probability of a conjoint event – that is, the probability that both of two events will occur. We refer to this as an intersection, which is signified by the ∩ symbol; thus, P(A∩B) means the probability that both A and B will occur.
This version of the rule tells us how to compute this quantity in the special case when the two events are independent from one another; we will learn later exactly what the concept of independence means, but for now we can just take it for granted that the two die throws are independent events. We compute the probability of the union of two independent events by simply multiplying the probabilities of the individual events:
P(A∩B)=P(A)∗P(B) if and only if A and B are independent
Thus, the probability of throwing a six on both of two rolls is \(\ \frac{1}{6} * \frac{1}{6} = \frac{1}{36}\)
The third rule tells us how to add together probabilities - and it is here that we see the source of de Méré’s error. The addition rule tells us that to obtain the probability of either of two events occurring, we add together the individual probabilities, but then subtract the likelihood of both occurring together:
P(A∪B)=P(A)+P(B)−P(A∩B)
In a sense, this prevents us from counting those instances twice, and that’s what distinguishes the rule from de Méré’s incorrect computation. Let’s say that we want to find the probability of rolling 6 on either of two throws. According to our rules:
\(P\left(\text {Roll } 1_{\text {throw1 }} \cup \text { Roll } 1_{\text {throw } 2}\right)=P\left(\text {Roll } 1_{\text {throw1 }}\right)+P\left(\text {Roll } 1_{\text {throw } 2}\right)-P\left(\text {Roll }_{\text {throw } 1} \cap \text {Roll }_{\text {throw } 2}\right)\)
\(\ =\frac{1}{6}+\frac{1}{6}-\frac{1}{36}=\frac{11}{36}
\)
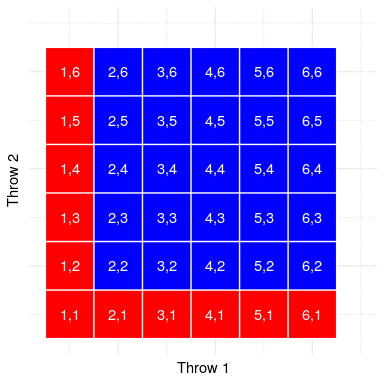
Let’s use a graphical depiction to get a different view of this rule. Figure 10.2 shows a matrix representing all possible combinations of results across two throws, and highlights the cells that involve a one on either the first or second throw. If you count up the cells in light blue you will see that there are 11 such cells. This shows why the addition rule gives a different answer from de Méré’s; if we were to simply add together the probabilities for the two throws as he did, then we would count (1,1) towards both, when it should really only be counted once.
10.2.4 Solving de Méré’s problem
Blaise Pascal used the rules of probability to come up with a solution to de Méré’s problem. First, he realized that computing the probability of at least one event out of a combination was tricky, whereas computing the probability that something does not occur across several events is relatively easy – it’s just the product of the probabilities of the individual events. Thus, rather than computing the probability of at least one six in four rolls, he instead computed the probability of no sixes across all rolls:
\(P(\text { no sixes in four rolls })=\frac{5}{6} * \frac{5}{6} * \frac{5}{6} * \frac{5}{6}=\left(\frac{5}{6}\right)^{4}=0.482\)
He then used the fact that the probability of no sixes in four rolls is the complement of at least one six in four rolls (thus they must sum to one), and used the rule of subtraction to compute the probability of interest:
\(P(\text { at least one six in four rolls })=1-\left(\frac{5}{6}\right)^{4}=0.517\)
de Méré’s gamble that he would throw at least one six in four rolls has a probability of greater than 0.5, explaning why de Méré made money on this bet on average.
But what about de Méré’s second bet? Pascal used the same trick:
\(P(\text { no double six in } 24 \text { rolls })=\left(\frac{35}{36}\right)^{24}=0.509\)
\(P(\text { at least one double } \operatorname{six} \text { in } 24 \text { rolls })=1-\left(\frac{35}{36}\right)^{24}=0.491\)
The probability of this outcome was slightly below 0.5, showing why de Méré lost money on average on this bet.


