8.3: Checking Model Assumptions using Graphs
- Page ID
- 319
Multiple regression methods using the model
\[\hat {y} = \beta _0 + \beta _1x_1 + \beta _2x_2 + \dots + \beta _kx_k\]
generally depend on the following four assumptions:
- the residuals of the model are nearly normal,
- the variability of the residuals is nearly constant,
- the residuals are independent, and
- each variable is linearly related to the outcome.
Simple and effective plots can be used to check each of these assumptions. We will consider the model for the auction data that uses the game condition and number of wheels as predictors.
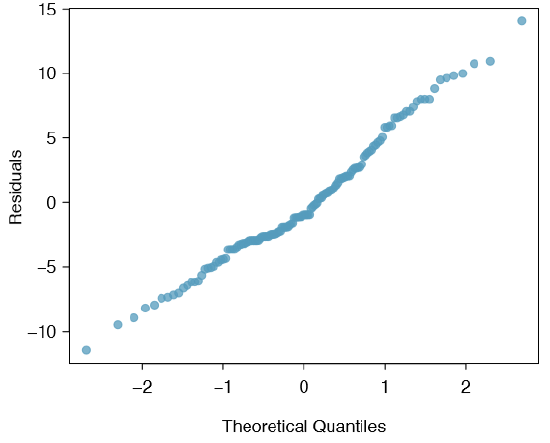
Normal probability plot. A normal probability plot of the residuals is shown in Figure \(\PageIndex{1}\). While the plot exhibits some minor irregularities, there are no outliers that might be cause for concern. In a normal probability plot for residuals, we tend to be most worried about residuals that appear to be outliers, since these indicate long tails in the distribution of residuals.
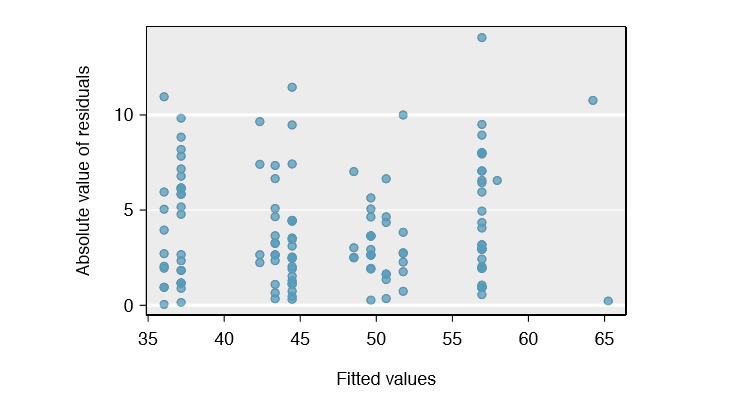
Absolute values of residuals against fitted values. A plot of the absolute value of the residuals against their corresponding fitted values (\(\hat {y}_i\)) is shown in Figure \(\PageIndex{2}\). This plot is helpful to check the condition that the variance of the residuals is approximately constant. We do not see any obvious deviations from constant variance in this example.
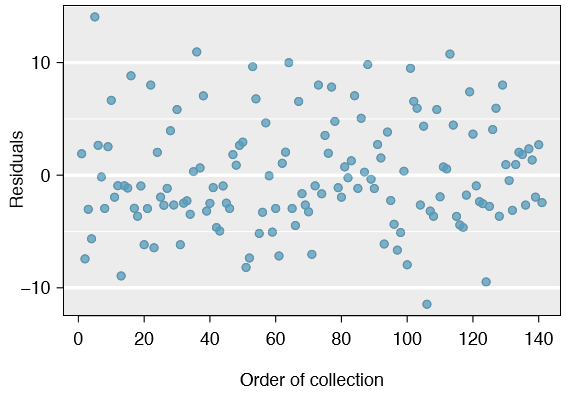
Residuals in order of their data collection. A plot of the residuals in the order their corresponding auctions were observed is shown in Figure \(\PageIndex{3}\). Such a plot is helpful in identifying any connection between cases that are close to one another, e.g. we could look for declining prices over time or if there was a time of the day when auctions tended to fetch a higher price. Here we see no structure that indicates a problem.12
Residuals against each predictor variable. We consider a plot of the residuals against the cond_new variable and the residuals against the wheels variable. These plots are shown in Figure \(\PageIndex{4}\). For the two-level condition variable, we are guaranteed not to see any remaining trend, and instead we are checking that the variability does not fluctuate across groups. In this example, when we consider the residuals against the wheels variable, we see some possible structure. There appears to be curvature in the residuals, indicating the relationship is probably not linear.
12An especially rigorous check would use time series methods. For instance, we could check whether consecutive residuals are correlated. Doing so with these residuals yields no statistically significant correlations.

It is necessary to summarize diagnostics for any model fit. If the diagnostics support the model assumptions, this would improve credibility in the ndings. If the diagnostic assessment shows remaining underlying structure in the residuals, we should try to adjust the model to account for that structure. If we are unable to do so, we may still report the model but must also note its shortcomings. In the case of the auction data, we report that there may be a nonlinear relationship between the total price and the number of wheels included for an auction. This information would be important to buyers and sellers; omitting this information could be a setback to the very people who the model might assist.
"All models are wrong, but some are useful" -George E.P. Box
The truth is that no model is perfect. However, even imperfect models can be useful. Reporting a awed model can be reasonable so long as we are clear and report the model's shortcomings.
Caution: do not report results when assumptions are grossly violated
While there is a little leeway in model assumptions, do not go too far. If model assumptions are very clearly violated, consider a new model, even if it means learning more statistical methods or hiring someone who can help.
TIP: Confidence intervals in multiple regression
Confidence intervals for coefficients in multiple regression can be computed using the same formula as in the single predictor model:
\[b_i \pm t^*_{df} SE_{b_i}\]
where \(t^*_{df}\) is the appropriate t value corresponding to the confidence level and model degrees of freedom, \(df = n - k - 1\).


