6.5: Small Sample Hypothesis Testing for a Proportion (Special Topic)
- Page ID
- 292
In this section we develop inferential methods for a single proportion that are appropriate when the sample size is too small to apply the normal model to \(\hat {p}\). Just like the methods related to the t distribution, these methods can also be applied to large samples.
When the Success-Failure Condition is Not Met
People providing an organ for donation sometimes seek the help of a special "medical consultant". These consultants assist the patient in all aspect of the surgery, with the goal of reducing the possibility of complications during the medical procedure and recovery. Patients might choose a consultant based in part on the historical complication rate of the consultant's clients. One consultant tried to attract patients by noting the average complication rate for liver donor surgeries in the US is about 10%, but her clients have only had 3 complications in the 62 liver donor surgeries she has facilitated. She claims this is strong evidence that her work meaningfully contributes to reducing complications (and therefore she should be hired!).
Exercise \(\PageIndex{1}\)
Exercise 6.42
We will let p represent the true complication rate for liver donors working with this consultant. Estimate p using the data, and label this value \(\hat {p}\).
Solution
The sample proportion: \(\hat {p} = \frac {3}{62} = 0.048\)
Example \(\PageIndex{1}\)
Is it possible to assess the consultant's claim using the data provided?
Solution
No. The claim is that there is a causal connection, but the data are observational. Patients who hire this medical consultant may have lower complication rates for other reasons.
While it is not possible to assess this causal claim, it is still possible to test for an association using these data. For this question we ask, could the low complication rate of \(\hat {p} = 0.048\) be due to chance?
Exercise \(\PageIndex{1}\)
Write out hypotheses in both plain and statistical language to test for the association between the consultant's work and the true complication rate, p, for this consultant's clients.
Solution
- H0: There is no association between the consultant's contributions and the clients' complication rate. In statistical language, p = 0.10.
- HA: Patients who work with the consultant tend to have a complication rate lower than 10%, i.e. p < 0.10.
Example \(\PageIndex{1}\)
In the examples based on large sample theory, we modeled \(\hat {p}\) using the normal distribution. Why is this not appropriate here?
Solution
The independence assumption may be reasonable if each of the surgeries is from a different surgical team. However, the success-failure condition is not satis ed. Under the null hypothesis, we would anticipate seeing \(62 \times 0.10 = 6.2\) complications, not the 10 required for the normal approximation.
The uncertainty associated with the sample proportion should not be modeled using the normal distribution. However, we would still like to assess the hypotheses from Exercise 6.44 in absence of the normal framework. To do so, we need to evaluate the possibility of a sample value (^p) this far below the null value, \(p_0 = 0.10\). This possibility is usually measured with a p-value.
The p-value is computed based on the null distribution, which is the distribution of the test statistic if the null hypothesis is true. Supposing the null hypothesis is true, we can compute the p-value by identifying the chance of observing a test statistic that favors the alternative hypothesis at least as strongly as the observed test statistic. This can be done using simulation.
Generating the null distribution and p-value by simulation
We want to identify the sampling distribution of the test statistic (\(\hat {p}\)) if the null hypothesis was true. In other words, we want to see how the sample proportion changes due to chance alone. Then we plan to use this information to decide whether there is enough evidence to reject the null hypothesis.
Under the null hypothesis, 10% of liver donors have complications during or after surgery. Suppose this rate was really no different for the consultant's clients. If this was the case, we could simulate 62 clients to get a sample proportion for the complication rate from the null distribution.
Each client can be simulated using a deck of cards. Take one red card, nine black cards, and mix them up. Then drawing a card is one way of simulating the chance a patient has a complication if the true complication rate is 10% for the data. If we do this 62 times and compute the proportion of patients with complications in the simulation, \(\hat {p}_{sim}\), then this sample proportion is exactly a sample from the null distribution.
An undergraduate student was paid $2 to complete this simulation. There were 5 simulated cases with a complication and 57 simulated cases without a complication, i.e. \(\hat {p}_{sim} = \frac {5}{62} = 0.081\).
Example \(\PageIndex{1}\)
Is this one simulation enough to determine whether or not we should reject the null hypothesis from Exercise 6.44? Explain.
Solution
No. To assess the hypotheses, we need to see a distribution of many \(\hat {p}_{sim}\), not just a single draw from this sampling distribution.
One simulation isn't enough to get a sense of the null distribution; many simulation studies are needed. Roughly 10,000 seems sufficient. However, paying someone to simulate 10,000 studies by hand is a waste of time and money. Instead, simulations are typically programmed into a computer, which is much more efficient.
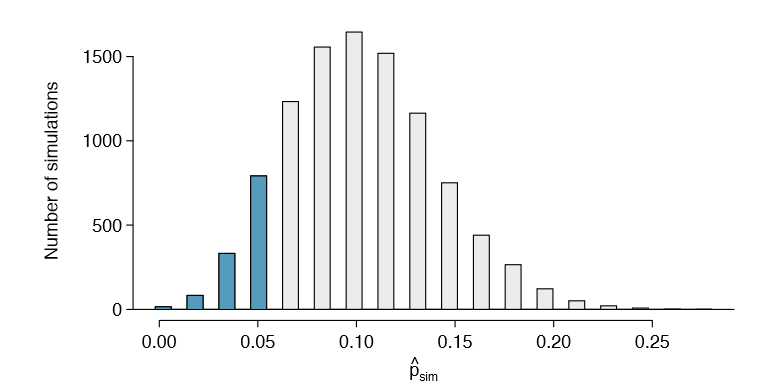
Figure 6.20 shows the results of 10,000 simulated studies. The proportions that are equal to or less than \(\hat {p} = 0.048\) are shaded. The shaded areas represent sample proportions under the null distribution that provide at least as much evidence as \(\hat {p}\) favoring the alternative hypothesis. There were 1222 simulated sample proportions with \(\hat {p}_{sim} \le 0.048\). We use these to construct the null distribution's left-tail area and nd the p-value:
\[ \text {left tail} = \frac {\text {Number of observed simulations with} \hat {p}_{sim} \le 0.048}{10000} \tag {6.47}\]
Of the 10,000 simulated \(\hat {p}_{sim}\), 1222 were equal to or smaller than \(\hat {p}\). Since the hypothesis test is one-sided, the estimated p-value is equal to this tail area: 0.1222.
Exercise \(\PageIndex{1}\)
Because the estimated p-value is 0.1222, which is larger than the signi cance level 0.05, we do not reject the null hypothesis. Explain what this means in plain language in the context of the problem.
Solution
There isn't sufficiently strong evidence to support an association between the consultant's work and fewer surgery complications.
Exercise \(\PageIndex{1}\)
Does the conclusion in Exercise 6.48 imply there is no real association between the surgical consultant's work and the risk of complications? Explain.
Solution
No. It might be that the consultant's work is associated with a reduction but that there isn't enough data to convincingly show this connection.
One-sided hypothesis test for p with a small sample
The p-value is always derived by analyzing the null distribution of the test statistic. The normal model poorly approximates the null distribution for \(\hat {p}\) when the success-failure condition is not satisfied. As a substitute, we can generate the null distribution using simulated sample proportions (\(\hat {p}_{sim}\)) and use this distribution to compute the tail area, i.e. the p-value.
We continue to use the same rule as before when computing the p-value for a twosided test: double the single tail area, which remains a reasonable approach even when the sampling distribution is asymmetric. However, this can result in p-values larger than 1 when the point estimate is very near the mean in the null distribution; in such cases, we write that the p-value is 1. Also, very large p-values computed in this way (e.g. 0.85), may also be slightly inated.
Exercise 6.48 said the p-value is estimated. It is not exact because the simulated null distribution itself is not exact, only a close approximation. However, we can generate an exact null distribution and p-value using the binomial model from Section 3.4.
Generating the exact null distribution and p-value
The number of successes in n independent cases can be described using the binomial model, which was introduced in Section 3.4. Recall that the probability of observing exactly k successes is given by
\[ P(\text {k successes}) = \binom {n}{k} p^k(1 - p)^{n-k} = \frac {n!}{k!(n - k)!} p^k (1 - p)^{n-k} \tag {6.50}\]
where p is the true probability of success. The expression \(\binom {n}{k}\) is read as n choose k, and the exclamation points represent factorials. For instance, 3! is equal to \(3 \times 2 \times 1 = 6, 4! \) is equal to \(4 \times 3 \times 2 \times 1 = 24\), and so on (see Section 3.4).
The tail area of the null distribution is computed by adding up the probability in Equation (6.50) for each k that provides at least as strong of evidence favoring the alternative hypothesis as the data. If the hypothesis test is one-sided, then the p-value is represented by a single tail area. If the test is two-sided, compute the single tail area and double it to get the p-value, just as we have done in the past.
Example \(\PageIndex{1}\)
Compute the exact p-value to check the consultant's claim that her clients' complication rate is below 10%.
Solution
Exactly k = 3 complications were observed in the n = 62 cases cited by the consultant. Since we are testing against the 10% national average, our null hypothesis is p = 0.10. We can compute the p-value by adding up the cases where there are 3 or fewer complications:
\[ \text {p-value} = \sum \limits ^3_{j=0} \binom {n}{j} p^j(1 - p)^{n-j}\]
\[ = \sum \limits ^3_{j=0} \binom {62}{j} 0.1^j(1 - 0.1)^{62-j}\]
\[ = \binom {62}{0} 0.1^0(1 - 0.1)^{62-0} + \binom {62}{1} 0.1^1(1 - 0.1)^{62-1} + \binom {62}{2}0.1^2(1 - 0.1)^{62-2} + \binom {62}{3} 0.1^3(1 - 0.1)^{62-3}\]
\[= 0.0015 + 0.0100 + 0.0340 + 0.0755\]
\[= 0.1210\]
This exact p-value is very close to the p-value based on the simulations (0.1222), and we come to the same conclusion. We do not reject the null hypothesis, and there is not statistically signi cant evidence to support the association.
If it were plotted, the exact null distribution would look almost identical to the simulated null distribution shown in Figure 6.20 on page 290.
Using simulation for goodness of fit tests
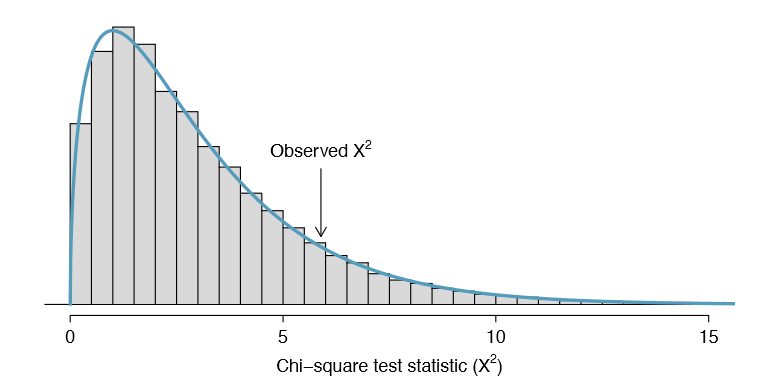
Simulation methods may also be used to test goodness of t. In short, we simulate a new sample based on the purported bin probabilities, then compute a chi-square test statistic \(X^2_{sim}\). We do this many times (e.g. 10,000 times), and then examine the distribution of these simulated chi-square test statistics. This distribution will be a very precise null distribution for the test statistic X2 if the probabilities are accurate, and we can nd the upper tail of this null distribution, using a cutoff of the observed test statistic, to calculate the p-value.
Example \(\PageIndex{1}\)
Section 6.3 introduced an example where we considered whether jurors were racially representative of the population. Would our ndings differ if we used a simulation technique?
Solution
Since the minimum bin count condition was satis ed, the chi-square distribution is an excellent approximation of the null distribution, meaning the results should be very similar. Figure 6.21 shows the simulated null distribution using 100,000 simulated \(X^2_{sim}\) values with an overlaid curve of the chi-square distribution. The distributions are almost identical, and the p-values are essentially indistinguishable: 0.115 for the simulated null distribution and 0.117 for the theoretical null distribution.