4.6: Inference for other Estimators
- Page ID
- 284
The sample mean is not the only point estimate for which the sampling distribution is nearly normal. For example, the sampling distribution of sample proportions closely resembles the normal distribution when the sample size is sufficiently large. In this section, we introduce a number of examples where the normal approximation is reasonable for the point estimate. Chapters 5 and 6 will revisit each of the point estimates you see in this section along with some other new statistics.
We make another important assumption about each point estimate encountered in this section: the estimate is unbiased. A point estimate is unbiased if the sampling distribution of the estimate is centered at the parameter it estimates. That is, an unbiased estimate does not naturally over or underestimate the parameter. Rather, it tends to provide a "good" estimate. The sample mean is an example of an unbiased point estimate, as are each of the examples we introduce in this section.
Finally, we will discuss the general case where a point estimate may follow some distribution other than the normal distribution. We also provide guidance about how to handle scenarios where the statistical techniques you are familiar with are insufficient for the problem at hand.
Confidence intervals for nearly normal point estimates
In Section 4.2, we used the point estimate \(\bar {x}\) with a standard error \(SE_{\bar {x}}\) to create a 95% confidence interval for the population mean:
\[\bar {x} \pm 1.96 \times SE_{\bar {x}} \label {4.44}\]
We constructed this interval by noting that the sample mean is within 1.96 standard errors of the actual mean about 95% of the time. This same logic generalizes to any unbiased point estimate that is nearly normal. We may also generalize the confidence level by using a place-holder z^*.
General confidence interval for the normal sampling distribution case
A confidence interval based on an unbiased and nearly normal point estimate is
\[\text {point estimate} \pm z^* SE \label{4.45}\]
where z^* is selected to correspond to the confidence level, and SE represents the standard error. The value z^*SE is called the margin of error.
Generally the standard error for a point estimate is estimated from the data and computed using a formula. For example, the standard error for the sample mean is
\[SE_{\bar {x}} = \dfrac {s}{\sqrt {n}}\]
In this section, we provide the computed standard error for each example and exercise without detailing where the values came from. In future chapters, you will learn to fill in these and other details for each situation.
Example \(\PageIndex{1}\)
In Exercise 4.1, we computed a point estimate for the average difference in run times between men and women: \(\bar {x}_{women} - \bar {x}_{men} = 14.48\) minutes. This point estimate is associated with a nearly normal distribution with standard error SE = 2.78 minutes. What is a reasonable 95% confidence interval for the difference in average run times?
Solution
The normal approximation is said to be valid, so we apply Equation \ref{4.45}:
\[ \text {point estimate} \pm z^*SE \rightarrow 14.48 \pm 1.96 \times 2.78 \rightarrow (9.03, 19.93)\]
Thus, we are 95% confident that the men were, on average, between 9.03 and 19.93 minutes faster than women in the 2012 Cherry Blossom Run. That is, the actual average difference is plausibly between 9.03 and 19.93 minutes with 95% confidence.
Example \(\PageIndex{2}\)
Does Example \(\PageIndex{1}\) guarantee that if a husband and wife both ran in the race, the husband would run between 9.03 and 19.93 minutes faster than the wife?
Solution
Our confidence interval says absolutely nothing about individual observations. It only makes a statement about a plausible range of values for the average difference between all men and women who participated in the run.
Exercise \(\PageIndex{1}\)
What \(z^*\) would be appropriate for a 99% confidence level? For help, see Figure 4.10 on page 169.
Solution
We seek \(z^*\) such that 99% of the area under the normal curve will be between the Z scores \(-z^*\) and \(z^*\). Because the remaining 1% is found in the tails, each tail has area 0.5%, and we can identify \(-z^*\) by looking up 0.0050 in the normal probability table: z^* = 2.58. See also Figure 4.10 on page 169.
\[\hat {p} \pm z^*SE_{\hat {p}} \rightarrow 0.45 \pm 1.65 \times 0.05 \rightarrow (0.3675, 0.5325)\]
Thus, we are 90% confident that between 37% and 53% of the participants were men.
Exercise \(\PageIndex{2}\)
The proportion of men in the run10Samp sample is \(\hat {p} = 0.45\). This sample meets certain conditions that ensure \(\hat {p}\) will be nearly normal, and the standard error of the estimate is \(SE_{\hat {p}} = 0.05\). Create a 90% confidence interval for the proportion of participants in the 2012 Cherry Blossom Run who are men.
Answer
We use \(z^* = 1.65\) (see Exercise 4.17 on page 170), and apply the general confidence interval formula:
Hypothesis Testing for Nearly Normal Point Estimates
Just as the confidence interval method works with many other point estimates, we can generalize our hypothesis testing methods to new point estimates. Here we only consider the p-value approach, introduced in Section 4.3.4, since it is the most commonly used technique and also extends to non-normal cases.
Hypothesis testing using the normal model
- First write the hypotheses in plain language, then set them up in mathematical notation.
- Identify an appropriate point estimate of the parameter of interest.
- Verify conditions to ensure the standard error estimate is reasonable and the point estimate is nearly normal and unbiased.
- Compute the standard error. Draw a picture depicting the distribution of the estimate under the idea that \(H_0\) is true. Shade areas representing the p-value.
- Using the picture and normal model, compute the test statistic (Z score) and identify the p-value to evaluate the hypotheses. Write a conclusion in plain language.
Exercise \(\PageIndex{3}\): sulphinpyrazone
A drug called sulphinpyrazone was under consideration for use in reducing the death rate in heart attack patients. To determine whether the drug was effective, a set of 1,475 patients were recruited into an experiment and randomly split into two groups: a control group that received a placebo and a treatment group that received the new drug. What would be an appropriate null hypothesis? And the alternative?
Answer
The skeptic's perspective is that the drug does not work at reducing deaths in heart attack patients (H0), while the alternative is that the drug does work (HA).
We can formalize the hypotheses from Exercise \(\PageIndex{3}\) by letting pcontrol and ptreatment represent the proportion of patients who died in the control and treatment groups, respectively. Then the hypotheses can be written as
- H0 : \(p_{control} = p_{treatment}\) (the drug doesn't work)
- HA : \(p_{control} > p_{treatment}\) (the drug works)
or equivalently,
- H0 : \(p_{control} - p_{treatment}\) = 0 (the drug doesn't work)
- HA : \(p_{control} - p_{treatment}\) > 0 (the drug works)
Strong evidence against the null hypothesis and in favor of the alternative would correspond to an observed difference in death rates,
\[point estimate = \hat {p}_{control} - \hat {p}_{treatment}\]
being larger than we would expect from chance alone. This difference in sample proportions represents a point estimate that is useful in evaluating the hypotheses.
Example \(\PageIndex{3}\)
We want to evaluate the hypothesis setup from Exericse 4.50 using data from the actual study (Anturane Reinfarction Trial Research Group. 1980. Sulfinpyrazone in the prevention of sudden death after myocardial infarction. New England Journal of Medicine 302(5):250-256). In the control group, 60 of 742 patients died. In the treatment group, 41 of 733 patients died. The sample difference in death rates can be summarized as
\[point estimate = \hat {p}_{control} - \hat {p}_{treatment} = \dfrac {60}{742} - \dfrac {41}{733} = 0.025\]
This point estimate is nearly normal and is an unbiased estimate of the actual difference in death rates. The standard error of this sample difference is SE = 0.013. Evaluate the hypothesis test at a 5% significance level: \(\alpha = 0.05\).
Solution
We would like to identify the p-value to evaluate the hypotheses. If the null hypothesis is true, then the point estimate would have come from a nearly normal distribution, like the one shown in Figure \(\PageIndex{1}\).
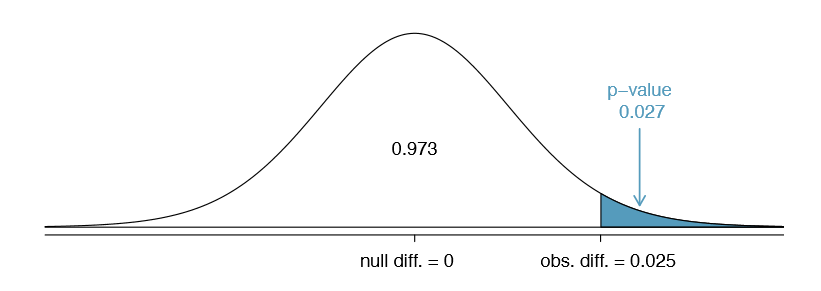
The distribution is centered at zero since \(p_{control} - p_{treatment} = 0\) under the null hypothesis. Because a large positive difference provides evidence against the null hypothesis and in favor of the alternative, the upper tail has been shaded to represent the p-value. We need not shade the lower tail since this is a one-sided test: an observation in the lower tail does not support the alternative hypothesis.
The p-value can be computed by using the Z score of the point estimate and the normal probability table.
\[Z = \dfrac {point estimate - null value}{SE_{point estimate}} = \dfrac {0.025 - 0}{0.013} = 1.92 \label{4.52}\]
Examining Z in the normal probability table, we nd that the lower unshaded tail is about 0.973. Thus, the upper shaded tail representing the p-value is
\[p-value = 1 - 0.973 = 0.027\]
Because the p-value is less than the significance level (\(\alpha = 0.05)\), we say the null hypothesis is implausible. That is, we reject the null hypothesis in favor of the alternative and conclude that the drug is effective at reducing deaths in heart attack patients.
The Z score in Equation \ref{4.52} is called a test statistic. In most hypothesis tests, a test statistic is a particular data summary that is especially useful for computing the p-value and evaluating the hypothesis test. In the case of point estimates that are nearly normal, the test statistic is the Z score.
Test statistic
A test statistic is a special summary statistic that is particularly useful for evaluating a hypothesis test or identifying the p-value. When a point estimate is nearly normal, we use the Z score of the point estimate as the test statistic. In later chapters we encounter situations where other test statistics are helpful.
Non-Normal Point Estimates
We may apply the ideas of confidence intervals and hypothesis testing to cases where the point estimate or test statistic is not necessarily normal. There are many reasons why such a situation may arise:
- the sample size is too small for the normal approximation to be valid;
- the standard error estimate may be poor; or
- the point estimate tends towards some distribution that is not the normal distribution.
For each case where the normal approximation is not valid, our rst task is always to understand and characterize the sampling distribution of the point estimate or test statistic. Next, we can apply the general frameworks for confidence intervals and hypothesis testing to these alternative distributions.
When to Retreat
Statistical tools rely on conditions. When the conditions are not met, these tools are unreliable and drawing conclusions from them is treacherous. The conditions for these tools typically come in two forms.
- The individual observations must be independent. A random sample from less than 10% of the population ensures the observations are independent. In experiments, we generally require that subjects are randomized into groups. If independence fails, then advanced techniques must be used, and in some such cases, inference may not be possible.
- Other conditions focus on sample size and skew. For example, if the sample size is too small, the skew too strong, or extreme outliers are present, then the normal model for the sample mean will fail.
Verification of conditions for statistical tools is always necessary. Whenever conditions are not satisfied for a statistical technique, there are three options. The rst is to learn new methods that are appropriate for the data. The second route is to consult a statistician. The third route is to ignore the failure of conditions. This last option effectively invalidates any analysis and may discredit novel and interesting findings.
If you work at a university, then there may be campus consulting services to assist you. Alternatively, there are many private consulting firms that are also available for hire.
Finally, we caution that there may be no inference tools helpful when considering data that include unknown biases, such as convenience samples. For this reason, there are books, courses, and researchers devoted to the techniques of sampling and experimental design. See Sections 1.3-1.5 for basic principles of data collection.


