3.3: Cautions
- Page ID
- 7800
Sensitivity to Outliers
The correlation coefficient and the (coefficients of the) LSRL are built out of means and standard deviations and therefore the following fact is completely unsurprising
FACT 3.3.1. The correlation coefficient and the (coefficients of the) LSRL are very sensitive to outliers.
What perhaps is surprising here is that the outliers for bivariate data are a little different from those for 1-variable data.
DEFINITION 3.3.2. An outlier for a bivariate quantitative dataset is one which is far away from the curve which has been identified as underlying the shape of the scatterplot of that data. In particular, a point \((x,y)\) can be a bivariate outlier even if both \(x\) is not an outlier for the independent variable data considered alone and \(y\) is not an outlier for the dependent variable data alone.
EXAMPLE 3.3.3. Suppose we add one more point (90,30) to the dataset in Exam- ple 3.1.4. Neither the \(x\)- nor \(y\)-coordinates of this point are outliers with respect to their respective single-coordinate datasets, but it is nevertheless clearly a bivariate outlier, as can be seen in the new scatterplot
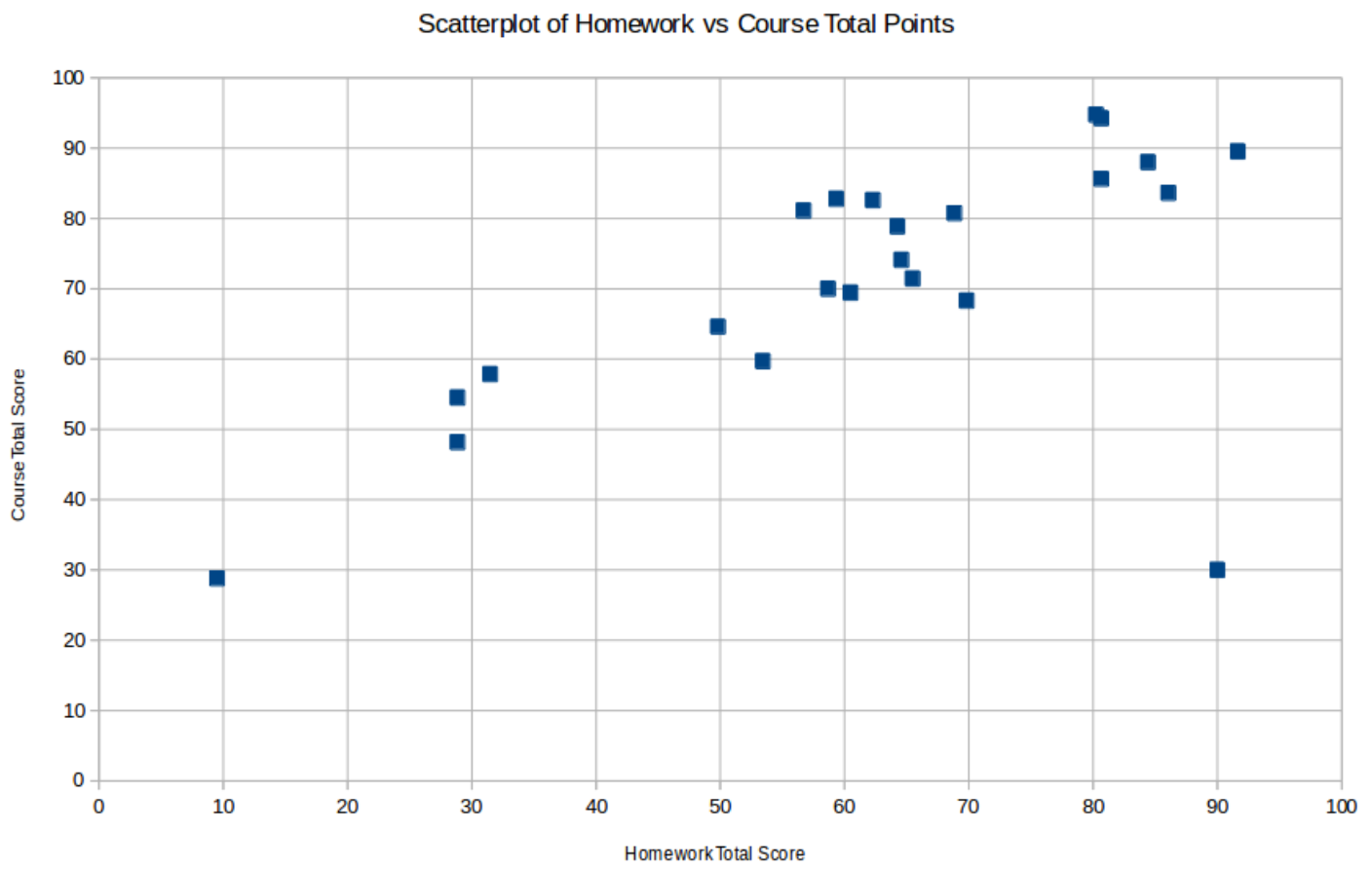
In fact recomputing the correlation coefficient and LSRL, we find quite a change from what we found before, in Example 3.1.4: \[r=.704\qquad\text{[which used to be } .935]\] and \[\widehat{y}=.529x+38.458\qquad\text{[which used to be }.754x+26.976]\] all because of one additional point!
Causation
The attentive reader will have noticed that we started our discussion of bivariate data by saying we hoped to study when one thing causes another. However, what we’ve actually done instead is find correlation between variables, which is quite a different thing.
Now philosophers have discussed what exactly causation is for millennia, so certainly it is a subtle issue that we will not resolve here. In fact, careful statisticians usually dodge the complexities by talking about relationships, association, and, of course, the correlation coefficient, being careful always not to commit to causation – at least based only on an analysis of the statistical data.
As just one example, where we spoke about the meaning of the square \(r^2\) of the correlation coefficient (we called it Fact 2.3.3), we were careful to say that \(r^2\) measures the variation of the dependent variable which is associated with the variation of the independent variable. A more reckless description would have been to say that one caused the other – but don’t fall into that trap!
This would be a bad idea because (among other reasons) the correlation coefficient is symmetric in the choice of explanatory and response variables (meaning \(r\) is the same no matter which is chosen for which role), while any reasonable notion of causation is asymmetric. E.g., while the correlation is exactly the same very large value with either variable being \(x\) and which \(y\), most people would say that smoking causes cancer and not the other way6!
We do need to make one caution about this caution, however. If there is a causal relationship between two variables that are being studied carefully, then there will be correlation. So, to quote the great data scientist Edward Tufte ,
Correlation is not causation but it sure is a hint.
The first part of this quote (up to the “but”) is much more famous and, as a very first step, is a good slogan to live by. Those with a bit more statistical sophistication might instead learn this version, though. A more sophisticated-sounding version, again due to Tufte , is
Empirically observed covariation is a necessary but not sufficient condition for causality.
Extrapolation
We have said that visual intuition often allows humans to sketch fairly good approximations of the LSRL on a scatterplot, so long as the correlation coefficient tells us there is a strong linear association. If the diligent reader did that with the first scatterplot in Example 3.1.4, probably the resulting line looked much like the line which LibreOffice Calc produced – except humans usually sketch their line all the way to the left and right edges of the graphics box. Automatic tools like LibreOffice Calc do not do that, for a reason.
[def:extrapolation] Given a bivariate quantitative dataset and associated LSRL with equation \(\widehat{y}=mx+b\), the process of guessing that the value of the dependent variable in this relationship to have the value \(mx_0+b\), for \(x_0\) any value for the independent variable which does not satisfy \(x_{min}\le x_0\le x_{max}\) [so, instead, either \(x_0<x_{min}\) or \(x_0>x_{max}\)], is called extrapolation.
Extrapolation is considered a bad, or at least risky, practice. The idea is that we used the evidence in the dataset \(\{(x_1,y_1), \dots , (x_n,y_n)\}\) to build the LSRL, but, by definition, all of this data lies in the interval on the \(x\)-axis from \(x_{min}\) to \(x_{max}\). There is literally no evidence from this dataset about what the relationship between our chosen explanatory and response variables will be for \(x\) outside of this interval. So in the absence of strong reasons to believe that the precise linear relationship described by the LSRL will continue for more \(x\)’s, we should not assume that it does, and therefore we should not use the LSRL equation to guess values by extrapolation.
The fact is, however, that often the best thing we can do with available information when we want to make predictions out into uncharted territory on the \(x\)-axis is extrapolation. So while it is perilous, it is reasonable to extrapolate, so long as you are clear about what exactly you are doing.
EXAMPLE 3.3.5. Using again the statistics students’ homework and total course points data from Example 3.1.4, suppose the course instructor wanted to predict what would be the total course points for a student who had earned a perfect \(100\) points on their homework. Plugging into the LSRL, this would have yielded a guess of \(.754\cdot100+26.976=102.376\). Of course, this would have been impossible, since the maximum possible total course score was \(100\). Moreover, making this guess is an example of extrapolation, since the \(x\) value of \(100\) is beyond the largest \(x\) value of \(x_{max}=92\) in the dataset. Therefore we should not rely on this guess – as makes sense, since it is invalid by virtue of being larger than \(100\).
Simpson’s Paradox
Our last caution is not so much a way using the LSRL can go wrong, but instead a warning to be ready for something very counter-intuitive to happen – so counter-intuitive, in fact, that it is called a paradox.
It usually seems reasonable that if some object is cut into two pieces, both of which have a certain property, then probably the whole object also has that same property. But if the object in question is a population and the property is has positive correlation, then maybe the unreasonable thing happens.
DEFINITION 3.3.6. Suppose we have a population for which we have a bivariate quantitative dataset. Suppose further that the population is broken into two (or more) subpopulations for all of which the correlation between the two variables is positive, but the correlation of the variables for the whole dataset is negative. Then this situation is called Simpson’s Paradox. [It’s also called Simpson’s Paradox if the role of positive and negative is reversed in our assumptions.]
The bad news is that Simpson’s paradox can happen.
EXAMPLE 3.3.7 Let \(\ P=\{(0,1), (1,0), (9,10), (10,9)\}\) be a bivariate dataset, which is broken into the two subpopulations \(\ P_1=\{(0,1), (1,0)\}\) and \(\ P_2=\{(9,10), (10,9)\}\). Then the correlation coefficients of both \(\ P_1\) and \(\ P_2\) are \(r=-1\), but the correlation of all of \(\ P\) is \(r=.9756\). This is Simpson’s Paradox!
Or, in applications, we can have situations like
EXAMPLE 3.3.8. Suppose we collect data on two sections of a statistics course, in particular on how many hours per work the individual students study for the course and how they do in the course, measured by their total course points at the end of the semester. It is possible that there is a strong positive correlation between these variables for each section by itself, but there is a strong negative correlation when we put all the students into one dataset. In other words, it is possible that the rational advice, based on both individual sections, is study more and you will do better in the course, but that the rational advice based on all the student data put together is study less and you will do better.


