9.2: Comparison of Two Population Means - Small, Independent Samples
- Page ID
- 573
- To learn how to construct a confidence interval for the difference in the means of two distinct populations using small, independent samples.
- To learn how to perform a test of hypotheses concerning the difference between the means of two distinct populations using small, independent samples.
When one or the other of the sample sizes is small, as is often the case in practice, the Central Limit Theorem does not apply. We must then impose conditions on the population to give statistical validity to the test procedure. We will assume that both populations from which the samples are taken have a normal probability distribution and that their standard deviations are equal.
Confidence Intervals
When the two populations are normally distributed and have equal standard deviations, the following formula for a confidence interval for \(\mu _1-\mu _2\) is valid.
\[(\bar{x_1}-\bar{x_2})\pm t_{\alpha /2}\sqrt{s_{p}^{2}\left ( \dfrac{1}{n_1}+\dfrac{1}{n_2} \right )} \label{eq1} \]
where
\[s_{p}^{2}=\dfrac{(n_1-1)s_{1}^{2}+(n_2-1)s_{2}^{2}}{n_1+n_2-2} \nonumber \]
The number of degrees of freedom is
\[df=n_1+n_2-2. \nonumber \]
The samples must be independent, the populations must be normal, and the population standard deviations must be equal. “Small” samples means that either \(n_1<30\) or \(n_2<30\).
The quantity \(s_{p}^{2}\) is called the pooled sample variance. It is a weighted average of the two estimates \(s_{1}^{2}\) and \(s_{2}^{2}\) of the common variance \(\sigma _{1}^{2}=\sigma _{2}^{2}\) of the two populations.
A software company markets a new computer game with two experimental packaging designs. Design \(1\) is sent to \(11\) stores; their average sales the first month is \(52\) units with sample standard deviation \(12\) units. Design \(2\) is sent to \(6\) stores; their average sales the first month is \(46\) units with sample standard deviation \(10\) units. Construct a point estimate and a \(95\%\) confidence interval for the difference in average monthly sales between the two package designs.
Solution
The point estimate of \(\mu _1-\mu _2\) is
\[\bar{x_1}-\bar{x_2}=52-46-6 \nonumber \]
In words, we estimate that the average monthly sales for Design \(1\) is \(6\) units more per month than the average monthly sales for Design \(2\).
To apply the formula for the confidence interval (Equation \ref{eq1}), we must find \(t_{\alpha /2}\). The \(95\%\) confidence level means that \(\alpha =1-0.95=0.05\) so that \(t_{\alpha /2}=t_{0.025}\). From Figure 7.1.6, in the row with the heading \(df=11+6-2=15\) we read that \(t_{0.025}=2.131\). From the formula for the pooled sample variance we compute
\[s_{p}^{2}=\dfrac{(n_1-1)s_{1}^{2}+(n_2-1)s_{2}^{2}}{n_1+n_2-2}=\dfrac{(10)(12)^2+(5)(10)^2}{15}=129.\bar{3} \nonumber \]
Thus
\[(\bar{x_1}-\bar{x_2})\pm t_\alpha /2\sqrt{s_{p}^{2}\left ( \dfrac{1}{n_1}+\dfrac{1}{n_2} \right )}=6\pm (2.131)\sqrt{129.\bar{3}\left ( \dfrac{1}{11}+\dfrac{1}{6} \right )}\approx 6\pm 12.3 \nonumber \]
We are \(95\%\) confident that the difference in the population means lies in the interval \([-6.3,18.3]\), in the sense that in repeated sampling \(95\%\) of all intervals constructed from the sample data in this manner will contain \(\mu _1-\mu _2\). Because the interval contains both positive and negative values the statement in the context of the problem is that we are \(95\%\) confident that the average monthly sales for Design \(1\) is between \(18.3\) units higher and \(6.3\) units lower than the average monthly sales for Design \(2\).
Hypothesis Testing
Testing hypotheses concerning the difference of two population means using small samples is done precisely as it is done for large samples, using the following standardized test statistic. The same conditions on the populations that were required for constructing a confidence interval for the difference of the means must also be met when hypotheses are tested.
\[T=\dfrac{(\bar{x_1}-\bar{x_2})-D_0}{\sqrt{s_{p}^{2}\left ( \dfrac{1}{n_1}+\dfrac{1}{n_2}\right )}} \nonumber \]
where
\[ s_{p}^{2}=\dfrac{(n_1-1)s_{1}^{2}+(n_2-1)s_{2}^{2}}{n_1+n_2-2} \nonumber \]
The test statistic has Student’s t-distribution with \(df=n_1+n_2-2\) degrees of freedom.
The samples must be independent, the populations must be normal, and the population standard deviations must be equal. “Small” samples means that either \(n_1<30\) or \(n_2<30\).
Refer to Example \(\PageIndex{1}\) concerning the mean sales per month for the same computer game but sold with two package designs. Test at the \(1\%\) level of significance whether the data provide sufficient evidence to conclude that the mean sales per month of the two designs are different. Use the critical value approach.
Solution
- Step 1. The relevant test is
\[H_0: \mu _1-\mu _2=0 \nonumber \]
vs.
\[H_a: \mu _1-\mu _2\neq 0\; \; @\; \; \alpha =0.01 \nonumber \]
- Step 2. Since the samples are independent and at least one is less than \(30\) the test statistic is
\[T=\dfrac{(\bar{x_1}-\bar{x_2})-D_0}{\sqrt{s_{p}^{2}\left ( \dfrac{1}{n_1}+\dfrac{1}{n_2}\right )}} \nonumber \]
which has Student’s \(t\)-distribution with \(df=11+6-2=15\) degrees of freedom.
- Step 3. Inserting the data and the value \(D_0=0\) into the formula for the test statistic gives
\[\begin{align*} T&=\dfrac{(\bar{x_1}-\bar{x_2})-D_0}{\sqrt{s_{p}^{2}\left ( \dfrac{1}{n_1}+\dfrac{1}{n_2}\right )}} \\[4pt] &=\dfrac{(52-46)-0}{\sqrt{129.\bar{3}\left ( \dfrac{1}{11}+\dfrac{1}{6} \right )}} \\[4pt] &=1.040 \end{align*} \nonumber \]
- Step 4. Since the symbol in \(H_a\) is “\(\neq\)” this is a two-tailed test, so there are two critical values, \(\pm t_{\alpha /2}=\pm t_{0.005}\). From the row in Figure 7.1.6 with the heading \(df=15\) we read off \(t_{0.005}=2.947\). The rejection region is \((-\infty ,-2.947]\cup [2.947,\infty )\).
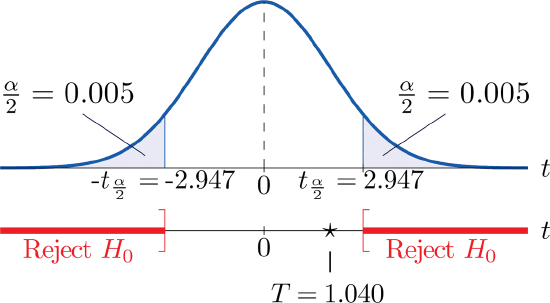
- Step 5. As shown in Figure \(\PageIndex{1}\) the test statistic does not fall in the rejection region. The decision is not to reject \(H_0\). In the context of the problem our conclusion is:
The data do not provide sufficient evidence, at the \(1\%\) level of significance, to conclude that the mean sales per month of the two designs are different.
Perform the test of Example \(\PageIndex{2}\) using the \(p\)-value approach.
Solution
The first three steps are identical to those in Example \(\PageIndex{2}\).
- Step 4. Because the test is two-tailed the observed significance or \(p\)-value of the test is the double of the area of the right tail of Student’st-distribution, with \(15\) degrees of freedom, that is cut off by the test statistic \(T=1.040\). We can only approximate this number. Looking in the row of Figure 7.1.6 headed \(df=15\), the number \(1.040\) is between the numbers \(0.866\) and \(1.341\), corresponding to \(t_{0.200}\) and \(t_{0.100}\). The area cut off by \(t=0.866\) is \(0.200\) and the area cut off by \(t=1.341\) is \(0.100\). Since \(1.040\) is between \(0.866\) and \(1.341\) the area it cuts off is between \(0.200\) and \(0.100\). Thus the \(p\)-value (since the area must be doubled) is between \(0.400\) and \(0.200\).
- Step 5. Since \(p>0.200>0.01,\; \; p>\alpha\), so the decision is not to reject the null hypothesis:
The data do not provide sufficient evidence, at the \(1\%\) level of significance, to conclude that the mean sales per month of the two designs are different.
Key Takeaway
- In the context of estimating or testing hypotheses concerning two population means, “small” samples means that at least one sample is small. In particular, even if one sample is of size \(30\) or more, if the other is of size less than \(30\) the formulas of this section must be used.
- A confidence interval for the difference in two population means is computed using a formula in the same fashion as was done for a single population mean.


