6.3: The Sample Proportion
- Page ID
- 571
- To recognize that the sample proportion \(\hat{p}\) is a random variable.
- To understand the meaning of the formulas for the mean and standard deviation of the sample proportion.
- To learn what the sampling distribution of \(\hat{p}\) is when the sample size is large.
Often sampling is done in order to estimate the proportion of a population that has a specific characteristic, such as the proportion of all items coming off an assembly line that are defective or the proportion of all people entering a retail store who make a purchase before leaving. The population proportion is denoted \(p\) and the sample proportion is denoted \(\hat{p}\). Thus if in reality \(43\%\) of people entering a store make a purchase before leaving,
\[p = 0.43 \nonumber \]
if in a sample of \(200\) people entering the store, \(78\) make a purchase,
\[\hat{p}=\dfrac{78}{200}=0.39. \nonumber \]
The sample proportion is a random variable: it varies from sample to sample in a way that cannot be predicted with certainty. Viewed as a random variable it will be written \(\hat{P}\). It has a mean \(μ_{\hat{P}}\) and a standard deviation \(σ_{\hat{P}}\). Here are formulas for their values.
Suppose random samples of size \(n\) are drawn from a population in which the proportion with a characteristic of interest is \(p\). The mean \(μ_{\hat{P}}\) and standard deviation \(σ_{\hat{P}}\) of the sample proportion \(\hat{P}\) satisfy
\[μ_{\hat{P}}=p \nonumber \]
and
\[σ_{\hat{P}}= \sqrt{\dfrac{pq}{n}} \nonumber \]
where \(q=1−p\).
The Central Limit Theorem has an analogue for the population proportion \(\hat{p}\). To see how, imagine that every element of the population that has the characteristic of interest is labeled with a \(1\), and that every element that does not is labeled with a \(0\). This gives a numerical population consisting entirely of zeros and ones. Clearly the proportion of the population with the special characteristic is the proportion of the numerical population that are ones; in symbols,
\[p=\dfrac{\text{number of 1s}}{N} \nonumber \]
But of course the sum of all the zeros and ones is simply the number of ones, so the mean \(μ\) of the numerical population is
\[μ=\dfrac{ \sum x}{N}= \dfrac{\text{number of 1s}}{N} \nonumber \]
Thus the population proportion \(p\) is the same as the mean \(μ\) of the corresponding population of zeros and ones. In the same way the sample proportion \(\hat{p}\) is the same as the sample mean \(\bar{x}\). Thus the Central Limit Theorem applies to \(\hat{p}\). However, the condition that the sample be large is a little more complicated than just being of size at least \(30\).
The Sampling Distribution of the Sample Proportion
For large samples, the sample proportion is approximately normally distributed, with mean \(μ_{\hat{P}}=p\) and standard deviation \(\sigma _{\hat{P}}=\sqrt{\frac{pq}{n}}\).
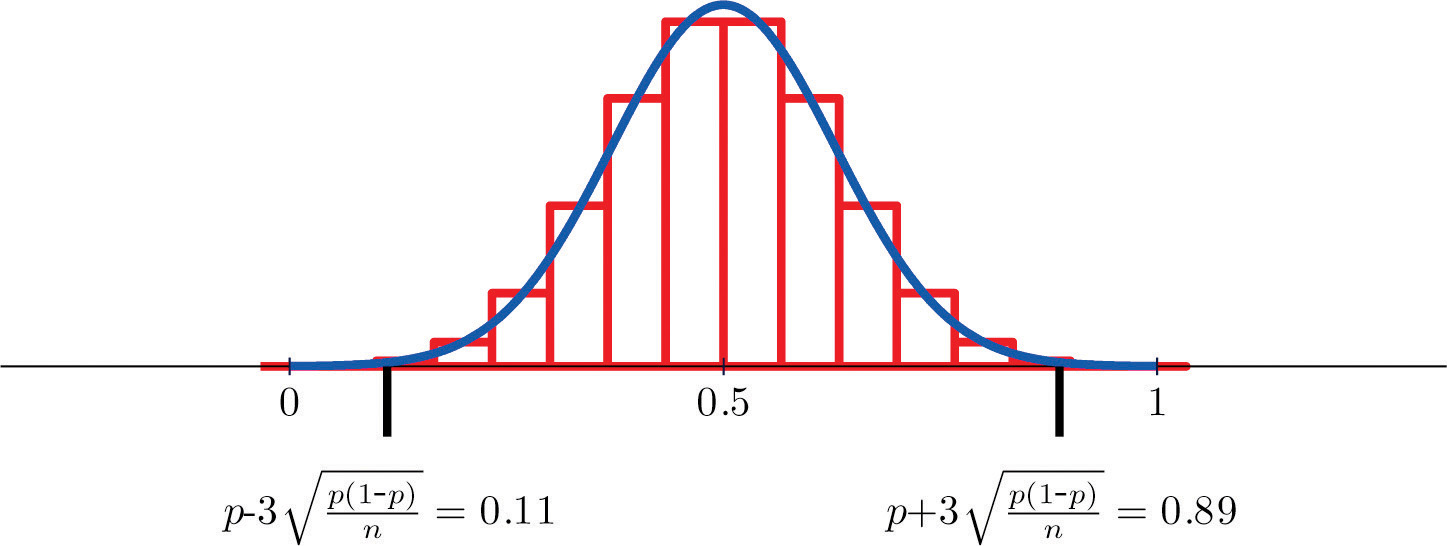
A sample is large if the interval \(\left [ p-3\sigma _{\hat{p}},\, p+3\sigma _{\hat{p}} \right ]\) lies wholly within the interval \([0,1]\).
In actual practice \(p\) is not known, hence neither is \(σ_{\hat{P}}\). In that case in order to check that the sample is sufficiently large we substitute the known quantity \(\hat{p}\) for \(p\). This means checking that the interval
\[\left [ \hat{p}-3\sqrt{\frac{\hat{p}(1-\hat{p})}{n}},\, \hat{p}+3\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \right ] \nonumber \]
lies wholly within the interval \([0,1]\). This is illustrated in the examples.
Figure \(\PageIndex{1}\) shows that when \(p = 0.1\), a sample of size \(15\) is too small but a sample of size \(100\) is acceptable.
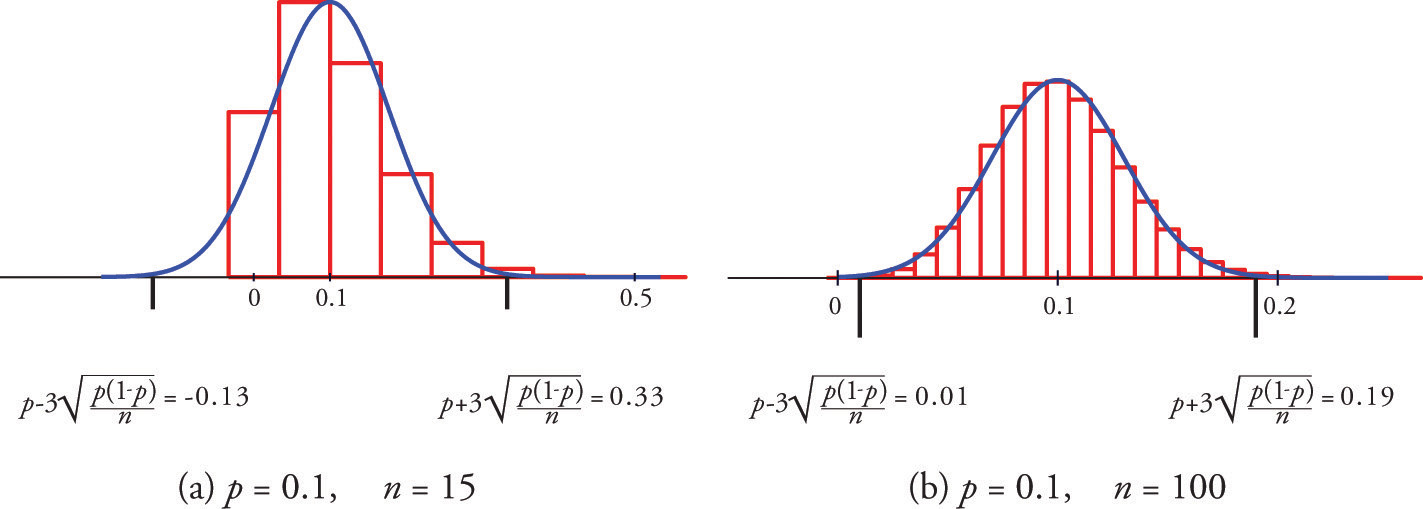
Figure \(\PageIndex{2}\) shows that when \(p=0.5\) a sample of size \(15\) is acceptable.
Suppose that in a population of voters in a certain region \(38\%\) are in favor of particular bond issue. Nine hundred randomly selected voters are asked if they favor the bond issue.
- Verify that the sample proportion \(\hat{p}\) computed from samples of size \(900\) meets the condition that its sampling distribution be approximately normal.
- Find the probability that the sample proportion computed from a sample of size \(900\) will be within \(5\) percentage points of the true population proportion.
Solution
- The information given is that \(p=0.38\), hence \(q=1-p=0.62\). First we use the formulas to compute the mean and standard deviation of \(\hat{p}\):
\[\mu _{\hat{p}}=p=0.38\; \text{and}\; \sigma _{\hat{P}}=\sqrt{\frac{pq}{n}}=\sqrt{\frac{(0.38)(0.62)}{900}}=0.01618 \nonumber \]
Then \(3\sigma _{\hat{P}}=3(0.01618)=0.04854\approx 0.05\) so
\[\left [ \hat{p} - 3\sqrt{\frac{\hat{p}(1-\hat{p})}{n}},\, \hat{p}+3\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \right ]=[0.38-0.05,0.38+0.05]=[0.33,0.43] \nonumber \]
which lies wholly within the interval \([0,1]\), so it is safe to assume that \(\hat{p}\) is approximately normally distributed.
- To be within \(5\) percentage points of the true population proportion \(0.38\) means to be between \(0.38-0.05=0.33\) and \(0.38+0.05=0.43\). Thus
\[\begin{align*} P(0.33<\hat{P}<0.43) &= P\left ( \frac{0.33-\mu _{\hat{P}}}{\sigma _{\hat{P}}} <Z< \frac{0.43-\mu _{\hat{P}}}{\sigma _{\hat{P}}} \right )\\[4pt] &= P\left ( \frac{0.33-0.38}{0.01618} <Z< \frac{0.43-0.38}{0.01618}\right )\\[4pt] &= P(-3.09<Z<3.09)\\[4pt] &= P(3.09)-P(-3.09)\\[4pt] &= 0.9990-0.0010\\[4pt] &= 0.9980 \end{align*} \nonumber \]
An online retailer claims that \(90\%\) of all orders are shipped within \(12\) hours of being received. A consumer group placed \(121\) orders of different sizes and at different times of day; \(102\) orders were shipped within \(12\) hours.
- Compute the sample proportion of items shipped within \(12\) hours.
- Confirm that the sample is large enough to assume that the sample proportion is normally distributed. Use \(p=0.90\), corresponding to the assumption that the retailer’s claim is valid.
- Assuming the retailer’s claim is true, find the probability that a sample of size \(121\) would produce a sample proportion so low as was observed in this sample.
- Based on the answer to part (c), draw a conclusion about the retailer’s claim.
Solution
- The sample proportion is the number \(x\) of orders that are shipped within \(12\) hours divided by the number \(n\) of orders in the sample:
\[\hat{p} =\frac{x}{n}=\frac{102}{121}=0.84\nonumber \]
- Since \(p=0.90\), \(q=1-p=0.10\), and \(n=121\),
\[\sigma _{\hat{P}}=\sqrt{\frac{(0.90)(0.10)}{121}}=0.0\overline{27}\nonumber \]
hence
\[\left [ p-3\sigma _{\hat{P}},\, p+3\sigma _{\hat{P}} \right ]=[0.90-0.08,0.90+0.08]=[0.82,0.98]\nonumber \]
Because\[[0.82,0.98]⊂[0,1]\nonumber \]
it is appropriate to use the normal distribution to compute probabilities related to the sample proportion \(\hat{P}\).
- Using the value of \(\hat{P}\) from part (a) and the computation in part (b),
\[\begin{align*} P(\hat{P}\leq 0.84) &= P\left ( Z\leq \frac{0.84-\mu _{\hat{P}}}{\sigma _{\hat{P}}} \right )\\[4pt] &= P\left ( Z\leq \frac{0.84-0.90}{0.0\overline{27}} \right )\\[4pt] &= P(Z\leq -2.20)\\[4pt] &= 0.0139 \end{align*} \nonumber \]
- The computation shows that a random sample of size \(121\) has only about a \(1.4\%\) chance of producing a sample proportion as the one that was observed, \(\hat{p} =0.84\), when taken from a population in which the actual proportion is \(0.90\). This is so unlikely that it is reasonable to conclude that the actual value of \(p\) is less than the \(90\%\) claimed.
Key Takeaway
- The sample proportion is a random variable \(\hat{P}\).
- There are formulas for the mean \(μ_{\hat{P}}\), and standard deviation \(σ_{\hat{P}}\) of the sample proportion.
- When the sample size is large the sample proportion is normally distributed.


