13.4: Facts About the F Distribution
- Page ID
- 809
Here are some facts about the \(F\) distribution:
- The curve is not symmetrical but skewed to the right.
- There is a different curve for each set of \(dfs\).
- The \(F\) statistic is greater than or equal to zero.
- As the degrees of freedom for the numerator and for the denominator get larger, the curve approximates the normal.
- Other uses for the \(F\) distribution include comparing two variances and two-way Analysis of Variance. Two-Way Analysis is beyond the scope of this chapter.
Let’s return to the slicing tomato exercise. The means of the tomato yields under the five mulching conditions are represented by \(\mu_{1}, \mu_{2}, \mu_{3}, \mu_{4}, \mu_{5}\). We will conduct a hypothesis test to determine if all means are the same or at least one is different. Using a significance level of 5%, test the null hypothesis that there is no difference in mean yields among the five groups against the alternative hypothesis that at least one mean is different from the rest.
Answer
The null and alternative hypotheses are:
- \(H_{0}: \mu_{1} = \mu_{2} = \mu_{3} = \mu_{4} = \mu_{5}\)
- \(H_{a}: \mu_{i} \neq \mu_{j}\) some \(i \neq j\)
The one-way ANOVA results are shown in Table
| Source of Variation | Sum of Squares (\(SS\)) | Degrees of Freedom (\(df\)) | Mean Square (\(MS\)) | \(F\) |
|---|---|---|---|---|
| Factor (Between) | 36,648,561 | \(5 - 1 = 4\) | \(\dfrac{36,648,561}{4} = 9,162,140\) |
\(\dfrac{9,162,140}{2,044,672.6} = 4.4810\) |
| Error (Within) | 20,446,726 | \(15 - 5 = 10\) |
\(\dfrac{20,446,726}{10} = 2,044,672.6\) |
|
| Total | 57,095,287 | \(15 - 1 = 14\) |
Distribution for the test: \(F_{4,10}\)
\[df(\text{num}) = 5 - 1 = 4\]
\[df(\text{denom}) = 15 - 5 = 10\]
Test statistic: \(F = 4.4810\)
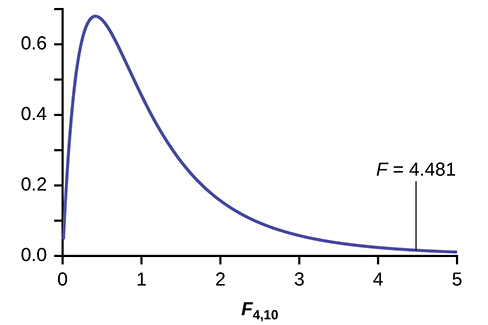
Probability Statement: \(p\text{-value} = P(F > 4.481) = 0.0248\).
Compare \(\alpha\) and the \(p\text{-value}\): \(\alpha = 0.05, p\text{-value} = 0.0248\)
Make a decision: Since \(\alpha > p\text{-value}\), we reject \(H_{0}\).
Conclusion: At the 5% significance level, we have reasonably strong evidence that differences in mean yields for slicing tomato plants grown under different mulching conditions are unlikely to be due to chance alone. We may conclude that at least some of mulches led to different mean yields.
To find these results on the calculator:
Press STAT. Press 1:EDIT. Put the data into the lists L1, L2, L3, L4, L5.
Press STAT, and arrow over to TESTS, and arrow down to ANOVA. Press ENTER, and then enter L1, L2, L3, L4, L5). Press ENTER. You will see that the values in the foregoing ANOVA table are easily produced by the calculator, including the test statistic and the p-value of the test.
The calculator displays:
- \(F = 4.4810\)
- \(p = 0.0248\) (\(p\text{-value}\))
Factor
- \(df = 4\)
- \(SS = 36648560.9\)
- \(MS = 9162140.23\)
Error
- \(df = 10\)
- \(SS = 20446726\)
- \(MS = 2044672.6\)
MRSA, or Staphylococcus aureus, can cause a serious bacterial infections in hospital patients. Table shows various colony counts from different patients who may or may not have MRSA.
| Conc = 0.6 | Conc = 0.8 | Conc = 1.0 | Conc = 1.2 | Conc = 1.4 |
|---|---|---|---|---|
| 9 | 16 | 22 | 30 | 27 |
| 66 | 93 | 147 | 199 | 168 |
| 98 | 82 | 120 | 148 | 132 |
Plot of the data for the different concentrations:

Test whether the mean number of colonies are the same or are different. Construct the ANOVA table (by hand or by using a TI-83, 83+, or 84+ calculator), find the p-value, and state your conclusion. Use a 5% significance level.
Answer
While there are differences in the spreads between the groups (Figure \(\PageIndex{1}\)), the differences do not appear to be big enough to cause concern.
We test for the equality of mean number of colonies:
\(H_{0}: \mu_{1} = \mu_{2} = \mu_{3} = \mu_{4} = \mu_{5}\)
\(H_{a}: \mu_{i} \neq \mu_{j}\) some \(i \neq j\)
The one-way ANOVA table results are shown in Table.
| Source of Variation | Sum of Squares (\(SS\)) | Degrees of Freedom (\(df\)) | Mean Square (\(MS\)) | \(F\) |
|---|---|---|---|---|
| Factor (Between) | 10,233 | \(5 - 1 = 4\) | \(\dfrac{10,233}{4} = 2,558.25\) | \(\dfrac{2,558.25}{4,194.9} = 0.6099\) |
| Error (Within) | 41,949 | \(15 - 5 = 10\) | ||
| Total | 52,182 | \(15 - 1 = 14\) | \(\dfrac{41,949}{10} = 4,194.9\) |
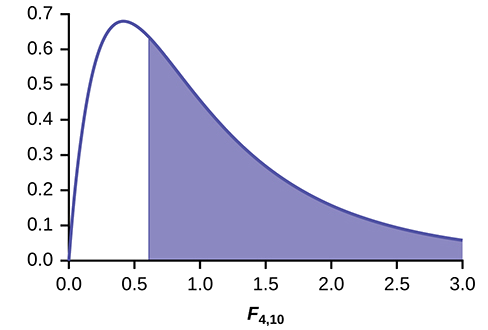
Figure \(\PageIndex{2}\)
Distribution for the test: \(F_{4,10}\)
Probability Statement: \(p\text{-value} = P(F > 0.6099) = 0.6649\).
Compare \(\alpha\) and the \(p\text{-value}\): \(\alpha = 0.05, p\text{-value} = 0.669, \alpha > p\text{-value}\)
Make a decision: Since \(\alpha > p\text{-value}\), we do not reject \(H_{0}\).
Conclusion: At the 5% significance level, there is insufficient evidence from these data that different levels of tryptone will cause a significant difference in the mean number of bacterial colonies formed.
Four sororities took a random sample of sisters regarding their grade means for the past term. The results are shown in Table.
| Sorority 1 | Sorority 2 | Sorority 3 | Sorority 4 |
|---|---|---|---|
| 2.17 | 2.63 | 2.63 | 3.79 |
| 1.85 | 1.77 | 3.78 | 3.45 |
| 2.83 | 3.25 | 4.00 | 3.08 |
| 1.69 | 1.86 | 2.55 | 2.26 |
| 3.33 | 2.21 | 2.45 | 3.18 |
Using a significance level of 1%, is there a difference in mean grades among the sororities?
Answer
Let \(\mu_{1}, \mu_{2}, \mu_{3}, \mu_{4}\) be the population means of the sororities. Remember that the null hypothesis claims that the sorority groups are from the same normal distribution. The alternate hypothesis says that at least two of the sorority groups come from populations with different normal distributions. Notice that the four sample sizes are each five.
This is an example of a balanced design, because each factor (i.e., sorority) has the same number of observations.
\(H_{0}: \mu_{1} = \mu_{2} = \mu_{3} = \mu_{4}\)
\(H_{a}\): Not all of the means \(\mu_{1}, \mu_{2}, \mu_{3}, \mu_{4}\) are equal.
Distribution for the test: \(F_{3,16}\)
where \(k = 4\) groups and \(n = 20\) samples in total
\(df(\text{num}) = k - 1 = 4 - 1 = 3\)
\(df(\text{denom}) = n - k = 20 - 4 = 16\)
Calculate the test statistic: \(F = 2.23\)
Graph:
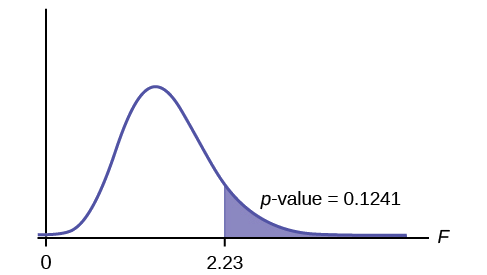
Probability statement: \(p\text{-value} = P(F > 2.23) = 0.1241\)
Compare \(\alpha\) and the \(p\text{-value}\): \(\alpha = 0.01\)
\(p\text{-value} = 0.1241\)
\(\alpha < p\text{-value}\)
Make a decision: Since \(\alpha < p\text{-value}\), you cannot reject \(H_{0}\).
Conclusion: There is not sufficient evidence to conclude that there is a difference among the mean grades for the sororities.
Put the data into lists L1, L2, L3, and L4. Press STAT and arrow over to TESTS. Arrow down to F:ANOVA. Press ENTER and Enter (L1,L2,L3,L4).
The calculator displays the F statistic, the \(p\text{-value}\) and the values for the one-way ANOVA table:
\(F = 2.2303\)
\(p = 0.1241\) (\(p\text{-value}\))
Factor
\(df = 3\)
\(SS = 2.88732\)
\(MS = 0.96244\)
Error
\(df = 1\)
\(SS = 6.9044\)
\(MS = 0.431525\)
Four sports teams took a random sample of players regarding their GPAs for the last year. The results are shown in Table.
| Basketball | Baseball | Hockey | Lacrosse |
|---|---|---|---|
| 3.6 | 2.1 | 4.0 | 2.0 |
| 2.9 | 2.6 | 2.0 | 3.6 |
| 2.5 | 3.9 | 2.6 | 3.9 |
| 3.3 | 3.1 | 3.2 | 2.7 |
| 3.8 | 3.4 | 3.2 | 2.5 |
Use a significance level of 5%, and determine if there is a difference in GPA among the teams.
Answer
With a \(p\text{-value}\) of \(0.9271\), we decline to reject the null hypothesis. There is not sufficient evidence to conclude that there is a difference among the GPAs for the sports teams.
A fourth grade class is studying the environment. One of the assignments is to grow bean plants in different soils. Tommy chose to grow his bean plants in soil found outside his classroom mixed with dryer lint. Tara chose to grow her bean plants in potting soil bought at the local nursery. Nick chose to grow his bean plants in soil from his mother's garden. No chemicals were used on the plants, only water. They were grown inside the classroom next to a large window. Each child grew five plants. At the end of the growing period, each plant was measured, producing the data (in inches) in Table \(\PageIndex{3}\).
| Tommy's Plants | Tara's Plants | Nick's Plants |
|---|---|---|
| 24 | 25 | 23 |
| 21 | 31 | 27 |
| 23 | 23 | 22 |
| 30 | 20 | 30 |
| 23 | 28 | 20 |
Does it appear that the three media in which the bean plants were grown produce the same mean height? Test at a 3% level of significance.
Answer
This time, we will perform the calculations that lead to the \(F'\) statistic. Notice that each group has the same number of plants, so we will use the formula
\[F' = \dfrac{n \cdot s_{\bar{x}}^{2}}{s^{2}_{\text{pooled}}}.\]
First, calculate the sample mean and sample variance of each group.
| Tommy's Plants | Tara's Plants | Nick's Plants | |
|---|---|---|---|
| Sample Mean | 24.2 | 25.4 | 24.4 |
| Sample Variance | 11.7 | 18.3 | 16.3 |
Next, calculate the variance of the three group means (Calculate the variance of 24.2, 25.4, and 24.4). Variance of the group means \(= 0.413 = s_{\bar{x}}^{2}\)
Then \(MS_{\text{between}} = ns_{\bar{x}}^{2} = (5)(0.413)\) where \(n = 5\) is the sample size (number of plants each child grew).
Calculate the mean of the three sample variances (Calculate the mean of 11.7, 18.3, and 16.3). Mean of the sample variances \(= 15.433 = s^{2}_{\text{pooled}}\)
Then \(MS_{\text{within}} = s^{2}_{\text{pooled}} = 15.433\).
The \(F\) statistic (or \(F\) ratio) is \(F = \dfrac{MS_{\text{between}}}{MS_{\text{within}}} = \dfrac{ns_{\bar{x}}^{2}}{s^{2}_{\text{pooled}}} = \dfrac{(5)(0.413)}{15.433} = 0.134\)
The \(dfs\) for the numerator \(= \text{the number of groups} - 1 = 3 - 1 = 2\).
The \(dfs\) for the denominator \(= \text{the total number of samples} - \text{the number of groups} = 15 - 3 = 12\)
The distribution for the test is \(F_{2,12}\) and the \(F\) statistic is \(F = 0.134\)
The \(p\text{-value}\) is \(P(F > 0.134) = 0.8759\).
Decision: Since \(\alpha = 0.03\) and the \(p\text{-value} = 0.8759\), do not reject \(H_{0}\). (Why?)
Conclusion: With a 3% level of significance, from the sample data, the evidence is not sufficient to conclude that the mean heights of the bean plants are different.
To calculate the \(p\text{-value}\):
*Press 2nd DISTR
*Arrow down to Fcdf(and press ENTER.
*Enter 0.134, E99, 2, 12)
*Press ENTER
The \(p\text{-value}\) is \(0.8759\).
Another fourth grader also grew bean plants, but this time in a jelly-like mass. The heights were (in inches) 24, 28, 25, 30, and 32. Do a one-way ANOVA test on the four groups. Are the heights of the bean plants different? Use the same method as shown in Example \(\PageIndex{3}\).
Answer
- \(F = 0.9496\)
- \(p\text{-value} = 0.4402\)
From the sample data, the evidence is not sufficient to conclude that the mean heights of the bean plants are different.
From the class, create four groups of the same size as follows: men under 22, men at least 22, women under 22, women at least 22. Have each member of each group record the number of states in the United States he or she has visited. Run an ANOVA test to determine if the average number of states visited in the four groups are the same. Test at a 1% level of significance. Use one of the solution sheets in [link].
References
- Data from a fourth grade classroom in 1994 in a private K – 12 school in San Jose, CA.
- Hand, D.J., F. Daly, A.D. Lunn, K.J. McConway, and E. Ostrowski. A Handbook of Small Datasets: Data for Fruitfly Fecundity. London: Chapman & Hall, 1994.
- Hand, D.J., F. Daly, A.D. Lunn, K.J. McConway, and E. Ostrowski. A Handbook of Small Datasets.London: Chapman & Hall, 1994, pg. 50.
- Hand, D.J., F. Daly, A.D. Lunn, K.J. McConway, and E. Ostrowski. A Handbook of Small Datasets. London: Chapman & Hall, 1994, pg. 118.
- “MLB Standings – 2012.” Available online at http://espn.go.com/mlb/standings/_/year/2012.
- Mackowiak, P. A., Wasserman, S. S., and Levine, M. M. (1992), "A Critical Appraisal of 98.6 Degrees F, the Upper Limit of the Normal Body Temperature, and Other Legacies of Carl Reinhold August Wunderlich," Journal of the American Medical Association, 268, 1578-1580.
Review
The graph of the \(F\) distribution is always positive and skewed right, though the shape can be mounded or exponential depending on the combination of numerator and denominator degrees of freedom. The \(F\) statistic is the ratio of a measure of the variation in the group means to a similar measure of the variation within the groups. If the null hypothesis is correct, then the numerator should be small compared to the denominator. A small \(F\) statistic will result, and the area under the \(F\) curve to the right will be large, representing a large \(p\text{-value}\). When the null hypothesis of equal group means is incorrect, then the numerator should be large compared to the denominator, giving a large \(F\) statistic and a small area (small \(p\text{-value}\)) to the right of the statistic under the \(F\) curve.
When the data have unequal group sizes (unbalanced data), then techniques discussed earlier need to be used for hand calculations. In the case of balanced data (the groups are the same size) however, simplified calculations based on group means and variances may be used. In practice, of course, software is usually employed in the analysis. As in any analysis, graphs of various sorts should be used in conjunction with numerical techniques. Always look of your data!


