7.1: Introduction to Normal Distributions
- Page ID
- 2117
Learning Objectives
- Describe the shape of normal distributions
- State \(7\) features of normal distributions
The normal distribution is the most important and most widely used distribution in statistics. It is sometimes called the "bell curve," although the tonal qualities of such a bell would be less than pleasing. It is also called the "Gaussian curve" after the mathematician Karl Friedrich Gauss. As you will see in the section on the history of the normal distribution, although Gauss played an important role in its history, Abraham de Moivre first discovered the normal distribution.
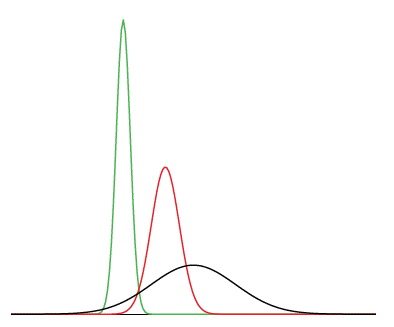
Strictly speaking, it is not correct to talk about "the normal distribution" since there are many normal distributions. Normal distributions can differ in their means and in their standard deviations. Figure \(\PageIndex{1}\) shows three normal distributions. The green (left-most) distribution has a mean of \(-3\) and a standard deviation of \(0.5\), the distribution in red (the middle distribution) has a mean of \(0\) and a standard deviation of \(1\), and the distribution in black (right-most) has a mean of \(2\) and a standard deviation of \(3\). These as well as all other normal distributions are symmetric with relatively more values at the center of the distribution and relatively few in the tails.
The density of the normal distribution (the height for a given value on the \(x\) axis) is shown below. The parameters \(\mu\) and \(\sigma\) are the mean and standard deviation, respectively, and define the normal distribution. The symbol \(e\) is the base of the natural logarithm and \(\pi\) is the constant pi.
\[\frac{1}{\sqrt{2\pi \sigma ^2}}\boldsymbol{e}^{\tfrac{-(x-\mu )^2}{2\sigma ^2}}\]
Since this is a non-mathematical treatment of statistics, do not worry if this expression confuses you. We will not be referring back to it in later sections.
Seven features of normal distributions are listed below. These features are illustrated in more detail in the remaining sections of this chapter.
- Normal distributions are symmetric around their mean
- The mean, median, and mode of a normal distribution are equal.
- The area under the normal curve is equal to \(1.0\).
- Normal distributions are denser in the center and less dense in the tails.
- Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)).
- \(68\%\) of the area of a normal distribution is within one standard deviation of the mean.
- Approximately \(95\%\) of the area of a normal distribution is within two standard deviations of the mean.


