1.12: Linear Transformations
- Page ID
- 261
Learning Objectives
- Give the formula for a linear transformation
- Determine whether a transformation is linear
- Describe what is linear about a linear transformation
Often it is necessary to transform data from one measurement scale to another. For example, you might want to convert height measured in feet to height measured in inches. Table \(\PageIndex{1}\) shows the heights of four people measured in both feet and inches. To transform feet to inches, you simply multiply by \(12\). Similarly, to transform inches to feet, you divide by \(12\).
| Feet | Inches |
|---|---|
| 5.00 | 60 |
| 6.25 | 75 |
| 5.50 | 66 |
| 5.75 | 69 |
Some conversions require that you multiply by a number and then add a second number. A good example of this is the transformation between degrees Celsius and degrees Fahrenheit. Table \(\PageIndex{2}\) shows the temperatures of five US cities in the early afternoon of \(\text{November 16, 2002}\).
| City | Degrees Fahrenheit | Degrees Celsius |
|---|---|---|
| Houston | 54 | 12.22 |
| Chicago | 37 | 2.78 |
| Minneapolis | 31 | -0.56 |
| Miami | 78 | 25.56 |
| Phoenix | 70 | 21.11 |
The formula to transform Celsius to Fahrenheit is:
\[F = 1.8C + 32\]
The formula for converting from Fahrenheit to Celsius is
\[C = 0.5556F - 17.778\]
The transformation consists of multiplying by a constant and then adding a second constant. For the conversion from Celsius to Fahrenheit, the first constant is \(1.8\) and the second is \(32\).
Figure \(\PageIndex{1}\) shows a plot of degrees Celsius as a function of degrees Fahrenheit. Notice that the points form a straight line. This will always be the case if the transformation from one scale to another consists of multiplying by one constant and then adding a second constant. Such transformations are therefore called linear transformations.
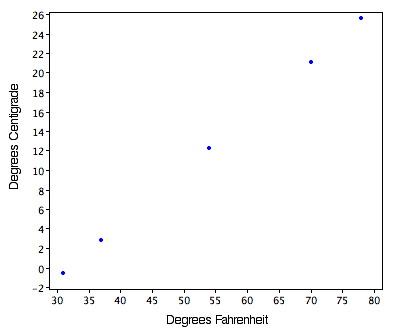
Many transformations are not linear. With nonlinear transformations, the points in a plot of the transformed variable against the original variable would not fall on a straight line. Examples of nonlinear transformations are: square root, raising to a power, logarithm, and any of the trigonometric functions.
- David M. Lane


