9.E: Sampling Distributions (Exercises)
- Page ID
- 2271
You may want to use the "r to z' calculator" and the "Calculate Area for a given X" applet for some of these exercises.
General Questions
Q1
A population has a mean of \(50\) and a standard deviation of \(6\).
- What are the mean and standard deviation of the sampling distribution of the mean for \(N = 16\)?
- What are the mean and standard deviation of the sampling distribution of the mean for \(N = 20\)? (relevant section)
Q2
Given a test that is normally distributed with a mean of \(100\) and a standard deviation of \(12\), find:
- the probability that a single score drawn at random will be greater than \(110\) ( relevant section)
- the probability that a sample of \(25\) scores will have a mean greater than \(105\) (relevant section)
- the probability that a sample of \(64\) scores will have a mean greater than \(105\) (relevant section)
- the probability that the mean of a sample of \(16\) scores will be either less than \(95\) or greater than \(105\) (relevant section)
Q3
What term refers to the standard deviation of the sampling distribution? (relevant section)
Q4
- If the standard error of the mean is \(10\) for \(N = 12\), what is the standard error of the mean for \(N = 22\)?
- If the standard error of the mean is \(50\) for \(N = 25\), what is it for \(N = 64\)? (relevant section)
Q5
A questionnaire is developed to assess women's and men's attitudes toward using animals in research. One question asks whether animal research is wrong and is answered on a \(7\)-point scale. Assume that in the population, the mean for women is \(5\), the mean for men is \(4\), and the standard deviation for both groups is \(1.5\). Assume the scores are normally distributed. If \(12\) women and \(12\) men are selected randomly, what is the probability that the mean of the women will be more than \(1.5\) points higher than the mean of the men? (relevant section)
Q6
If the correlation between reading achievement and math achievement in the population of fifth graders were \(0.60\), what would be the probability that in a sample of \(28\) students, the sample correlation coefficient would be greater than \(0.65\)? (relevant section)
Q7
If numerous samples of \(N = 15\) are taken from a uniform distribution and a relative frequency distribution of the means is drawn, what would be the shape of the frequency distribution? (relevant section & relevant section)
Q8
A normal distribution has a mean of \(20\) and a standard deviation of \(10\). Two scores are sampled randomly from the distribution and the second score is subtracted from the first. What is the probability that the difference score will be greater than \(5\)? Hint: Read the Variance Sum Law section of Chapter 3. (relevant section & relevant section)
Q9
What is the shape of the sampling distribution of \(r\)? In what way does the shape depend on the size of the population correlation? (relevant section)
Q10
If you sample one number from a standard normal distribution, what is the probability it will be \(0.5\)? (relevant section & relevant section)
Q11
A variable is normally distributed with a mean of \(120\) and a standard deviation of \(5\). Four scores are randomly sampled. What is the probability that the mean of the four scores is above \(127\)? (relevant section)
Q12
The correlation between self esteem and extraversion is \(0.30\). A sample of \(84\) is taken.
- What is the probability that the correlation will be less than \(0.10\)?
- What is the probability that the correlation will be greater than \(0.25\)? (relevant section)
Q13
The mean GPA for students in \(\text{School A}\) is \(3.0\); the mean GPA for students in \(\text{School B}\) is \(2.8\). The standard deviation in both schools is \(0.25\). The GPAs of both schools are normally distributed. If \(9\) students are randomly sampled from each school, what is the probability that:
- the sample mean for \(\text{School A}\) will exceed that of \(\text{School A}\) by \(0.5\) or more? (relevant section)
- the sample mean for \(\text{School B}\) will be greater than the sample mean for \(\text{School A}\)? (relevant section)
Q14
In a city, \(70\%\) of the people prefer \(\text{Candidate A}\). Suppose \(30\) people from this city were sampled.
- What is the mean of the sampling distribution of \(p\)?
- What is the standard error of \(p\)?
- What is the probability that \(80\%\) or more of this sample will prefer \(\text{Candidate A}\)?
- What is the probability that \(45\%\) or more of this sample will prefer some other candidate? (relevant section)
Q15
When solving problems where you need the sampling distribution of \(r\), what is the reason for converting from \(r\) to \(z'\)? (relevant section)
Q16
In the population, the mean SAT score is \(1000\). Would you be more likely (or equally likely) to get a sample mean of \(1200\) if you randomly sampled \(10\) students or if you randomly sampled \(30\) students? Explain. (relevant section & relevant section)
Q17
True/false: The standard error of the mean is smaller when \(N = 20\) than when \(N = 10\). (relevant section)
Q18
True/false: The sampling distribution of \(r =0.8\) becomes normal as \(N\) increases. (relevant section)
Q19
True/false: You choose \(20\) students from the population and calculate the mean of their test scores. You repeat this process \(100\) times and plot the distribution of the means. In this case, the sample size is \(100\). (relevant section & relevant section)
Q20
True/false: In your school, \(40\%\) of students watch TV at night. You randomly ask \(5\) students every day if they watch TV at night. Every day, you would find that \(2\) of the \(5\) do watch TV at night. (relevant section & relevant section)
Q21
True/false: The median has a sampling distribution. (relevant section)
Q22
True/false: Refer to the figure below. The population distribution is shown in black, and its corresponding sampling distribution of the mean for \(N = 10\) is labeled "\(A\)" (relevant section & relevant section)
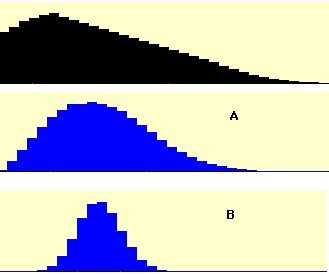
Questions from Case Studies
The following questions use data from the Angry Moods (AM) case study.
Q23
- How many men were sampled?
- How many women were sampled?
Q24
What is the mean difference between men and women on the Anger-Out scores?
Q25
Suppose in the population, the Anger-Out score for men is two points higher than it is for women. The population variances for men and women are both \(20\). Assume the Anger-Out scores for both genders are normally distributed. Given this information about the population parameters:
- What is the mean of the sampling distribution of the difference between means? (relevant section)
- What is the standard error of the difference between means? (relevant section)
- What is the probability that you would have gotten this mean difference (see #24) or less in your sample? (relevant section)
The following questions use data from the Animal Research (AR) case study.
Q26
How many people were sampled to give their opinions on animal research?
Q27
(AR#11) What is the correlation in this sample between the belief that animal research is wrong and belief that animal research is necessary? (Ch. 4.E)
Q28
Suppose the correlation between the belief that animal research is wrong and the belief that animal research is necessary is \(-0.68\) in the population.
- Convert \(-0.68\) to \(z'\). (relevant section)
- Find the standard error of this sampling distribution. (relevant section)
- In a new sample, what is the probability that you would get the correlation found in the original sample (see #27) or a lower correlation (closer to \(-1\))? (relevant section)
Selected Answers
S1
- Mean = \(50\), SD = \(1.5\)
S2
- \(0.019\)
S4
- \(7.39\)
S11
\(0.0026\)
S12
- \(0.690\)
S13
- \(0.0055\)
S14
- \(0.116\)
S23
- \(30\)
S25
- \(2\)
S28
- \(0.603\)


