9.7: Sampling Distribution of Pearson's r
- Page ID
- 2268
Learning Objectives
- Transform \(r\) to \(z'\)
- Calculate the probability of obtaining an \(r\) above a specified value
Assume that the correlation between quantitative and verbal SAT scores in a given population is \(0.60\). In other words, \(\rho =0.60\). If \(12\) students were sampled randomly, the sample correlation, \(r\), would not be exactly equal to \(0.60\). Naturally different samples of \(12\) students would yield different values of \(r\). The distribution of values of \(r\) after repeated samples of \(12\) students is the sampling distribution of \(r\).
The shape of the sampling distribution of \(r\) for the above example is shown in Figure \(\PageIndex{1}\). You can see that the sampling distribution is not symmetric: it is negatively skewed. The reason for the skew is that \(r\) cannot take on values greater than \(1.0\) and therefore the distribution cannot extend as far in the positive direction as it can in the negative direction. The greater the value of \(\rho\), the more pronounced the skew.
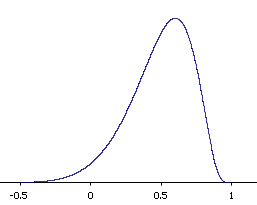
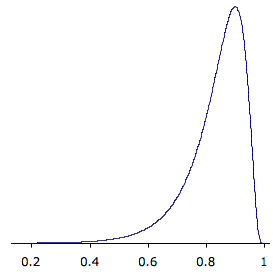
Figure \(\PageIndex{2}\) shows the sampling distribution for \(\rho =0.90\). This distribution has a very short positive tail and a long negative tail.
Referring back to the SAT example, suppose you wanted to know the probability that in a sample of \(12\) students, the sample value of \(r\) would be \(0.75\) or higher. You might think that all you would need to know to compute this probability is the mean and standard error of the sampling distribution of \(r\). However, since the sampling distribution is not normal, you would still not be able to solve the problem. Fortunately, the statistician Fisher developed a way to transform \(r\) to a variable that is normally distributed with a known standard error. The variable is called \(z'\) and the formula for the transformation is given below.
\[z' = 0.5\: \ln \frac{1+r}{1-r}\]
The details of the formula are not important here since normally you will use either a table, Pearson r to Fisher z' or calculator to do the transformation. What is important is that \(z'\) is normally distributed and has a standard error of
\[\frac{1}{\sqrt{N-3}}\]
where \(N\) is the number of pairs of scores.
Example \(\PageIndex{1}\)
Let's return to the question of determining the probability of getting a sample correlation of \(0.75\) or above in a sample of \(12\) from a population with a correlation of \(0.60\).
Solution
The first step is to convert both \(0.60\) and \(0.75\) to their \(z'\) values, which are \(0.693\) and \(0.973\), respectively.
The standard error of \(z'\) for \(N = 12\) is \(0.333\).
Therefore the question is reduced to the following: given a normal distribution with a mean of \(0.693\) and a standard deviation of \(0.333\), what is the probability of obtaining a value of \(0.973\) or higher?
The answer can be found directly from the applet "Calculate Area for a given X" to be \(0.20\).
Alternatively, you could use the formula:
\[z = \frac{X - \mu }{\sigma } = \frac{0.973 - 0.693}{0.333} = 0.841\]
and use a table to find that the area above \(0.841\) is \(0.20\).


