7.7: Normal Approximation Demonstration
- Page ID
- 2397
Learning Objectives
- State the relationship between sample size and the accuracy of normal approximation of the binomial distribution
Instructions
The normal distribution can be used to approximate the binomial distribution. This demonstration allows you to explore the accuracy of the approximation under a variety of conditions.
Illustrated Instructions
The demonstration displays the probability of success over a specific number of trials based on the entered total number of trials (\(N\)) and the probability of success on a given trial. You can change \(N\) as well as \(p\) and then select the proportion for which you would like the probability to be calculated.
By clicking the appropriate radio button, you can choose to calculate the probability above a specified value or between two values. Try out various values of \(N\) and \(p\) to calculate various approximations to the binomial to explore the accuracy of the approximation.
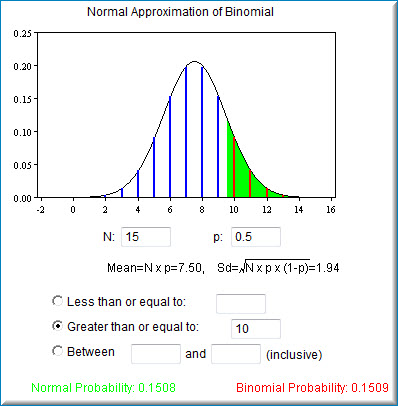
The calculation based on the normal approximation to the binomial is shown in green below and is equal to \(0.1714\). The actual binomial probability of \(0.1719\) is shown in red.

The screenshot below displays results for the probability of greater than \(10\) successful trials with \(15\) total trials and a \(0.5\) probability of success. The probability based on the normal approximation is displayed at the bottom of the screen in green next to the binomial probability displayed in red.