7.2: History of the Normal Distribution
- Page ID
- 2118
Learning Objectives
- Learn the interesting history of a normal curve
In the chapter on probability, we saw that the binomial distribution could be used to solve problems such as "If a fair coin is flipped \(100\) times, what is the probability of getting \(60\) or more heads?" The probability of exactly \(x\) heads out of \(N\) flips is computed using the formula:
\[P(x)=\frac{N!}{x!(N-x)!}\pi ^x(1-\pi )^{N-x}\]
where \(x\) is the number of heads (\(60\)), \(N\) is the number of flips (\(100\)), and \(\pi\) is the probability of a head (\(0.5\)). Therefore, to solve this problem, you compute the probability of \(60\) heads, then the probability of \(61\) heads, \(62\) heads, etc., and add up all these probabilities. Imagine how long it must have taken to compute binomial probabilities before the advent of calculators and computers.
Abraham de Moivre, an \(18^{th}\) century statistician and consultant to gamblers, was often called upon to make these lengthy computations. de Moivre noted that when the number of events (coin flips) increased, the shape of the binomial distribution approached a very smooth curve. Binomial distributions for \(2\), \(4\), and \(12\) flips are shown in Figure \(\PageIndex{1}\).
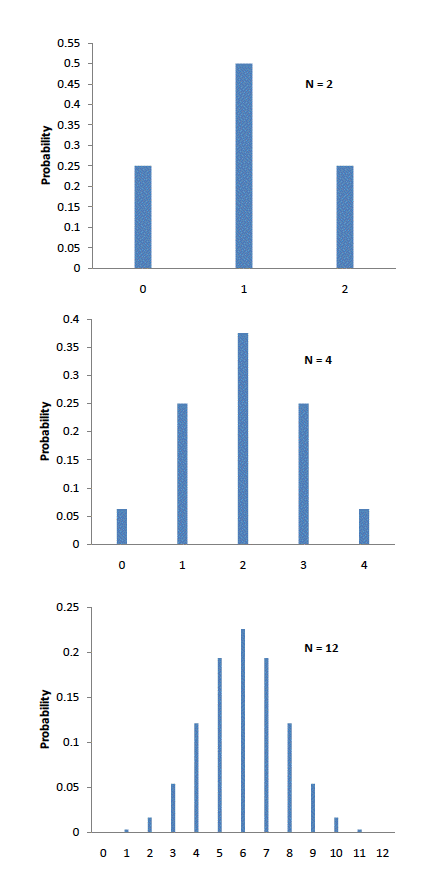
de Moivre reasoned that if he could find a mathematical expression for this curve, he would be able to solve problems such as finding the probability of \(60\) or more heads out of \(100\) coin flips much more easily. This is exactly what he did, and the curve he discovered is now called the "normal curve."
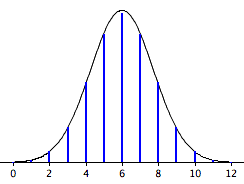
The smooth curve in Figure \(\PageIndex{2}\) is the normal distribution. Note how well it approximates the binomial probabilities represented by the heights of the blue lines.
The importance of the normal curve stems primarily from the fact that the distributions of many natural phenomena are at least approximately normally distributed. One of the first applications of the normal distribution was to the analysis of errors of measurement made in astronomical observations, errors that occurred because of imperfect instruments and imperfect observers. Galileo in the \(17^{th}\) century noted that these errors were symmetric and that small errors occurred more frequently than large errors. This led to several hypothesized distributions of errors, but it was not until the early \(19^{th}\) century that it was discovered that these errors followed a normal distribution. Independently, the mathematicians Adrain in \(1808\) and Gauss in \(1809\) developed the formula for the normal distribution and showed that errors were fit well by this distribution.
This same distribution had been discovered by Laplace in \(1778\) when he derived the extremely important central limit theorem, the topic of a later section of this chapter. Laplace showed that even if a distribution is not normally distributed, the means of repeated samples from the distribution would be very nearly normally distributed, and that the larger the sample size, the closer the distribution of means would be to a normal distribution.
Most statistical procedures for testing differences between means assume normal distributions. Because the distribution of means is very close to normal, these tests work well even if the original distribution is only roughly normal.
Quételet was the first to apply the normal distribution to human characteristics. He noted that characteristics such as height, weight, and strength were normally distributed.


