5.4: Rule of Complement

Last updated
Save as PDF

Page ID: 20880

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

It is sometimes difficult to calculate the probability that an event will occur, but it is much easier to calculate the probability that an event will not occur.

For example you may want to determine the probability that a student at California State University – East Bay majors in something other than Business. Instead of adding up all the non‐Business major probabilities, it would be much easier to find the chance that a student at CSUEB majors in Business, say 21%. Then you would determine that the probability that a student does not major in Business (all other students) is the remaining 79%.

Rule of Complement

A'(read as “A‐complement”) is the event that event A does not occur. In that case, the Rule of Complement is:

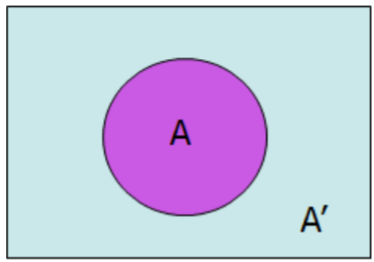
\[P(A)+P\left(A^{\prime}\right)=1 \quad P(A)=1-P\left(A^{\prime}\right) \quad P\left(A^{\prime}\right)=1-P(A) \nonumber \]

Example: Die rolling

In a game, you must keep rolling a six‐sided die until you get a six. What is the probability that you would need 2 or more rolls to get a six?

Solution

The event A is “2 or more rolls to get a six” which would be a very difficult probability to calculate ‐‐ it’s actually an infinite sum!

The event A’ is “do not take 2 or more rolls to get a six” which is the same as saying “get a six on the first roll.” That’s a much easier probability to calculate, \(P\left(A^{\prime}\right)=1 / 6\).

So \(P(A)=1-P\left(A^{\prime}\right)=1-1 / 6=5 / 6\)

Therefore, the probability of needing two or more rolls to get a six is 5/6 or about 83.3%