3.3: The PACF of a Causal ARMA Process
- Page ID
- 873
In this section, the partial autocorrelation function (PACF) is introduced to further assess the dependence structure of stationary processes in general and causal ARMA processes in particular. To start with, let us compute the ACVF of a moving average process of order \(q\)
Example \(\PageIndex{1}\): The ACVF of an MA(\(q\)) process
Let \((X_t\colon t\in\mathbb{Z})\) be an MA(\(q\)) process specified by the polynomial \(\theta(z)=1+\theta_1z+\ldots+\theta_qz^q\). Then, letting \(\theta_0=1\), it holds that
\[ E[X_t]=\sum_{j=0}^q\theta_jE[Z_{t-j}]=0. \nonumber \]
Solution
To compute the ACVF, suppose that \(h\geq 0\) and write
\begin{align*}
\gamma(h)&= Cov(X_{t+h},X_{t})=E[X_{t+h}X_{t}]\\[.2cm]
&=E\left[\left(\sum_{j=0}^q\theta_jZ_{t+h-j}\right)
\left(\sum_{k=0}^q\theta_kZ_{t-k}\right)\right]\\[.2cm]
&=\sum_{j=0}^q\sum_{k=0}^q\theta_j\theta_kE[Z_{t+h-j}Z_{t-k}]\\[.2cm]
&=\left\{\begin{array}{l@{\qquad}r}
\displaystyle\sigma^2\sum_{k=0}^{q-h}\theta_{k+h}\theta_k,
& 0\leq h\leq q.\\[.2cm]
0, & h>q.
\end{array}\right.
\end{align*}
The result here is a generalization of the MA(1) case, which was treated in Example 3.2.3. It is also a special case of the linear process in Example 3.1.4. The structure of the ACVF for MA processes indicates a possible strategy to determine in practice the unknown order \(q\): plot the the sample ACF and select as order \(q\) the largest lag such that \(\rho(h)\) is significantly different from zero.
While the sample ACF can potentially reveal the true order of an MA process, the same is not true anymore in the case of AR processes. Even for the AR(1) time series it has been shown in Example 3.2.1 that its ACF \(\rho(h)=\phi^{|h|}\) is nonzero for all lags. As further motivation, however, we discuss the following example.
Example 3.3.2
Let \((X_t\colon t\in\mathbb{Z})\) be a causal AR(1) process with parameter \(|\phi|<1\). It holds that
\[ \gamma(2)=Cov(X_2,X_{0})
=Cov(\phi^2X_{0}+\phi Z_{1}+Z_2,X_{0})
=\phi^2\gamma(0)\not=0. \nonumber \]
To break the linear dependence between \(X_0\) and \(X_2\), subtract \(\phi X_1\) from both variables. Calculating the resulting covariance yields
\[ Cov(X_2-\phi X_{1},X_0-\phi X_1)= Cov(Z_2,X_0-\phi X_1)=0, \nonumber \]
since, due to the causality of this AR(1) process, \(X_0-\phi X_1\) is a function of \(Z_{1},Z_0,Z_{-1},\ldots\) and therefore uncorrelated with \(X_2-\phi X_1=Z_2\).
The previous example motivates the following general definition.
Definition 3.3.1 Partial autocorrelation function
Let \((X_t\colon t\in\mathbb{Z})\) be a weakly stationary stochastic process with zero mean. Then, the sequence \((\phi_{hh}\colon h\in\mathbb{N})\) given by
\begin{align*}
\phi_{11}&=\rho(1)=Corr(X_1,X_0), \\[.2cm]
\phi_{hh}&=Corr(X_h-X_h^{h-1},X_0-X_0^{h-1}), \qquad
h\geq 2,
\end{align*}
is called the partial autocorrelation function (PACF) of \((X_t\colon t\in\mathbb{Z})\).
Therein,
\begin{align*}
X_h^{h-1}&=\mbox{regression of $X_h$ on
}(X_{h-1},\ldots,X_1)\\[.2cm]
&=\beta_1X_{h-1}+\beta_2X_{h-2}+\ldots+\beta_{h-1}X_1 \\[.3cm]
X_0^{h-1}&=\mbox{regression of $X_0$ on
}(X_1,\ldots,X_{h-1})\\[.2cm]
&=\beta_1X_1+\beta_2X_2+\ldots+\beta_{h-1}X_{h-1}.
\end{align*}
Notice that there is no intercept coefficient \(\beta_0\) in the regression parameters, since it is assumed that \(E[X_t]=0\). The following example demonstrates how to calculate the regression parameters in the case of an AR(1) process.
Example 3.3.3 PACF of an AR(1) process]
If \((X_t\colon t\in\mathbb{Z})\) is a causal AR(1) process, then \(\phi_{11}=\rho(1)=\phi\). To calculate \(\phi_{22}\), calculate first \(X_2^1=\beta X_1\), that is \(\beta\). This coefficient is determined by minimizing the mean-squared error between \(X_2\) and \(\beta X_1\):
\[ E[X_2-\beta X_1]^2=\gamma(0)-2\beta\gamma(1)+\beta^2\gamma(0) \nonumber \]
which is minimized by \(\beta=\rho(1)=\phi\). (This follows easily by taking the derivative and setting it to zero.) Therefore \(X_2^1=\phi X_1\). Similarly, one computes \(X_0^1=\phi X_1\) and it follows from Example 3.3.2 that \(\phi_{22}=0\). Indeed all lags \(h\geq 2\) of the PACF are zero.
More generally, consider briefly a causal AR(\(p\)) process given by \(\phi(B)X_t=Z_t\) with \(\phi(z)=1-\phi_1z-\ldots-\phi_pz^p\).
Then, for \(h>p\),
\[ X_h^{h-1}=\sum_{j=1}^p\phi_jX_{h-j} \nonumber \]
and consequently
\[ \phi_{hh}=Corr(X_h-X_h^{h-1},X_0-X_0^{h-1}) = Corr(Z_h,X_0-X_0^{h-1})=0 \nonumber \]
if \(h>p\) by causality (the same argument used in Example 3.3.2 applies here as well). Observe, however, that \(\phi_{hh}\) is not necessarily zero if \(h\leq p\). The forgoing suggests that the sample version of the PACF can be utilized to identify the order of an autoregressive process from data: use as \(p\) the largest lag \(h\) such that \(\phi_{hh}\) is significantly different from zero.
On the other hand, for an invertible MA(\(q\)) process, one can write \(Z_t=\pi(B)X_t\) or, equivalently,
\[ X_t=-\sum_{j=1}^\infty\pi_jX_{t-j}+Z_t \nonumber \]
which shows that the PACF of an MA(\(q\)) process will be nonzero for all lags, since for a ``perfect'' regression one would have to use all past variables \((X_s\colon s<t)\) instead of only the quantity \(X_t^{t-1}\) given in Definition 3.3.1.
In summary, the PACF reverses the behavior of the ACVF for autoregressive and moving average processes. While the latter have an ACVF that vanishes after lag \(q\) and a PACF that is nonzero (though decaying) for all lags, AR processes have an ACVF that is nonzero (though decaying) for all lags but a PACF that vanishes after lag \(p\).
ACVF (ACF) and PACF hence provide useful tools in assessing the dependence of given ARMA processes. If the estimated ACVF (the estimated PACF) is essentially zero after some time lag, then the underlying time series can be conveniently modeled with an MA (AR) process---and no general ARMA sequence has to be fitted. These conclusions are summarized in Table 3.3.1
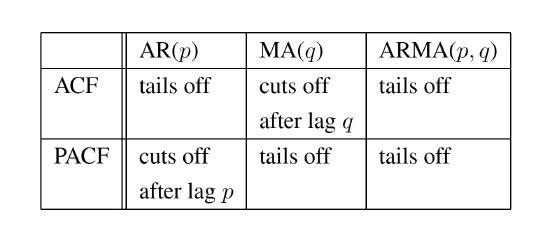
Table 3.1: The behavior of ACF and PACF for AR, MA, and ARMA processes.
Example 3.3.4
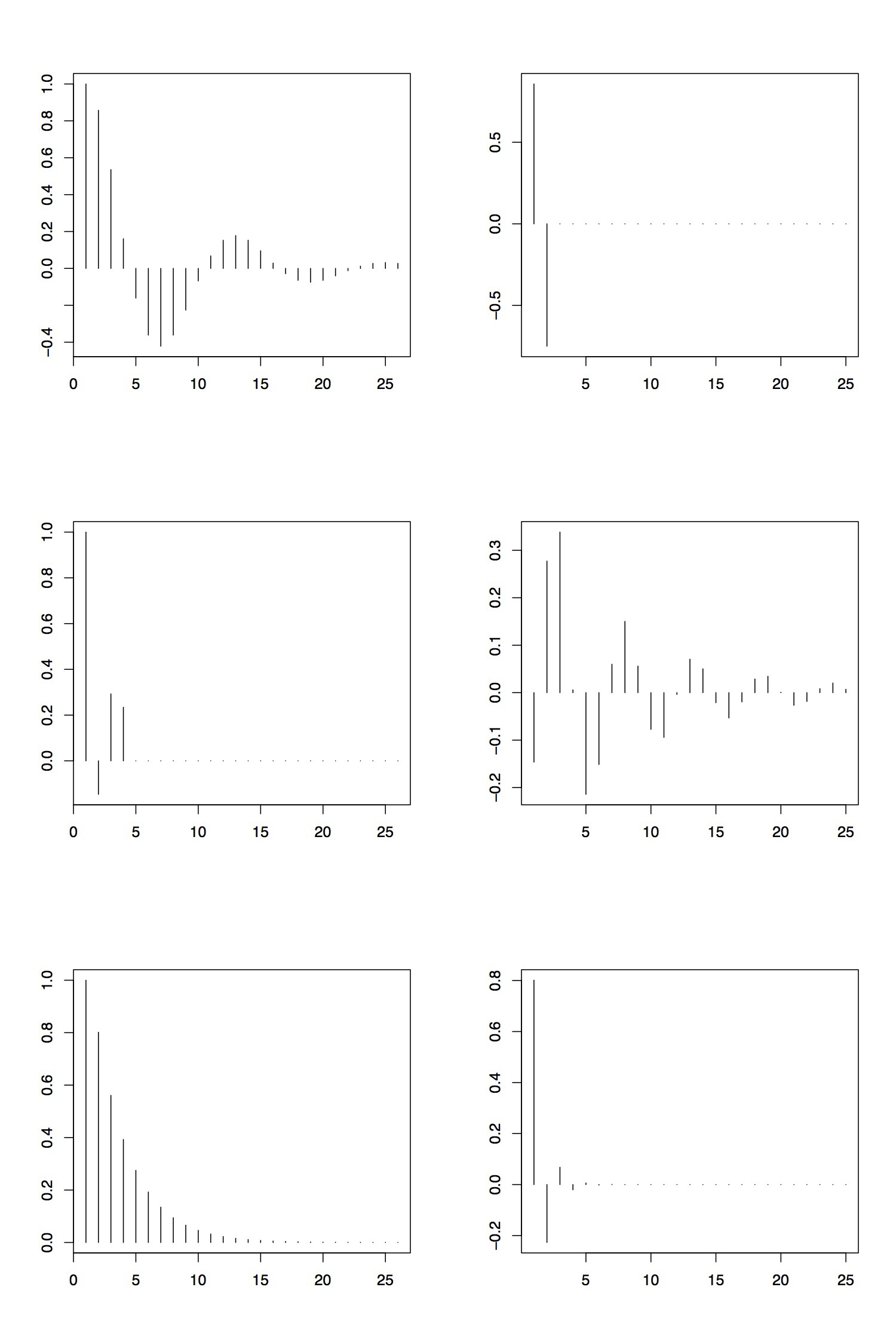
Figure 3.5 collects the ACFs and PACFs of three ARMA processes. The upper panel is taken from the AR(2) process with parameters \(\phi_1=1.5\) and \(\phi_2=-.75\). It can be seen that the ACF tails off and displays cyclical behavior (note that the corresponding autoregressive polynomial has complex roots). The PACF, however, cuts off after lag 2. Thus, inspecting ACF and PACF, we would correctly specify the order of the AR process.
The middle panel shows the ACF and PACF of the MA(3) process given by the parameters \(\theta_1=1.5\), \(\theta_2=-.75\) and \(\theta_3=3\). The plots confirm that \(q=3\) because the ACF cuts off after lag 3 and the PACF tails off.
Finally, the lower panel displays the ACF and PACF of the ARMA(1,1) process of Example 3.2.4. Here, the assessment is much harder. While the ACF tails off as predicted (see Table 3.1), the PACF basically cuts off after lag 4 or 5. This could lead to the wrong conclusion that the underlying process is actually an AR process of order 4 or 5. (The reason for this behavior lies in the fact that the dependence in this particular ARMA(1,1) process can be well approximated by that of an AR(4) or AR(5) time series.)
To reproduce the graphs in R, you can use the commands
>ar2.acf=ARMAacf(ar=c(1.5,-.75), ma=0, 25)
>ar2.pacf=ARMAacf(ar=c(1.5,-.75), ma=0, 25, pacf=T)
for the AR(2) process. The other two cases follow from straightforward adaptations of this code.
Example 3.3.5 Recruitment Series
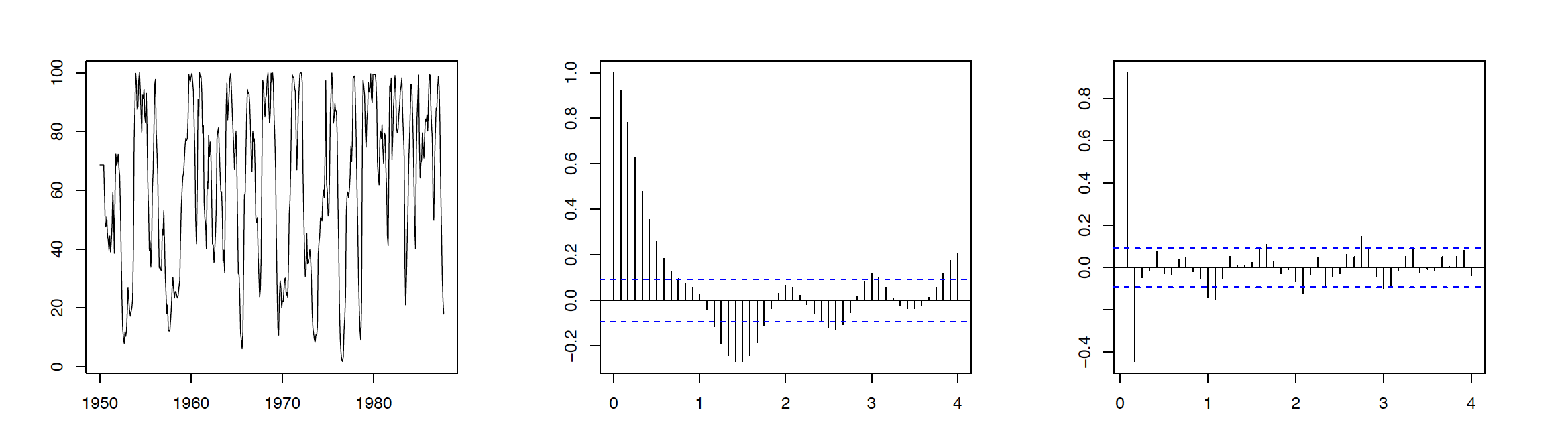
The data considered in this example consists of 453 months of observed recruitment (number of new fish) in a certain part of the Pacific Ocean collected over the years 1950--1987. The corresponding time series plot is given in the left panel of Figure 3.6. The corresponding ACF and PACF displayed in the middle and right panel of the same figure recommend fitting an AR process of order \(p=2\) to the recruitment data. Assuming that the data is in rec, the R code to reproduce Figure 3.6 is
> rec = ts(rec, start=1950, frequency=12)
> plot(rec, xlab="", ylab="")
> acf(rec, lag=48)
> pacf(rec, lag=48)
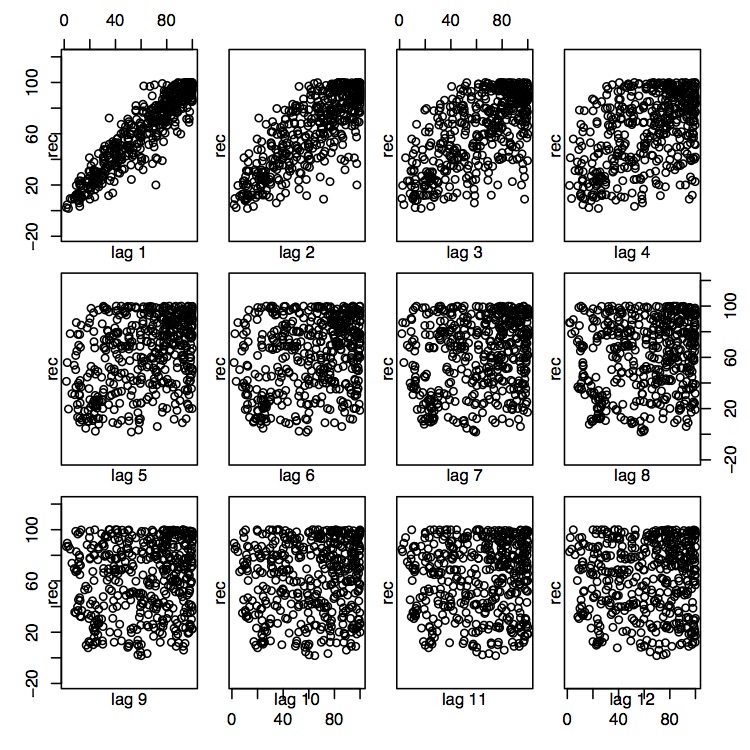
This assertion is also consistent with the scatterplots that relate current recruitment to past recruitment at several time lags, namely \(h=1,\ldots,12\). For lag 1 and 2, there seems to be a strong linear relationship, while this is not the case anymore for \(h\geq 3\). The corresponding R commands are
> lag.plot(rec, lags=12, layout=c(3,4), diag=F)
Denote by \(X_t\) the recruitment at time \(t\). To estimate the AR(2) parameters, run a regression on the observed data triplets included in the set \( (x_t,x_ t-1,x_ t-2)\colon j=3,\ldots,453 \) to fit a model of the form
\[ X_t=\phi_0+\phi_1X_ t-1+\phi_2X_ t-2+Z_t, \qquad t=3,\ldots,453, \nonumber \]
where \((Z_t)\sim\mathrm WN(0,\sigma^2)\). This task can be performed in R as follows.
> fit.rec = ar.ols(rec, aic=F, order.max=2, demean=F, intercept=T)
These estimates can be assessed with the command {\tt fit.rec} and the corresponding standard errors with \(\tt fit.rec{\$}asy.se\). Here the parameter estimates \(\hat{\phi}_0=6.737(1.111)\), \(\hat{\phi}_1=1.3541(.042)\), \(\hat{\phi}_2=-.4632(.0412)\) and \(\hat{\sigma}^2=89.72\) are obtained. The standard errors are given in parentheses.


