15.1: OLS Error Assumptions Revisited
- Page ID
- 7272
As described in earlier chapters, there is a set of key assumptions that must be met to justify the use of the tt and FF distributions in the interpretation of OLS model results. In particular, these assumptions are necessary for hypotheses tests and the generation of confidence intervals. When met, the assumptions make OLS more efficient than any other unbiased estimator.
OLS Assumptions
Systematic Component
- Linearity
- Fixed XX
Stochastic Component
- Errors have constant variance across the range of XX
E(ϵ2i)=σ2ϵE(ϵi2)=σϵ2
- Errors are independent of XX and other ϵiϵi
E(ϵi)≡E(ϵ|xi)=0E(ϵi)≡E(ϵ|xi)=0
and
E(ϵi)≠E(ϵj)E(ϵi)≠E(ϵj) for i≠ji≠j
- Errors are normally distributed
ϵi∼N(0,σ2ϵ)ϵi∼N(0,σϵ2)
There is an additional set of assumptions needed for “correct” model specification. An ideal model OLS would have the following characteristics: - YY is a linear function of modeled XX variables - No XX’s are omitted that affect E(Y)E(Y) and that are correlated with included XX’s. Note that exclusion of other XXs that are related to YY, but are not related to the XXs in the model, does not critically undermine the model estimates. However, it does reduce the overall ability to explain YY. All XX’s in the model affect E(Y)E(Y).
Note that if we omit an XX that is related to YY and other XXs in the model, we will bias the estimate of the included XXs. Also consider the problem of including XXs that are related to other XXs in the model, but not related to YY. This scenario would reduce the independent variance in XX used to predict YY.
Table 15.1 summarizes the various classes of assumption failures and their implications.
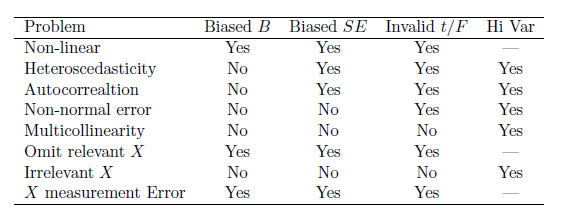
When considering the assumptions, our data permit empirical tests for some assumptions, but not all. Specifically, we can check for linearity, normality of the residuals, homoscedasticity, data “outliers” and multicollinearity. However, we can’t check for correlation between error and XX’s, whether the mean error equals zero, and whether all the relevant XX’s are included.


