1.3: Theory and Functions
- Page ID
- 7204
Closely related to hypothesis testing in empirical research is the concept of functional relationships – or functions. Hypotheses posit systematic relationships between variables, and those relationships are expressed as functions. For example, we can hypothesize that an individual’s productivity is related to coffee consumption (productivity is a function of coffee consumption).2
Functions are ubiquitous. When we perceive relational order or patterns in the world around us, we are observing functions. Individual decisions about when to cross the street, whether to take a nap or engage in a barroom brawl can all be ascribed to patterns (the walk" light was lit; someone stayed up too late last night; a Longhorn insulted the Sooner football team). Patterns are how we make sense of the world, and patterns are expressed as functions. That does not mean the functions we perceive are always correct, or that they allow us to predict perfectly. However, without functions we don’t know what to expect; chaos prevails.
In mathematical terms, a function relates an outcome variable, y, to one or more inputs, x. This can be expressed more generally as: y=f(x1,x2,x3,...xn)y=f(x1,x2,x3,...xn), which means y is a function of the x’s, or, y varies as a function of the x’s.
Functions form the basis of the statistical models that will be developed throughout the text. In particular, this text will focus on linear regression, which is based on linear functions such as y=f(x)=5+x, where 5 is a constant and x is a variable. We can plot this function with the values of x ranging from −5 to 5. This is shown in Figure \(\PageIndex{1}\).
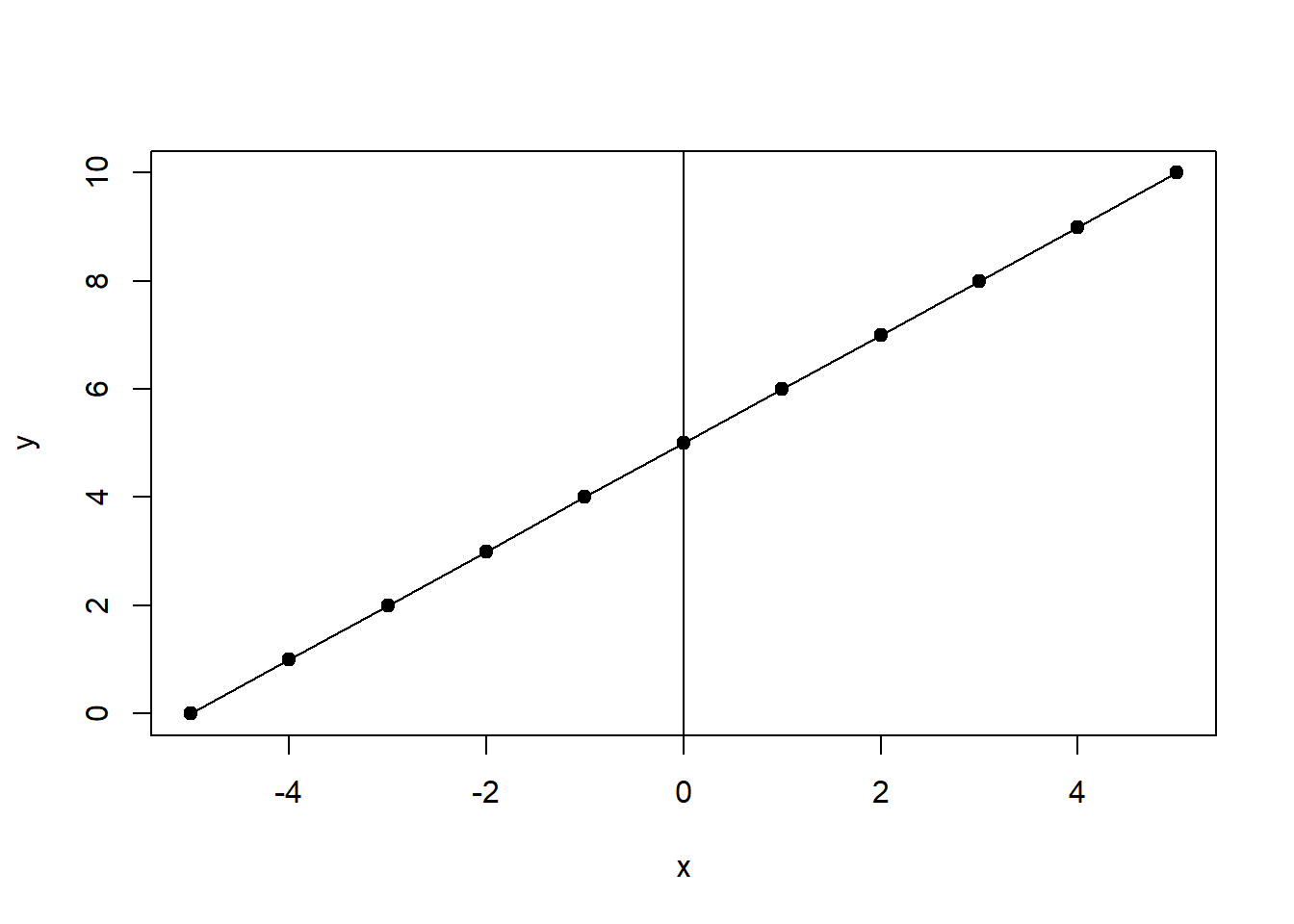
As you can see, the xx values range from −5 to 5 and the corresponding y values range from 0 to 10. The function produces a straight line because the changes in y are consistent across all values of x. This type of function is the basis of the linear models we will develop, therefore these models are said to have a linear functional form.
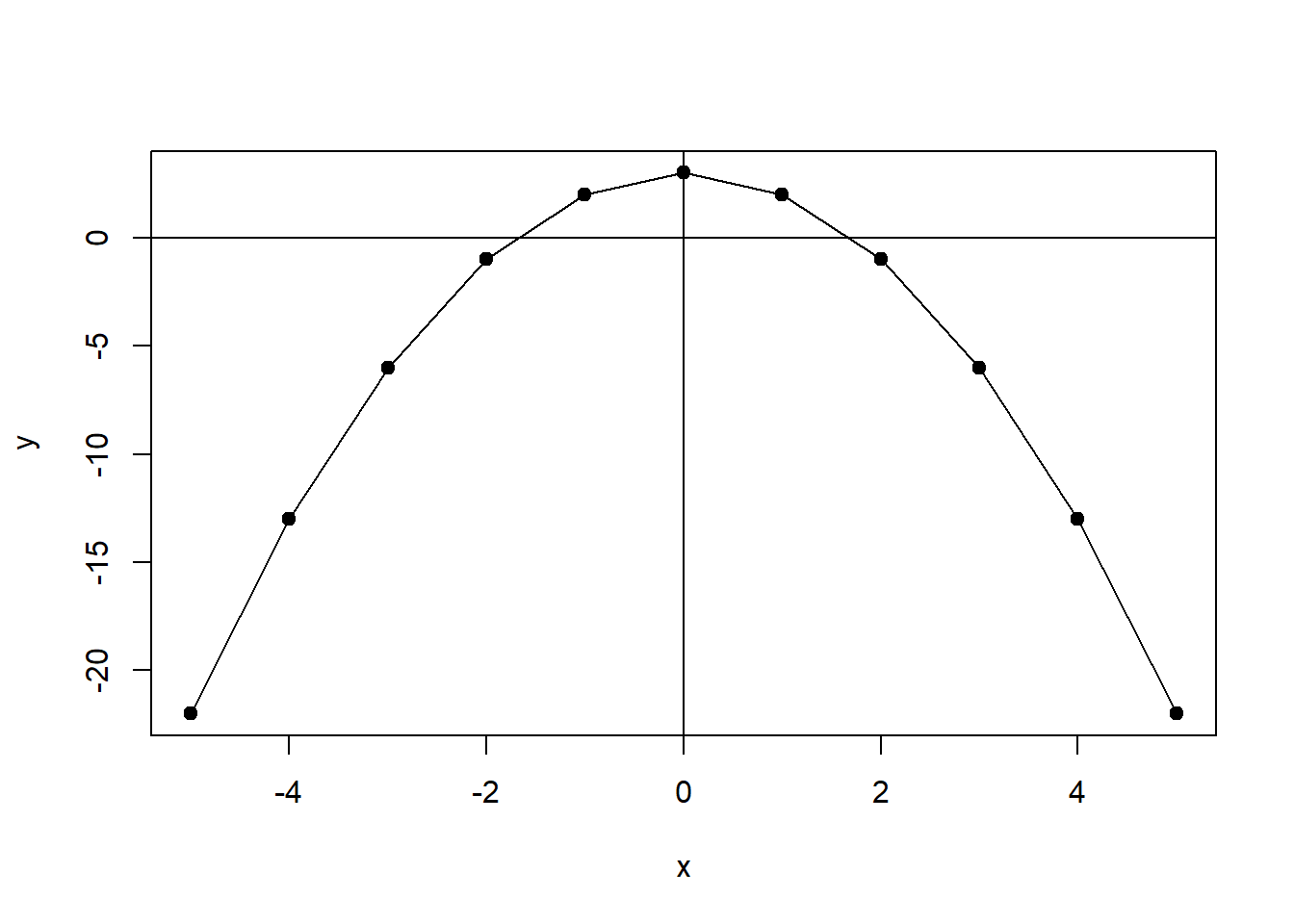
However, non-linear functional forms are also common. For example, y=f(x)=3−x2 is a quadratic function, which is a type of polynomial function since it contains a square term (an exponent). It is plotted in Figure \(\PageIndex{2}\). This function is non-linear because the changes in y are not consistent across the full range of x.
Examples of Functions in Social Science Theories
As noted, functions are the basis of statistical models that are used to test hypotheses. Below are a few examples of functions that are related to social science theories.
- Welfare and work incentives
- Employment =f(welfare programs, education level, work experience,…)
- Nuclear weapons proliferation
- Decision to develop nuclear weapons =f(perceived threat, incentives, sanctions,…)
- Priming and political campaign contributions
- Contribution($) =f(Prime (suggested $), income,…)
- Successful program implementation
- Implementation =f(clarity of law, level of public support, problem complexity,…)
Try your hand at this with theories that are familiar to you. First, identify the dependent and independent variables of interest; then develop your own conjectures about the form of the functional relationship(s) among them.


