7.2: Estimating Linear Models
- Page ID
- 7236
With stochastic models we don’t know if the error assumptions are met, nor do we know the values of αα and ββ; therefore we must estimate them, as denoted by a hat (e.g., ^αα^ is the estimate for αα). The stochastic model as shown in Equation (7.4) is estimated as:
Yi=^α+^βXi+ϵi(7.4)(7.4)Yi=α^+β^Xi+ϵi
where ϵiϵi is the residual term or the estimated error term. Since no line can perfectly pass through all the data points, we introduce a residual, ϵϵ, into the regression equation. Note that the predicted value of YY is denoted ^YY^ (yy-hat).
Yi=^α+^βXi+ϵi=^Yi+ϵiϵi=Yi−^Yi=Yi−^α−^βXiYi=α^+β^Xi+ϵi=Yi^+ϵiϵi=Yi−Yi^=Yi−α^−β^Xi
7.2.1 Residuals
Residuals measure prediction errors of how far observation YiYi is from predicted ^YiYi^. This is shown in Figure \(\PageIndex{3}\).
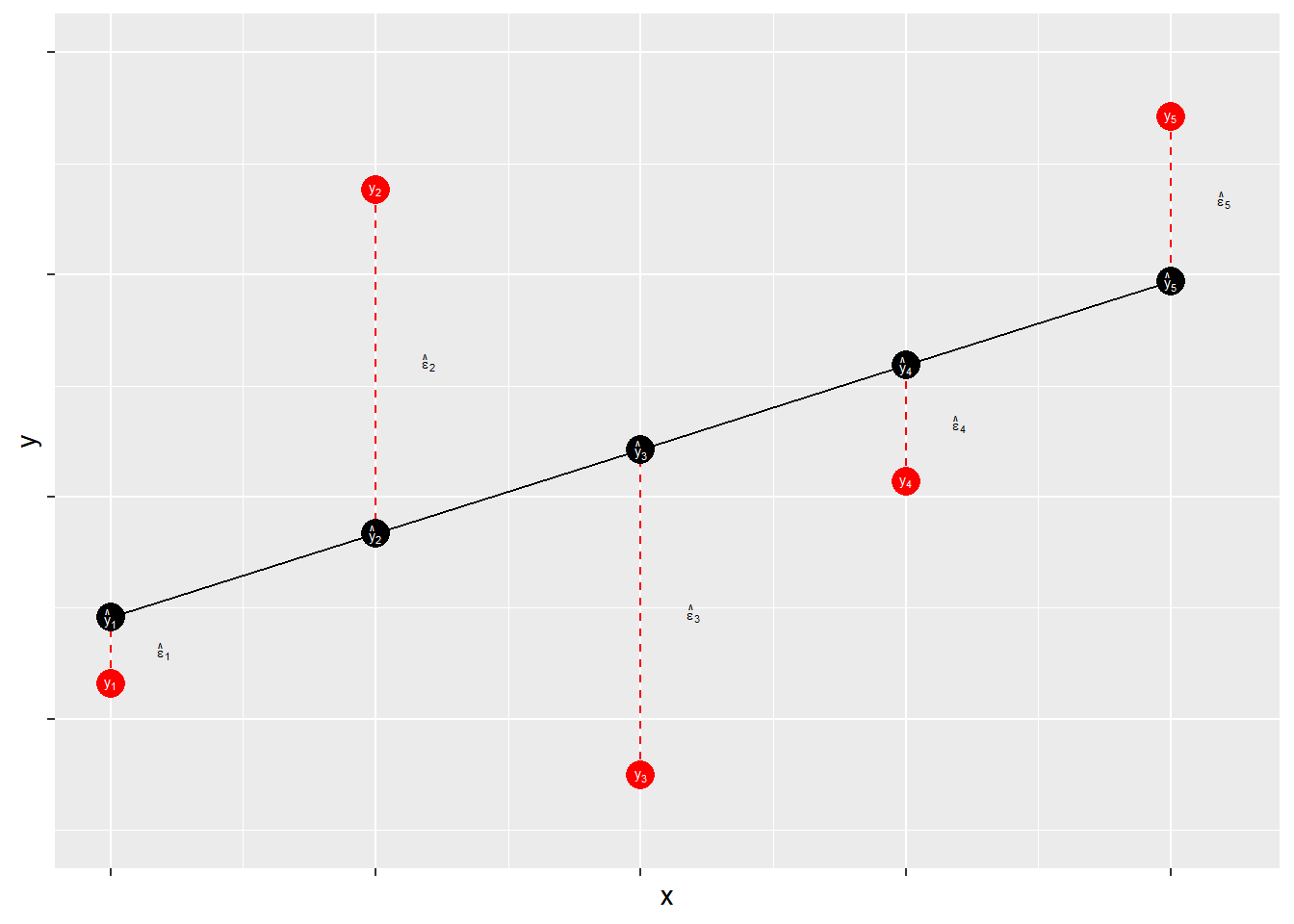
The residual term contains the accumulation (sum) of errors that can result from measurement issues, modeling problems, and irreducible randomness. Ideally, the residual term contains lots of small and independent influences that result in an overall random quality of the distribution of the errors. When that distribution is not random – that is, when the distribution of error has some systematic quality – the estimates of ^αα^ and ^ββ^ may be biased. Thus, when we evaluate our models we will focus on the shape of the distribution of our errors.
What’s in ϵϵ?
Measurement Error
- Imperfect operationalizations
- Imperfect measure application
Modeling Error
- Modeling error/mis-specification
- Missing model explanation
- Incorrect assumptions about associations
- Incorrect assumptions about distributions
Stochastic “noise”
- Unpredictable variability in the dependent variable
The goal of regression analysis is to minimize the error associated with the model estimates. As noted, the residual term is the estimated error, or overall miss" (e.g., Yi−^YiYi−Yi^). Specifically, the goal is to minimize the sum of the squared errors, ∑ϵ2∑ϵ2. Therefore, we need to find the values of ^αα^ and ^ββ^ that minimize ∑ϵ2∑ϵ2.
Note that for a fixed set of data {^αα^,^αα^}, each possible choice of values for ^αα^ and ^ββ^ corresponds to a specific residual sum of squares, ∑ϵ2∑ϵ2. This can be expressed by the following functional form:
S(^α,^β)=n∑i=1ϵ2i=∑(Yi−^Yi)2=∑(Yi−^α−^βXi)2(7.5)(7.5)S(α^,β^)=∑i=1nϵi2=∑(Yi−Yi^)2=∑(Yi−α^−β^Xi)2
Minimizing this function requires specifying estimators for ^αα^ and ^ββ^ such that S(^α,^β)=∑ϵ2S(α^,β^)=∑ϵ2 is at the lowest possible value. Finding this minimum value requires the use of calculus, which will be discussed in the next chapter. Before that, we walk through a quick example of simple regression


