9.2: Site Index
- Page ID
- 2926
Site Index
Site is defined by the Society of American Foresters (1971) as “an area considered in terms of its own environment, particularly as this determines the type and quality of the vegetation the area can carry.” Forest and natural resource managers use site measurement to identify the potential productivity of a forest stand and to provide a comparative frame of reference for management options. The productive potential or capacity of a site is often referred to as site quality.
Site quality can be measured directly or indirectly. Direct measurement of a stand’s productivity can be measured by analyzing the variables such as soil nutrients, moisture, temperature regimes, available light, slope, and aspect. A productivity-estimation method based on the permanent features of soil and topography can be used on any site and is suitable in areas where forest stands do not presently exist. Soil site index is an example of such an index. However, such indices are location specific and should not be used outside the geographic region in which they were developed. Unfortunately, environmental factor information is not always available and natural resource managers must use alternative methods.
Historical yield records also provide direct evidence of a site’s productivity by averaging the yields over multiple rotations or cutting cycles. Unfortunately, there are limited long-term data available, and yields may be affected by species composition, stand density, pests, rotation age, and genetics. Consequently, indirect methods of measuring site quality are frequently used, with the most common involving the relationship between tree height and tree age.
Using stand height data is an easy and reliable way to quantify site quality. Theoretically, height growth is sensitive to differences in site quality and height development of larger trees in an even-aged stand is seldom affected by stand density. Additionally, the volume-production potential is strongly correlated with height-growth rate. This measure of site quality is called site index and is the average total height of selected dominant-codominant trees on a site at a particular reference or index age. If you measure a stand that is at an index age, the average height of the dominant and codominant trees is the site index. It is the most widely accepted quantitative measure of site quality in the United States for even-aged stands (Avery and Burkhart 1994).
The objective of the site index method is to select the height development pattern that the stand can be expected to follow during the remainder of its life (not to predict stand height at the index age). Most height-based methods of site quality evaluation use site index curves. Site index curves are a family of height development patterns referenced by either age at breast height or total age. For example, site index curves for plantations are generally based on total age (years since planted), where age at breast height is frequently used for natural stands for the sake of convenience. If total age were to be used in this situation, the number of years required for a tree to grow from a seedling to DBH must be added in. Site index curves can either be anamorphic or polymorphic curves. Anamorphic curves (most common) are a family of curves with the same shape but different intercepts. Polymorphic curves are a family of curves with different shapes and intercepts.
The index age for this method is typically the culmination of mean annual growth. In the western part of the United States, 100 years is commonly used as the reference age with 50 years in the eastern part of this country. However, site index curves can be based on any index age that is needed. Coile and Schumacher (1964) created a family of anamorphic site index curves for plantation loblolly pine with an index age of 25 years. The following family of anamorphic site index curves for a southern pine is based on a reference age of 50 years.
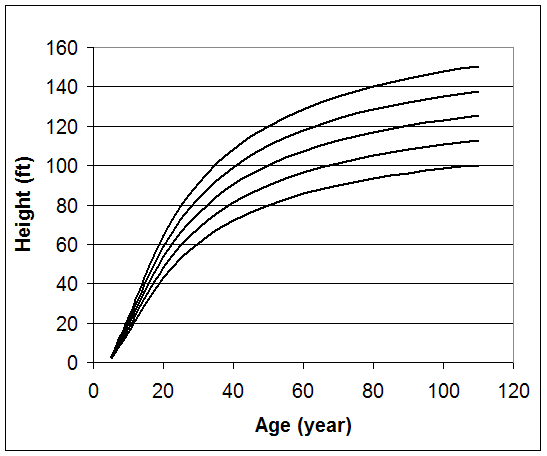
Figure 1. Site index curves with an index age of 50 years.
Creating a site index curve involves the random selection of dominant and codominant trees, measuring their total height, and statistically fitting the data to a mathematical equation. So, which equation do you use? Plotting height over age for single species, even-aged stands typically results in a sigmoid shaped pattern.
\[H_d = b_0e^{(b_1A^{-1})}\]
where Hd is the height of dominant and codominant trees, A is stand age, and b0 and b1 are coefficients to be estimated. Variable transformation is needed if linear regression is to be used to fit the model. A common transformation is
\[ln \ H_d = b_0+b_1A^{-1}\]
Coile and Schumacher (1964) fit their data to the following model:
\[ln \ S = ln \ H +5.190(\frac {1}{A} - \frac {1}{25})\]
where S is site index, H is total tree height, and A is average age. The site index curve is created by fitting the model to data from stands of varying site qualities and ages, making sure that all necessary site index classes are equally represented at all ages. It is important not to bias the curve by using an incomplete range of data.
Data for the development of site index equations can come from measurement of tree or stand height and age from temporary or permanent inventory plots or from stem analysis. Inventory plot data are typically used for anamorphic curves only and sampling bias can occur when poor sites are over represented in older age classes. Stem analysis can be used for polymorphic curves but requires destructive sampling and it can be expensive to obtain such data.
We are going to examine three different methods for developing site index equations:
- Guide curve method
- Difference equation method
- Parameter prediction method
Guide Curve Method
The guide curve method is commonly used to generate anamorphic site index equations. Let’s begin with a commonly used model form:
\[ ln \ H_d =b_0 +b_1A^{-1} = b_0 + b_1\frac{1}{A}\]
Parameterizing this model results in a “guide curve” (the average line for the sample data) that is used to create the individual height/age development curves that parallel the guide curve. For a particular site index the equation is:
\[ln \ H_d = b_{0i} +b_1A^{-1}\]
where boi is the unique y-intercept for that age. By definition, when A = A0 (index age), H is equal to site index S. Thus:
\[b_{0i} = ln \ S - b_1A_0^{-1}\]
Substituting boi into equation 9.2.5 gives:
which can be used to generate site index curves for given values of S and A0 and a range of ages (A). The equation can be algebraically rearranged as:
\[ln \ S = ln \ H -b_1(A^{-1} - A_0^{-1}) = ln (H) - b_1(\frac {1}{A} - \frac {1}{A_0})\]
This is the form to estimate site index (height at index age) when height and age data measurements are given. This process is sound only if the average site quality in the sample data is approximately the same for all age classes. If the average site quality varies systematically with age, the guide curve will be biased.
Difference Equation Method
This method requires either monumented plot, tree remeasurement data, or stem analysis data. The model is fit using differences of height and specific ages. This method is appropriate for anamorphic and polymorphic curves, especially for longer and/or multiple measurement periods. Schumacher (after Clutter et al. 1983) used this approach when estimating site index using the reciprocal of age and the natural log of height. He believed that there was a linear relationship between Point A (1/A1, lnH1) and Point B (1/A2, lnH2) and defined β1 (slope) as:
\[\beta_1 = \dfrac {ln(H_2) - ln (H_1)}{(1/A_2)-(1/A_1)}\]
where H1 and A1 were initial height and age, and H2 and A2 were height and age at the end of the remeasurement period. His height/age model became:
\[ln (H_2) = ln (H_1) +\beta_1 (\frac {1}{A_2} - \frac {1}{A_1})\]
Using remeasurement data, this equation would be fitted using linear regression procedures with the model
\[Y = \beta_1X\]
where Y = ln(H2) – ln(H1)
X = (1/A2) – (1/A1)
After estimating β1, a site index equation is obtained from the height/age equation by letting A2equal A0 (the index age) so that H2 is, by definition, site index (S). The equation can then be written:
\[ln (S) = ln(H_1) + \beta_1(\frac {1}{A_0} - \frac {1}{A_1})\]
Parameter Prediction Method
This method requires remeasurement or stem analysis data, and involves the following steps:
- Fitting a linear or nonlinear height/age function to the data on a tree-by-tree (stem analysis data) or plot by plot (remeasurement data) basis
- Using each fitted curve to assign a site index value to each tree or plot (put A0 in the equation to estimate site index)
- Relating the parameters of the fitted curves to site index through linear or nonlinear regression procedures
Trousdell et al. (1974) used this approach to estimate site index for loblolly pine and it provides an example using the Chapman-Richards (Richards 1959) function for the height/age relationship. They collected stem analysis data on 44 dominant and codominant trees that had a minimum age of at least 50 years. The Chapman-Richards function was used to define the height/age relationship:
\[H = \theta_1[1-e^{(-\theta_2A)}]^{[(1-\theta_3)^{-1}]}\]
where H is height in feet at age A and θ1, θ2, and θ3 are parameters to be estimated. This equation was fitted separately to each tree. The fitted curves were all solved with A = 50 to obtain site index values (S) for each tree.
The parameters θ1, θ2, and θ3 were hypothesized to be functions of site index, where
\[\theta_1 = \beta_1 + \beta_2S\]
\[\theta_2 = \beta_3 + \beta_4S+\beta_5S^2\]
\[\theta_3 = \beta_6 + \beta_7S + \beta_8S^2\]
The Chapman-Richards function was then expressed as:
\[H = (\beta_1+\beta_2S){1-e^{[-(\beta_3+\beta_4S+\beta_5S^2)A]}}^{[(1-\beta_6-\beta_7S-\beta_8S^2)^{-1}]}\]
This function was then refitted to the data to estimate the parameters β1, β2, …β8. The estimating equations obtained for θ1, θ2, and θ3 were
\[\hat {\theta_1} = 63.1415+0.635080S\]
\[\hat {\theta_2} = 0.00643041 + 0.000124189S + 0.00000162545S^2 \nonumber \]
\[\hat {\theta_3} = 0.0172714 - 0.00291877S + 0.0000310915S^2 \nonumber \]
For any given site index value, these equations can be solved to give a particular Chapman-Richards site index curve. By substituting various values of age into the equation and solving for H, we obtain height/age points that can be plotted for a site index curve. Since each site index curve has different parameter values, the curves are polymorphic.
Periodic Height Growth Data
An alternative to using current stand height as the surrogate for site quality is to use periodic height growth data, which is referred to as a growth intercept method. This method is practical only for species that display distinct annual branch whorls and is primarily used for juvenile stands because site index curves are less dependable for young stands.
This method requires the length measurement of a specified number of successive annual internodes or the length over a 5-year period. While the growth-intercept values can be used directly as measures of site quality, they are more commonly used to estimate site index.
Alban (1972) created a simple linear model to predict site index for red pine using 5-year growth intercept in feet beginning at 8 ft. above ground.
SI = 32.54 + 3.43 X
where SI is site index at a base age of 50 years and X is 5-year growth intercept in feet.
Using periodic height growth data has the advantage of not requiring stand age or total tree height measurements, which can be difficult in young, dense stands. However, due to the short-term nature of the data, weather variation may strongly influence the internodal growth thereby rendering the results inaccurate.
Site index equations should be based on biological or mathematical theories, which will help the equation perform better. They should behave logically and not allow unreasonable values for predicted height, especially at very young or very old ages. The equations should also contain an asymptotic parameter to control unbounded height growth at old age. The asymptote should be some function of site index such that the asymptote increases with increases of site index.
When using site index, it is important to know the base age for the curve before use. It is also important to realize that site index based on one base age cannot be converted to another base age. Additionally, similar site indices for different species do not mean similar sites even when the same base age is used for both species. You have to understand how height and age were measured before you can safely interpret a site index curve. Site index is not a true measure of site quality; rather it is a measure of a tree growth component that is affected by site quality (top height is a measure of stand development, NOT site quality).


