8.2: Software Solution
- Page ID
- 2919
Model Development and Selection
There are many different reasons for creating a multiple linear regression model and its purpose directly influences how the model is created. Listed below are several of the more commons uses for a regression model:
- Describing the behavior of your response variable
- Predicting a response or estimating the average response
- Estimating the parameters (β0, β1, β2, …)
- Developing an accurate model of the process
Depending on your objective for creating a regression model, your methodology may vary when it comes to variable selection, retention, and elimination.
When the object is simple description of your response variable, you are typically less concerned about eliminating non-significant variables. The best representation of the response variable, in terms of minimal residual sums of squares, is the full model, which includes all predictor variables available from the data set. It is less important that the variables are causally related or that the model is realistic.
A common reason for creating a regression model is for prediction and estimating. A researcher wants to be able to define events within the x-space of data that were collected for this model, and it is assumed that the system will continue to function as it did when the data were collected. Any measurable predictor variables that contain information on the response variable should be included. For this reason, non-significant variables may be retained in the model. However, regression equations with fewer variables are easier to use and have an economic advantage in terms of data collection. Additionally, there is a greater confidence attached to models that contain only significant variables.
If the objective is to estimate the model parameters, you will be more cautious when considering variable elimination. You want to avoid introducing a bias by removing a variable that has predictive information about the response. However, there is a statistical advantage in terms of reduced variance of the parameter estimates if variables truly unrelated to the response variable are removed.
Building a realistic model of the process you are studying is often a primary goal of much research. It is important to identify the variables that are linked to the response through some causal relationship. While you can identify which variables have a strong correlation with the response, this only serves as an indicator of which variables require further study. The principal objective is to develop a model whose functional form realistically reflects the behavior of a system.
The following figure is a strategy for building a regression model.
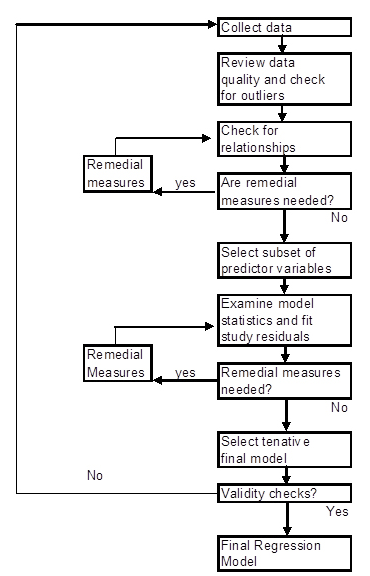
Figure \(\PageIndex{1}\) . Strategy for building a regression model.
Software Solutions
Minitab
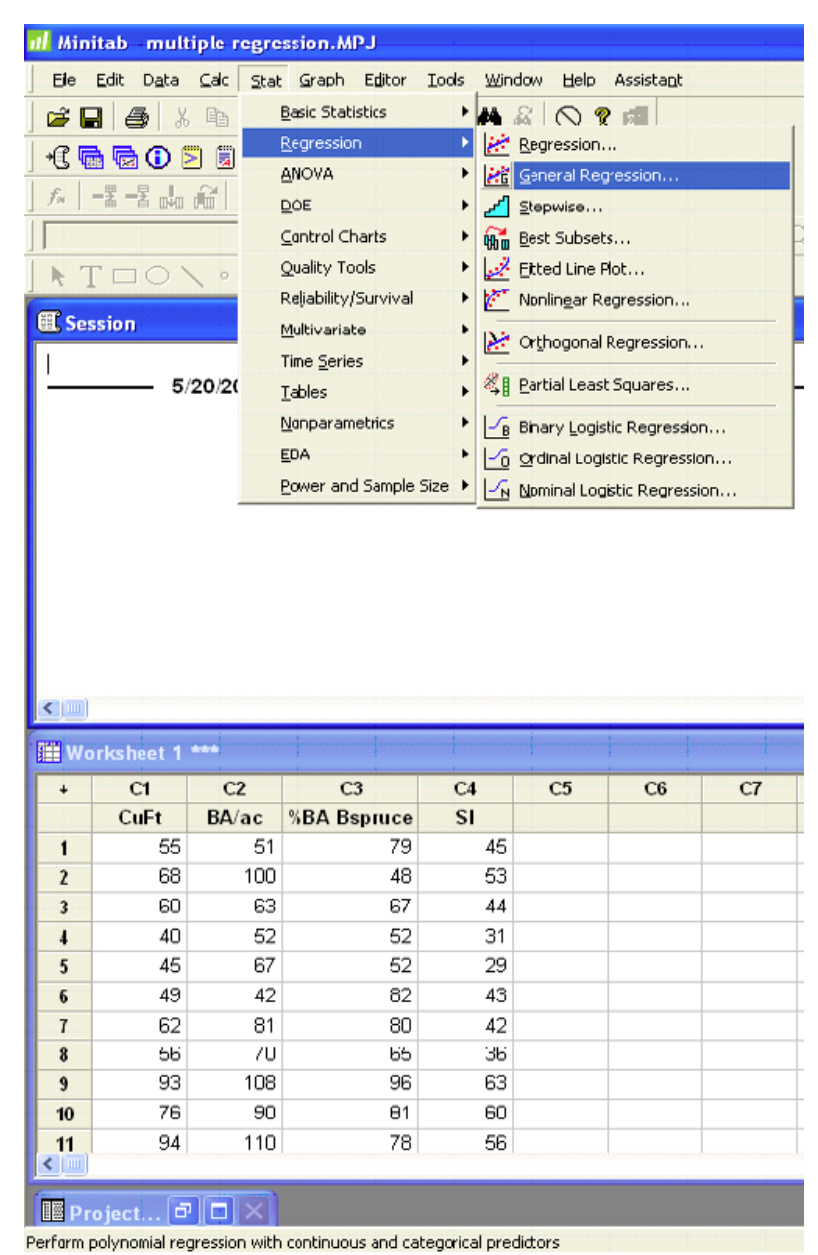
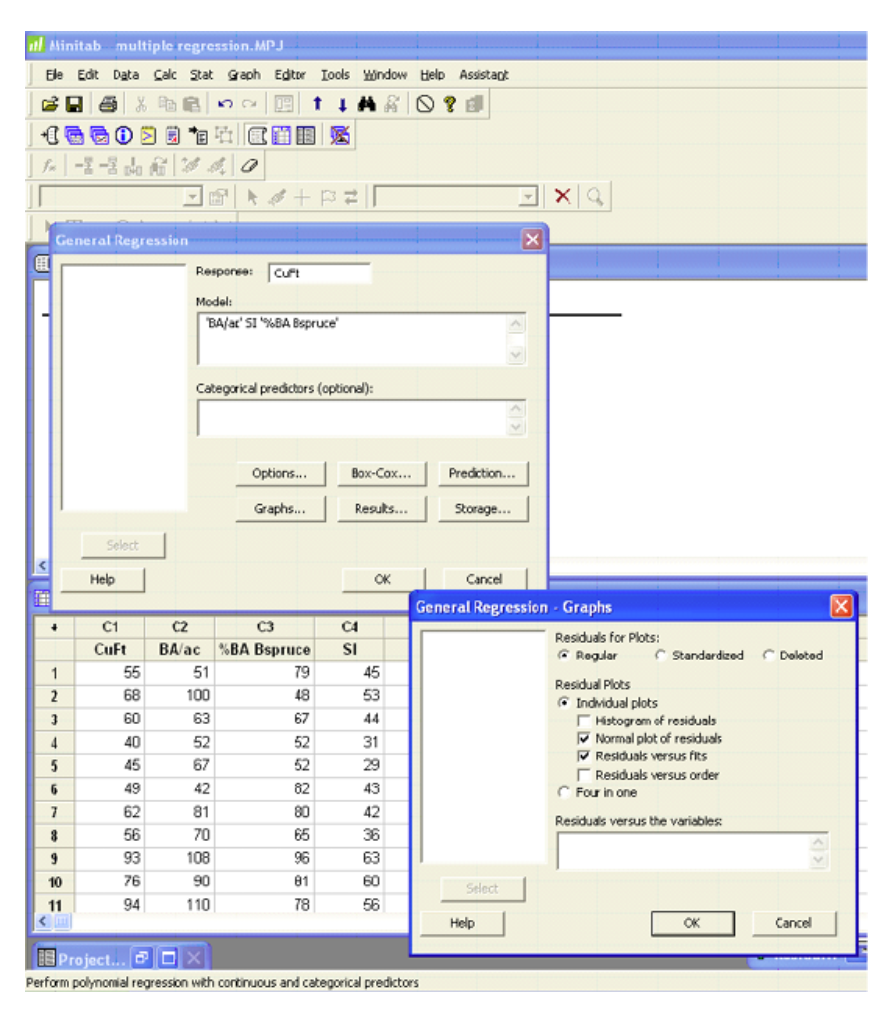
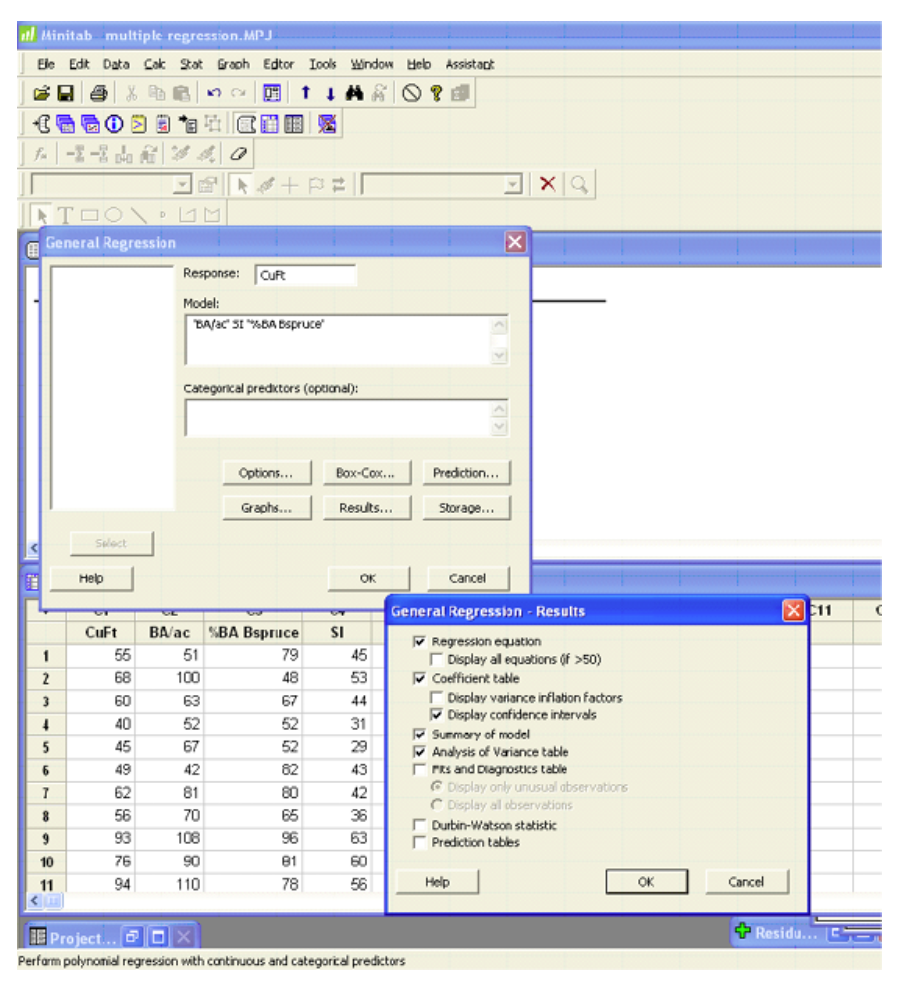
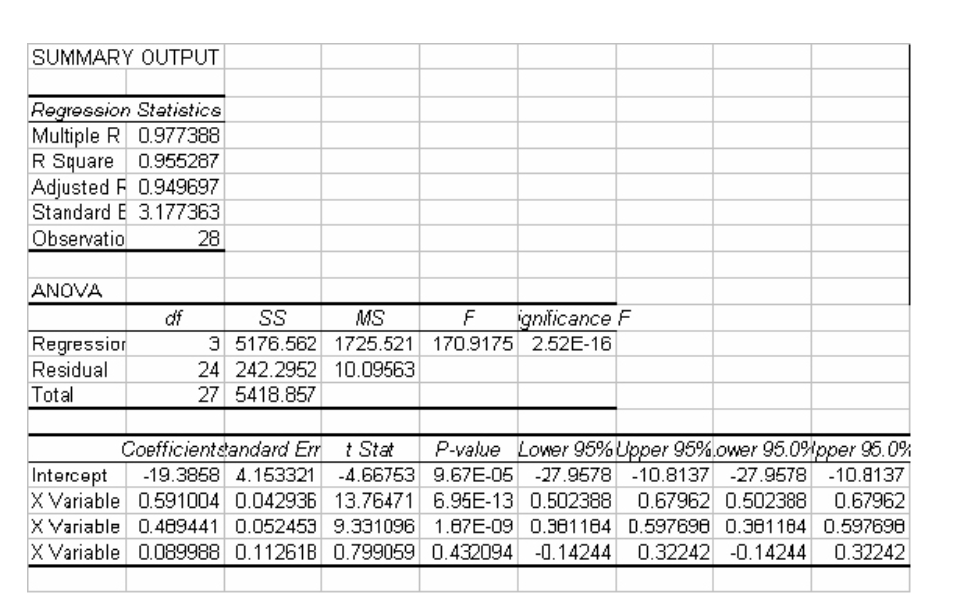
The output and plots are given in the previous example.
Excel