11.4: Making Decisions

Last updated
Save as PDF

Page ID: 4010

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Okay, we’re very close to being finished. We’ve constructed a test statistic (X), and we chose this test statistic in such a way that we’re pretty confident that if X is close to N/2 then we should retain the null, and if not we should reject it. The question that remains is this: exactly which values of the test statistic should we associate with the null hypothesis, and which exactly values go with the alternative hypothesis? In my ESP study, for example, I’ve observed a value of X=62. What decision should I make? Should I choose to believe the null hypothesis, or the alternative hypothesis?

Critical regions and critical values

To answer this question, we need to introduce the concept of a critical region for the test statistic X. The critical region of the test corresponds to those values of X that would lead us to reject null hypothesis (which is why the critical region is also sometimes called the rejection region). How do we find this critical region? Well, let’s consider what we know:

X should be very big or very small in order to reject the null hypothesis.
If the null hypothesis is true, the sampling distribution of X is Binomial(0.5,N).
If α=.05, the critical region must cover 5% of this sampling distribution.

It’s important to make sure you understand this last point: the critical region corresponds to those values of X for which we would reject the null hypothesis, and the sampling distribution in question describes the probability that we would obtain a particular value of X if the null hypothesis were actually true. Now, let’s suppose that we chose a critical region that covers 20% of the sampling distribution, and suppose that the null hypothesis is actually true. What would be the probability of incorrectly rejecting the null? The answer is of course 20%. And therefore, we would have built a test that had an α level of 0.2. If we want α=.05, the critical region is only allowed to cover 5% of the sampling distribution of our test statistic.

Figure 11.2: The critical region associated with the hypothesis test for the ESP study, for a hypothesis test with a significance level of α=.05. The plot itself shows the sampling distribution of X under the null hypothesis: the grey bars correspond to those values of X for which we would retain the null hypothesis. The black bars show the critical region: those values of X for which we would reject the null. Because the alternative hypothesis is two sided (i.e., allows both θ<.5 and θ>.5), the critical region covers both tails of the distribution. To ensure an α level of .05, we need to ensure that each of the two regions encompasses 2.5% of the sampling distribution.

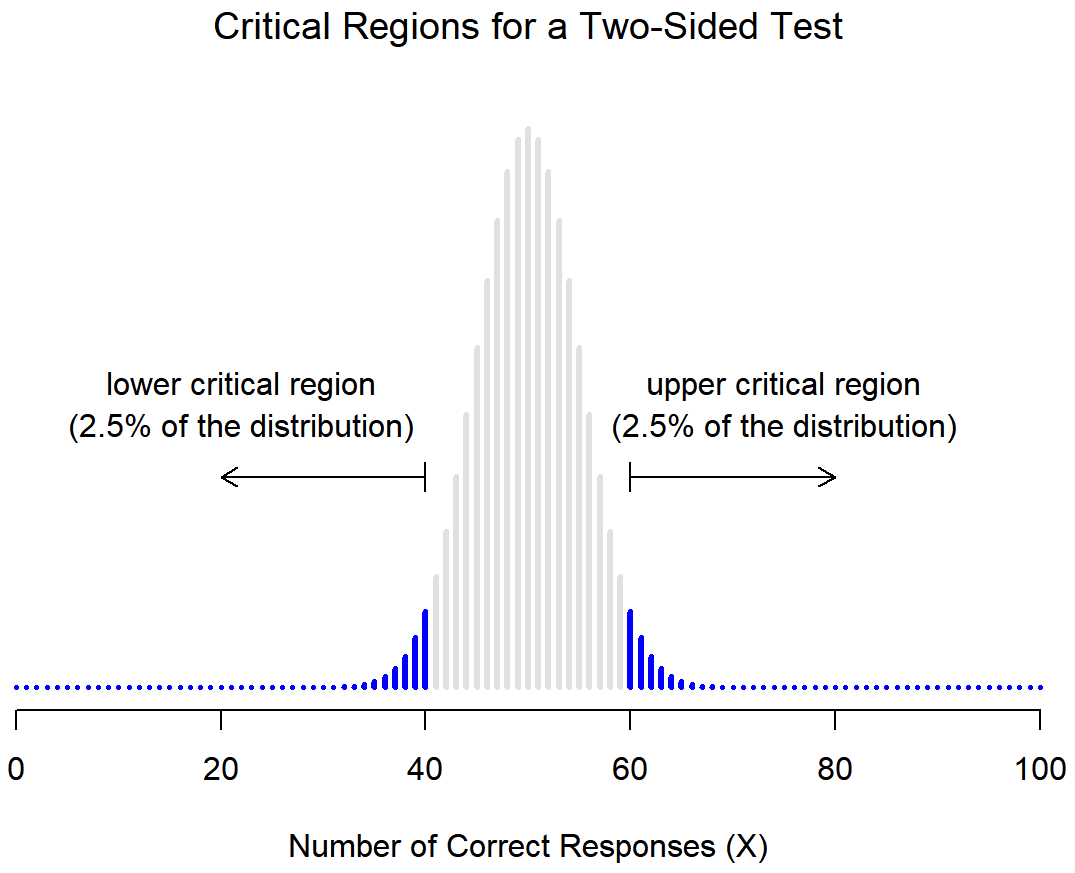
As it turns out, those three things uniquely solve the problem: our critical region consists of the most extreme values, known as the tails of the distribution. This is illustrated in Figure 11.2. As it turns out, if we want α=.05, then our critical regions correspond to X≤40 and X≥60.¹⁶¹ That is, if the number of people saying “true” is between 41 and 59, then we should retain the null hypothesis. If the number is between 0 to 40 or between 60 to 100, then we should reject the null hypothesis. The numbers 40 and 60 are often referred to as the critical values, since they define the edges of the critical region.

At this point, our hypothesis test is essentially complete: (1) we choose an α level (e.g., α=.05, (2) come up with some test statistic (e.g., X) that does a good job (in some meaningful sense) of comparing H0 to H1, (3) figure out the sampling distribution of the test statistic on the assumption that the null hypothesis is true (in this case, binomial) and then (4) calculate the critical region that produces an appropriate α level (0-40 and 60-100). All that we have to do now is calculate the value of the test statistic for the real data (e.g., X=62) and then compare it to the critical values to make our decision. Since 62 is greater than the critical value of 60, we would reject the null hypothesis. Or, to phrase it slightly differently, we say that the test has produced a significant result.

note on statistical “significance”

Like other occult techniques of divination, the statistical method has a private jargon deliberately contrived to obscure its methods from non-practitioners.

– Attributed to G. O. Ashley¹⁶²

A very brief digression is in order at this point, regarding the word “significant”. The concept of statistical significance is actually a very simple one, but has a very unfortunate name. If the data allow us to reject the null hypothesis, we say that “the result is statistically significant”, which is often shortened to “the result is significant”. This terminology is rather old, and dates back to a time when “significant” just meant something like “indicated”, rather than its modern meaning, which is much closer to “important”. As a result, a lot of modern readers get very confused when they start learning statistics, because they think that a “significant result” must be an important one. It doesn’t mean that at all. All that “statistically significant” means is that the data allowed us to reject a null hypothesis. Whether or not the result is actually important in the real world is a very different question, and depends on all sorts of other things.

difference between one sided and two sided tests

There’s one more thing I want to point out about the hypothesis test that I’ve just constructed. If we take a moment to think about the statistical hypotheses I’ve been using,

H₀:θ=.5

H₁:θ≠.5

we notice that the alternative hypothesis covers both the possibility that θ<.5 and the possibility that θ>.5. This makes sense if I really think that ESP could produce better-than-chance performance or worse-than-chance performance (and there are some people who think that). In statistical language, this is an example of a two-sided test. It’s called this because the alternative hypothesis covers the area on both “sides” of the null hypothesis, and as a consequence the critical region of the test covers both tails of the sampling distribution (2.5% on either side if α=.05), as illustrated earlier in Figure 11.2.

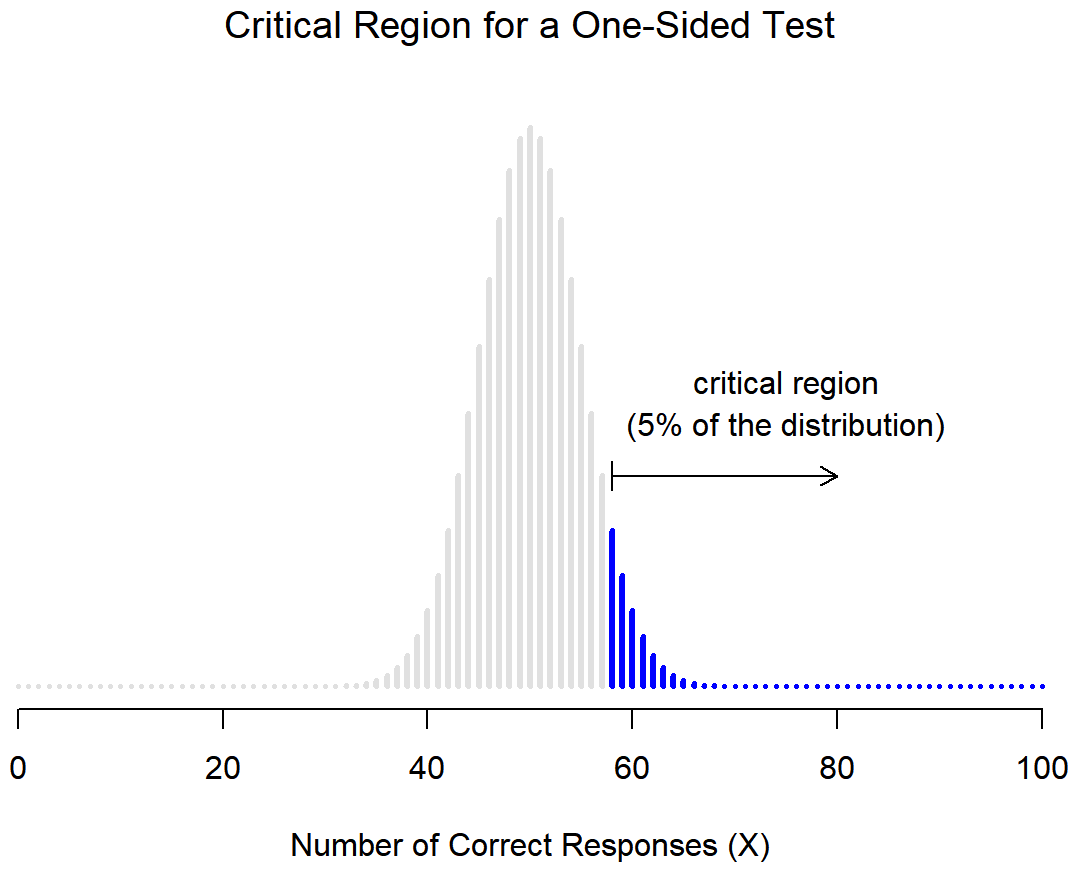
However, that’s not the only possibility. It might be the case, for example, that I’m only willing to believe in ESP if it produces better than chance performance. If so, then my alternative hypothesis would only covers the possibility that θ>.5, and as a consequence the null hypothesis now becomes θ≤.5:

H₀:θ≤.5

H₁:θ>.5

When this happens, we have what’s called a one-sided test, and when this happens the critical region only covers one tail of the sampling distribution. This is illustrated in Figure 11.3.

Figure 11.3: The critical region for a one sided test. In this case, the alternative hypothesis is that θ>.05, so we would only reject the null hypothesis for large values of X. As a consequence, the critical region only covers the upper tail of the sampling distribution; specifically the upper 5% of the distribution. Contrast this to the two-sided version earlier)