4.6: The Uniform Distribution
- Page ID
- 4569
The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to occur. When working out problems that have a uniform distribution, be careful to note if the data is inclusive or exclusive of endpoints.
The mathematical statement of the uniform distribution is
\(f(x) = \frac{1}{b-a}\) for \(a \leq x \leq b\)
where \(a =\) the lowest value of \(x\) and \(b =\) the highest value of \(x\).
Formulas for the theoretical mean and standard deviation are
\(\mu=\frac{a+b}{2}\) and \(\sigma=\sqrt{\frac{(b-a)^{2}}{12}}\)
The data that follow are the number of passengers on 35 different charter fishing boats. The sample mean = 7.9 and the sample standard deviation = 4.33. The data follow a uniform distribution where all values between and including zero and 14 are equally likely. State the values of \(a\) and \(b\). Write the distribution in proper notation, and calculate the theoretical mean and standard deviation.
| 1 | 12 | 4 | 10 | 4 | 14 | 11 |
| 7 | 11 | 4 | 13 | 2 | 4 | 6 |
| 3 | 10 | 0 | 12 | 6 | 9 | 10 |
| 5 | 13 | 4 | 10 | 14 | 12 | 11 |
| 6 | 10 | 11 | 0 | 11 | 13 | 2 |
-
Table \(\PageIndex{1}\)
The amount of time, in minutes, that a person must wait for a bus is uniformly distributed between zero and 15 minutes, inclusive.
a. What is the probability that a person waits fewer than 12.5 minutes?
- Answer
-
a. Let \(X\) = the number of minutes a person must wait for a bus. \(a = 0\) and \(b = 15\). \(X \sim U(0, 15)\). Write the probability density function. \(f(x) = \frac{1}{15-0}=\frac{1}{15}\) for \(0 \leq x \leq 15\).
Find \(P(x < 12.5)\). Draw a graph.
\[P(x<k)=\text { (base) (height) }=(12.5-0)\left(\frac{1}{15}\right)=0.8333\nonumber\]
The probability a person waits less than 12.5 minutes is 0.8333.
Figure \(\PageIndex{1}\)
b. On the average, how long must a person wait? Find the mean, \(\mu\), and the standard deviation, \(\sigma\).
- Answer
-
b. \(\mu=\frac{a+b}{2}=\frac{15+0}{2}=7.5\). On the average, a person must wait 7.5 minutes.
\(\sigma=\sqrt{\frac{(b-a)^{2}}{12}}=\sqrt{\frac{(15-\theta)^{2}}{12}}=4.3\). The Standard deviation is 4.3 minutes.
c. Ninety percent of the time, the time a person must wait falls below what value?
This asks for the 90th percentile.
- Answer
-
c. Find the 90th percentile. Draw a graph. Let \(k =\) the 90th percentile.
\(P(x<k)>
\(0.90=(k)\left(\frac{1}{15}\right)\)
\(k=(0.90)(15)=13.5\)
The 90th percentile is 13.5 minutes. Ninety percent of the time, a person must wait at most 13.5 minutes.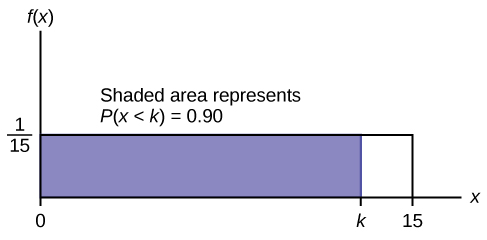 Figure \(\PageIndex{2}\)
Figure \(\PageIndex{2}\)
The total duration of baseball games in the major league in the 2011 season is uniformly distributed between 447 hours and 521 hours inclusive.
- Find \(a\) and \(b\) and describe what they represent.
- Write the distribution.
- Find the mean and the standard deviation.
- What is the probability that the duration of games for a team for the 2011 season is between 480 and 500 hours?


